Capillarity
Storyboard 
Capillarity is an effect of the attraction of the molecules to each other that generates that the surfaces of the liquids seek to minimize.
In the case of a drop this leads to the formation of approximately spherical drops and in the case of liquid in a capillary that they rise and form meniscus.
The effect of ascending through capillaries or deforming surfaces is called capillarity and depends on the surface tension parameter.
ID:(881, 0)
Capillarity in tube on surface
Definition 
The rise of the meniscus occurs due to the balance between the pressure generated by surface tension (upward) and the column of water (downward).
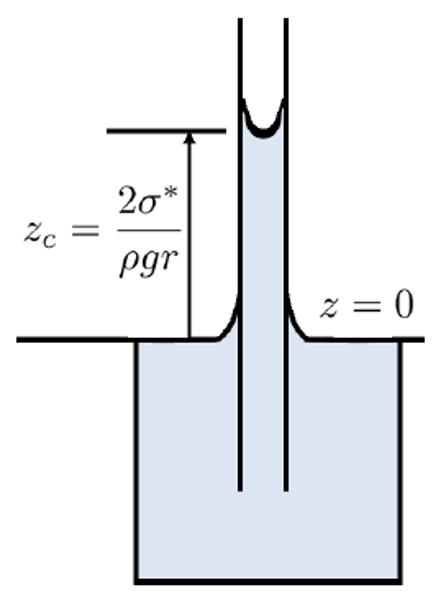
By equating these two forces, the height of the column is determined.
ID:(2983, 0)
Tube capillarity
Image 
When a very narrow tube is dipped into a liquid such as water, the meniscus is observed to rise above the level of the liquid outside the tube.
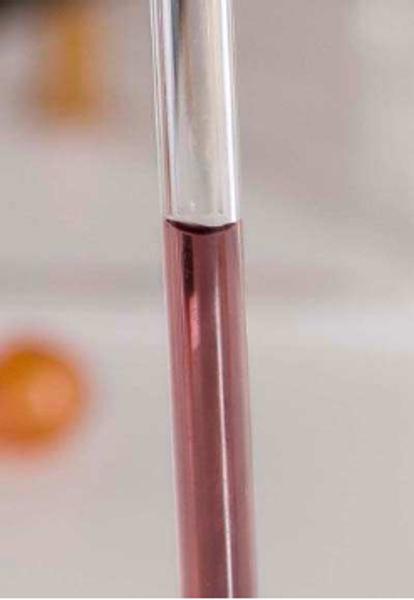
This phenomenon is known as capillarity and is one of the factors that aid in the upward movement of water through the stem of a plant.
ID:(2981, 0)
Practical surface tension
Note 
If a ring is hung from a dynamometer, its weight can be determined.
When attempting to submerge it in water, it is observed that the measured weight decreases significantly as the ring fails to penetrate the water. This is due to the surface tension, which opposes the ring's entry into the water surface. The weight is reduced by the force of the surface tension multiplied by the contact area.
Once the ring penetrates the water, the dynamometer returns to nearly the original weight. However, the weight is slightly lower as the ring experiences some buoyancy from the displaced water.
When attempting to remove the ring from the water, it can be easily extracted until the lower edge of the ring reaches the water surface. At this point, the ring starts dragging the water surface that remains adhered to its edge. The required force increases progressively as the surface area in contact grows larger. This changes abruptly when the water surface breaks, and the ring is finally released.
ID:(117, 0)
Tube capillarity equation
Quote 
The surface tension causes the meniscus to curve, forming a radius of curvature $R$, resulting in a contact angle $\theta$ between the liquid surface and the edge:

ID:(2982, 0)
Capillarity
Description 
Capillarity is an effect of the attraction of the molecules to each other that generates that the surfaces of the liquids seek to minimize. In the case of a drop this leads to the formation of approximately spherical drops and in the case of liquid in a capillary that they rise and form meniscus. The effect of ascending through capillaries or deforming surfaces is called capillarity and depends on the surface tension parameter.
Variables
Calculations
Calculations
Equations
Examples
The rise of the meniscus occurs due to the balance between the pressure generated by surface tension (upward) and the column of water (downward).

By equating these two forces, the height of the column is determined.
(ID 2983)
When a very narrow tube is dipped into a liquid such as water, the meniscus is observed to rise above the level of the liquid outside the tube.

This phenomenon is known as capillarity and is one of the factors that aid in the upward movement of water through the stem of a plant.
(ID 2981)
If a ring is hung from a dynamometer, its weight can be determined.
When attempting to submerge it in water, it is observed that the measured weight decreases significantly as the ring fails to penetrate the water. This is due to the surface tension, which opposes the ring's entry into the water surface. The weight is reduced by the force of the surface tension multiplied by the contact area.
Once the ring penetrates the water, the dynamometer returns to nearly the original weight. However, the weight is slightly lower as the ring experiences some buoyancy from the displaced water.
When attempting to remove the ring from the water, it can be easily extracted until the lower edge of the ring reaches the water surface. At this point, the ring starts dragging the water surface that remains adhered to its edge. The required force increases progressively as the surface area in contact grows larger. This changes abruptly when the water surface breaks, and the ring is finally released.
(ID 117)
The surface tension causes the meniscus to curve, forming a radius of curvature $R$, resulting in a contact angle $\theta$ between the liquid surface and the edge:

(ID 2982)
If a liquid surface with surface tension $\sigma$ exhibits a curvature with a radius of $r$, the pressure generated in the direction of the surface is given by
| $ p \equiv\displaystyle\frac{2 \sigma }{ r }$ |
.
(ID 4484)
ID:(881, 0)
