User:
Viscous laminar flow
Storyboard 
When we assume laminar flow of a viscous fluid through a tube, we observe a pattern where the velocity is highest at the center and decreases to zero at the edges. The total flow is dependent on the cylindrical profile and is inversely proportional to the viscosity of the fluid, with a fourth power relationship to the radius.
ID:(876, 0)
Mechanisms
Iframe
Mechanisms
ID:(15491, 0)
Laminar flow through a tube
Concept
When a tube filled with liquid with a viscosity of viscosity ($\eta$) is exposed to the pressure in the initial position ($p_i$) at the position at the beginning of the tube ($L_i$) and the pressure in end position (e) ($p_e$) at the position at the end of the tube ($L_e$), it generates a pressure difference ($\Delta p_s$) along the tube length ($\Delta L$), resulting in the profile of the speed on a cylinder radio ($v$):
In flows with low values of the number of Reynold ($Re$), where viscosity is more significant than the inertia of the liquid, the flow develops in a laminar manner, meaning without the presence of turbulence.
ID:(2218, 0)
Laminars in the stream
Concept
In laminar flow, adjacent layers move, and there exists a force generated by viscosity between them. The faster layer drags its slower neighbor, while the slower one restricts the advancement of the faster one.
Therefore, the force the viscose force ($F_v$) generated by ($$) over the other is a function of ($$), ($$), and ($$), as depicted in the following equation:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
illustrated in the following diagram:
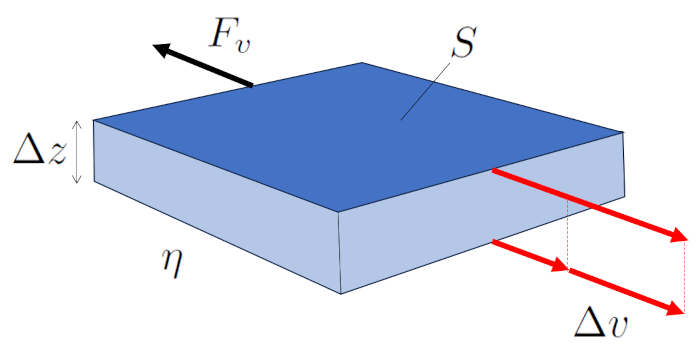
ID:(7053, 0)
Flow through a cylinder
Concept
Laminar flow around a cylinder can be represented as multiple cylindrical layers sliding under the influence of adjacent layers. In this case, the viscose force ($F_v$) with the tube length ($\Delta L$), the viscosity ($\eta$), and the variables the cylinder radial position ($r$) and the speed on a cylinder radio ($v$) is expressed as:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
The layer at the boundary at ($$) remains stationary due to the boundary effect and, through the viscosity ($\eta$), slows down the adjacent layer which does have velocity.
The center is the part moving at the maximum flow rate ($v_{max}$), dragging the surrounding layer. In turn, this layer drags the next one, and so on until reaching the layer in contact with the cylinder wall, which is stationary.
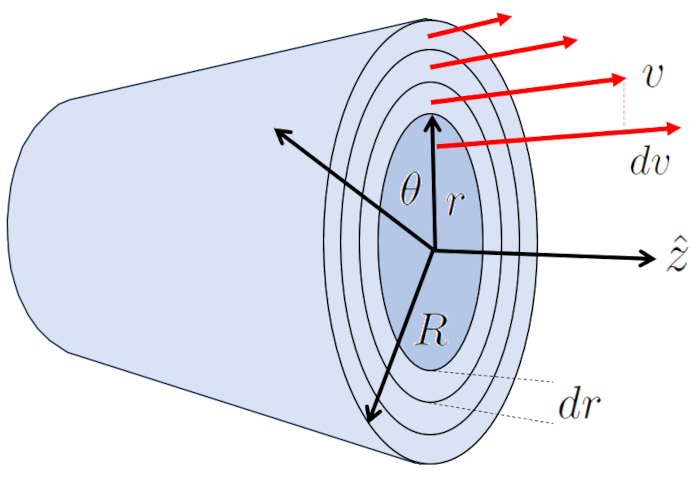
Thus, the system transfers energy from the center to the wall, generating a velocity profile represented by:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
with:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(7057, 0)
Flow for inhomogeneous flux density
Concept
In the case that the flux density ($j_s$) is constant, the volume flow ($J_V$) can be calculated using the section or Area ($S$) according to:
| $ J_V = S j_s $ |
If the flux density ($j_s$) varies, sufficiently small sectional elements $dS$ can be considered so that the equation remains valid in the sense that the contribution to flow is:
$dJ_V = j_s dS$
Integrating this expression over the entire section results in
| $ J_V =\displaystyle\int j_s dS $ |
ID:(15719, 0)
Flow after Hagen-Poiseuille equation
Concept
The profile of the speed on a cylinder radio ($v$) in the radius of position in a tube ($r$) allows us to calculate the volume flow ($J_V$) in a tube by integrating over the entire surface, which leads us to the well-known Hagen-Poiseuille law.
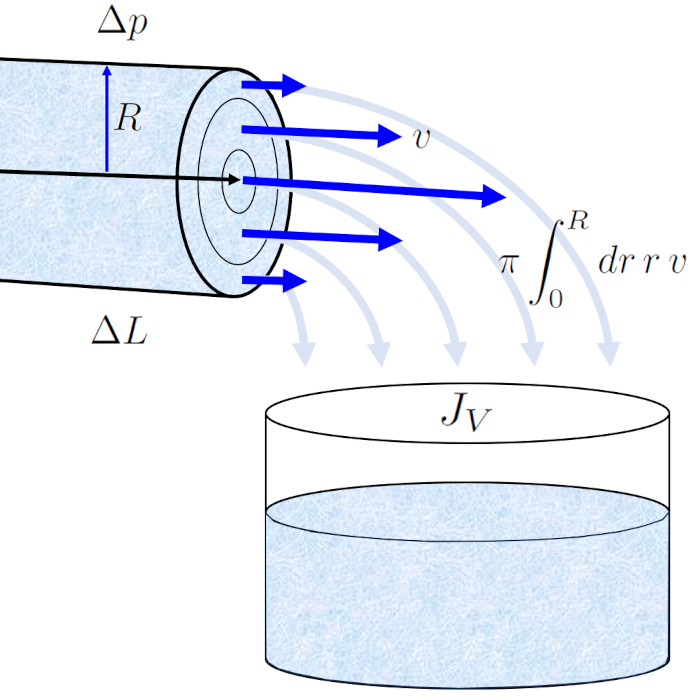
The result is an equation that depends on tube radius ($R$) raised to the fourth power. However, it is crucial to note that this flow profile only holds true in the case of laminar flow.
Thus, from the viscosity ($\eta$), it follows that the volume flow ($J_V$) before ($$) and ($$), the expression:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
The original papers that gave rise to this law with a combined name were:
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen" (On the laws governing the flow of water in cylindrical vessels), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Experimental research on the movement of liquids in tubes of very small diameters), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Reynold Number
Top
The inertia of a liquid can be understood as proportional to the density of kinetic energy, given by
$\displaystyle\frac{\rho_w}{2}v^2$
where the liquid density ($\rho_w$) and the mean Speed of Fluid ($v$).
If we consider the viscose force ($F_v$) as
$F_v=S\eta\displaystyle\frac{v}{R}$
where the section or Area ($S$), the viscosity ($\eta$), the mean Speed of Fluid ($v$), and the typical Dimension of the System ($R$) are properties of the liquid.
Let's remember that energy is equal to the viscose force ($F_v$) multiplied by the distance traveled ($l$). The density of energy lost due to viscosity will be equal to force multiplied by distance divided by volume $S l$:
$\displaystyle\frac{F_vl}{Sl}=S\eta\displaystyle\frac{v}{R}\displaystyle\frac{l}{Sl}=\eta\displaystyle\frac{v}{R}$
Therefore, the ratio between the density of kinetic energy and the density of viscous energy is equal to a dimensionless number known as the number of Reynold ($Re$). When the number of Reynold ($Re$) is much greater than one, inertia dominates over viscous force, and the flow becomes turbulent. On the other hand, if the number of Reynold ($Re$) is small, viscous force dominates, and the flow becomes laminar.
| $ Re =\displaystyle\frac{ \rho R v_{max} }{ \eta }$ |
In summary, the number of Reynold ($Re$) is a dimensionless parameter that indicates the relationship between inertia and viscous force in a flow. If the Reynolds number is much less than one ($Re\ll 1$), viscosity dominates, and the flow is laminar. If the Reynolds number is greater than one ($Re\gg 1$), inertia dominates, and the flow is turbulent.
The original paper in which Osborne Reynolds introduces the number named after him is:
"An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels", Osborne Reynolds, Philosophical Transactions of the Royal Society of London, Vol. 174, pp. 935-982 (1883).
ID:(15507, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \Delta L = L_e - L_i $
DL = L_e - L_i
$ \Delta p = p_e - p_i $
Dp = p_e - p_i
$ j_s = \displaystyle\frac{ J_V }{ S }$
j_s = J_V / S
$ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$
J_V =- pi * R ^4* Dp /(8* eta * DL )
$ Re =\displaystyle\frac{ \rho R v_{max} }{ \eta }$
Re = rho * R * v / eta
$ S = \pi R ^2$
S = pi * r ^2
$ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$
v = v_max *(1- ( r / R )^2)
$ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$
v_max = - R ^2* Dp /(4* DL * eta )
ID:(15493, 0)
Pressure difference
Equation
When the pressure in the initial position ($p_i$) and the pressure in end position (e) ($p_e$) are connected, a the pressure difference ($\Delta p_s$) is created, which is calculated using the following formula:
| $ \Delta p = p_e - p_i $ |
the pressure difference ($\Delta p_s$) represents the pressure difference that will cause the liquid to flow from the taller column to the shorter one.
ID:(14459, 0)
Change in length
Equation
To describe the flow, a coordinate system is defined in which the liquid flows from the position at the beginning of the tube ($L_i$) to the position at the end of the tube ($L_e$), indicating that the pressure at the pressure in the initial position ($p_i$) is greater than at the pressure in end position (e) ($p_e$). This movement depends on the tube length ($\Delta L$), which is calculated as follows:
| $ \Delta L = L_e - L_i $ |
ID:(3802, 0)
Speed profile of flow in a cylinder
Equation
When solving the flow equation with the boundary condition, we obtain the speed on a cylinder radio ($v$) as a function of the curvature radio ($r$), represented by a parabola centered at the maximum flow rate ($v_{max}$) and equal to zero at the tube radius ($R$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
When a the pressure difference ($\Delta p_s$) acts on a section with an area of $\pi R^2$, with the tube radius ($R$) as the curvature radio ($r$), it generates a force represented by:
$\pi r^2 \Delta p$
This force drives the liquid against viscous resistance, given by:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
By equating these two forces, we obtain:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Which leads to the equation:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
If we integrate this equation from a position defined by the curvature radio ($r$) to the edge where the tube radius ($R$) (taking into account that the velocity at the edge is zero), we can obtain the speed on a cylinder radio ($v$) as a function of the curvature radio ($r$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Where:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
is the maximum flow rate ($v_{max}$) at the center of the flow.
.
ID:(3627, 0)
Maximal speed of flow in a cylinder
Equation
The value of the maximum flow rate ($v_{max}$) at the center of a cylinder depends on the viscosity ($\eta$), the tube radius ($R$), and the gradient created by the pressure difference ($\Delta p_s$) and the tube length ($\Delta L$), as represented by:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
The negative sign indicates that the flow always occurs in the direction opposite to the gradient, meaning from the area of higher pressure to the area of lower pressure.
ID:(3628, 0)
Hagen Poiseuille Equation
Equation
The volume flow ($J_V$) can be calculated with the Hagen-Poiseuille law that with the parameters the viscosity ($\eta$), the pressure difference ($\Delta p$), the tube radius ($R$) and the tube length ($\Delta L$) is:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
If we consider the profile of speed on a cylinder radio ($v$) for a fluid in a cylindrical channel, where the speed on a cylinder radio ($v$) varies with respect to radius of position in a tube ($r$) according to the following expression:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
involving the tube radius ($R$) and the maximum flow rate ($v_{max}$). We can calculate the maximum flow rate ($v_{max}$) using the viscosity ($\eta$), the pressure difference ($\Delta p$), and the tube length ($\Delta L$) as follows:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
If we integrate the velocity across the cross-section of the channel, we obtain the volume flow ($J_V$), defined as the integral of $\pi r v(r)$ with respect to radius of position in a tube ($r$) from $0$ to tube radius ($R$). This integral can be simplified as follows:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
The integration yields the resulting Hagen-Poiseuille law:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(3178, 0)
Volume Flow and its Speed
Equation
A flux density ($j_s$) can be expressed in terms of the volume flow ($J_V$) using the section or Area ($S$) through the following formula:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Thus, the flow is a flux density ($j_s$), which is calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 0)
Reynold Number
Equation
The key criterion for determining whether a medium is laminar or turbulent is the Reynolds number, which compares the energy associated with inertia to that associated with viscosity. The former depends on the density ($\rho$), the mean Speed of Fluid ($v$), and the typical Dimension of the System ($R$), while the latter depends on the viscosity ($\eta$), defining it as:
| $ Re =\displaystyle\frac{ \rho R v_{max} }{ \eta }$ |
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Surface of a disk
Equation
The surface of a disk ($S$) of ($$) is calculated as follows:
| $ S = \pi R ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 0)