Utilisateur:
Écoulement laminaire visqueux (Hagen Poiseuille)
Storyboard 
Lorsque l'on considère l'écoulement laminaire d'un fluide visqueux à travers un tube, un motif se forme où la vitesse est maximale au centre et nulle sur les bords. Le débit total dépend du profil cylindrique et est inversement proportionnel à la viscosité du fluide, avec une relation à la quatrième puissance par rapport au rayon.
ID:(876, 0)
Écoulement laminaire visqueux
Storyboard
Lorsque l'on considère l'écoulement laminaire d'un fluide visqueux à travers un tube, un motif se forme où la vitesse est maximale au centre et nulle sur les bords. Le débit total dépend du profil cylindrique et est inversement proportionnel à la viscosité du fluide, avec une relation à la quatrième puissance par rapport au rayon.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Si nous examinons le profil de ERROR:5449,0 pour un fluide dans un canal cylindrique, o a vitesse dans un rayon du cylindre ($v$) varie en fonction de ERROR:10120,0 selon l'expression suivante :
avec le rayon du tube ($R$) et a vitesse maximal ($v_{max}$). Nous pouvons calculer a vitesse maximal ($v_{max}$) en utilisant a viscosité ($\eta$), a différence de pression ($\Delta p$), et le longueur du tube ($\Delta L$) comme suit :
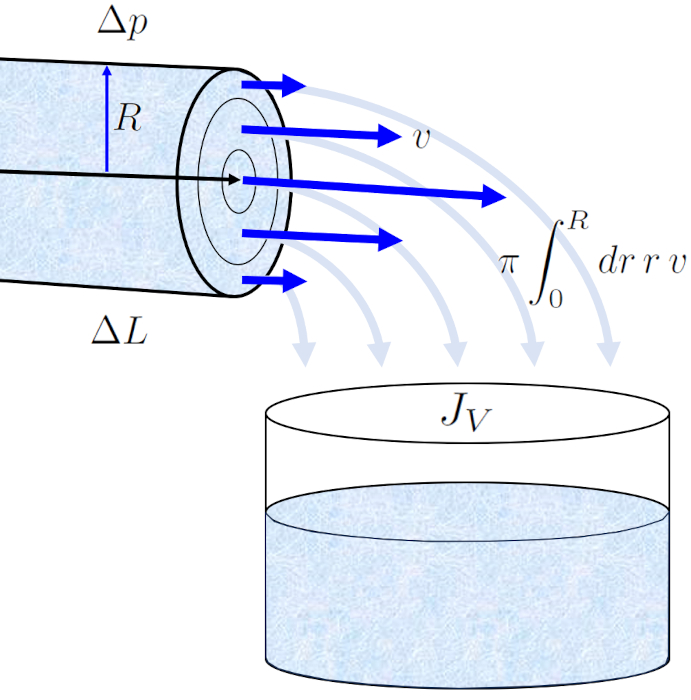
Si nous int grons la vitesse sur toute la section transversale du canal, nous obtenons le volumique flux ($J_V$), d fini comme l'int grale de $\pi r v(r)$ par rapport ERROR:10120,0 de $0$ ERROR:5417,0. Cette int grale peut tre simplifi e comme suit :
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
L'int gration donne la loi de Hagen-Poiseuille r sultante :
Quand une a différence de pression ($\Delta p_s$) agit sur une section avec une aire de $\pi R^2$, avec le rayon du tube ($R$) comme le rayon de courbure ($r$), elle g n re une force repr sent e par :
$\pi r^2 \Delta p$
Cette force pousse le liquide contre la r sistance visqueuse, donn e par :
En galant ces deux forces, nous obtenons :
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Ce qui nous conduit l' quation :
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Si nous int grons cette quation d'une position d finie par le rayon de courbure ($r$) jusqu'au bord o se trouve le rayon du tube ($R$) (en tenant compte que la vitesse au bord est nulle), nous pouvons obtenir a vitesse dans un rayon du cylindre ($v$) en fonction de le rayon de courbure ($r$) :
O :
est a vitesse maximal ($v_{max}$) au centre de l' coulement.
Le flux est d fini comme le volume le élément de volume ($\Delta V$) divis par le temps le temps écoulé ($\Delta t$), ce qui est exprim dans l' quation suivante :
et le volume est gal la section transversale a section de tube ($S$) multipli e par la distance parcourue le élément tubulaire ($\Delta s$) :
tant donn que la distance parcourue le élément tubulaire ($\Delta s$) par unit de temps le temps écoulé ($\Delta t$) correspond la vitesse, elle est repr sent e par :
Ainsi, le flux est une densité de flux ($j_s$), qui est calcul l'aide de :
Exemples
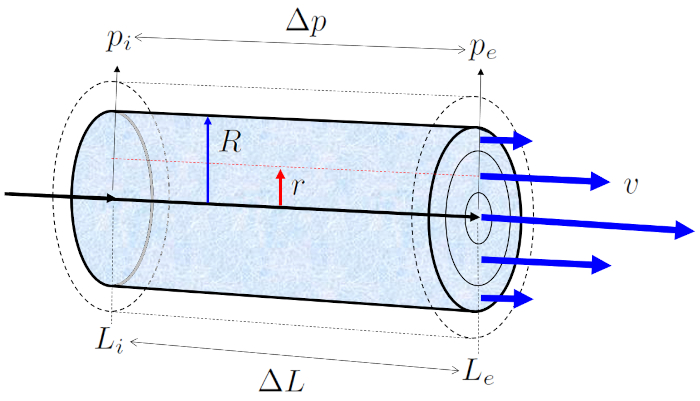
Lorsqu'un tube rempli de liquide d'une viscosit de ERROR:5422,0 est expos a pression en position initiale ($p_i$) en le positionner au début du tube ($L_i$) et a pression en position finale (e) ($p_e$) en le positionner au bout du tube ($L_e$), cela g n re une différence de pression ($\Delta p_s$) le long de le longueur du tube ($\Delta L$), ce qui donne le profil de a vitesse dans un rayon du cylindre ($v$) :
Dans les coulements avec de faibles valeurs de le le numéro de Reynold ($Re$), o la viscosit est plus significative que l'inertie du liquide, l' coulement se d veloppe de mani re lamin e, c'est- -dire sans la pr sence de turbulences.
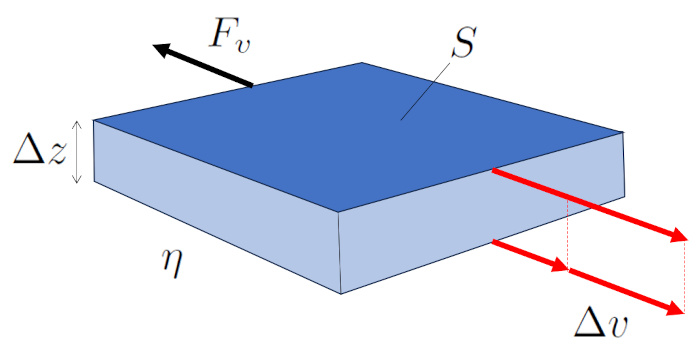
Dans un coulement laminaire, des couches adjacentes se d placent et une force est g n r e par la viscosit entre elles. La couche la plus rapide entra ne sa voisine plus lente, tandis que la plus lente limite l'avancement de la plus rapide.
Par cons quent, la force a force visqueuse ($F_v$) g n r e par ERROR:10119.1 sur l'autre est une fonction de ERROR:5556.1, ERROR:5436.1 et ERROR:5422.1, comme indiqu dans l' quation suivante :
illustr e dans le sch ma suivant :
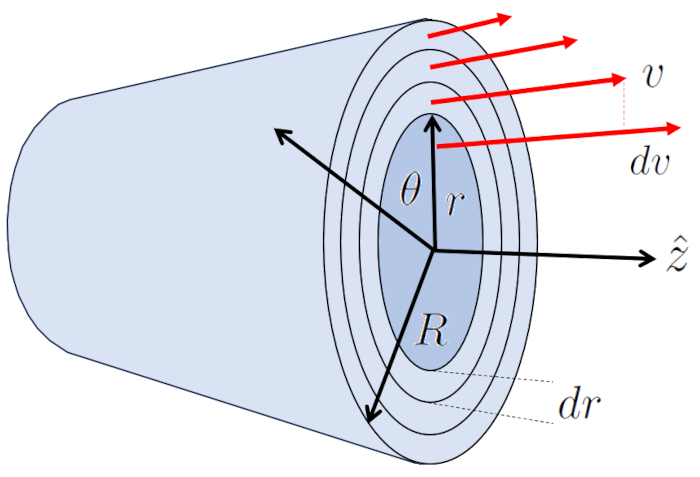
L' coulement laminaire autour d'un cylindre peut tre repr sent comme plusieurs couches cylindriques glissant sous l'influence des couches adjacentes. Dans ce cas, a force visqueuse ($F_v$) avec le longueur du tube ($\Delta L$), a viscosité ($\eta$) et les variables a position radiale dans le cylindre ($r$) et a vitesse dans un rayon du cylindre ($v$) est exprim e comme suit :
La couche la fronti re ERROR:5417.1 reste stationnaire en raison de l'effet de bord et, travers a viscosité ($\eta$), ralentit la couche adjacente qui a une vitesse.
Le centre est la partie qui se d place a vitesse maximal ($v_{max}$), entra nant la couche environnante. son tour, cette couche entra ne la suivante, et ainsi de suite jusqu' ce qu'elle atteigne la couche en contact avec la paroi du cylindre, qui est immobile.
Ainsi, le syst me transf re de l' nergie du centre vers la paroi, g n rant un profil de vitesse repr sent par :
avec :
Dans le cas o a densité de flux ($j_s$) est constant, le volumique flux ($J_V$) peut tre calcul en utilisant a coupe ou surface ($S$) selon :
Si a densité de flux ($j_s$) varie, des l ments de section $dS$ suffisamment petits peuvent tre consid r s pour que l' quation reste valide, au sens o la contribution au flux est :
$dJ_V = j_s dS$
En int grant cette expression sur toute la section, on obtient que
Le profil de a vitesse dans un rayon du cylindre ($v$) en le rayon de position dans un tube ($r$) nous permet de calculer le volumique flux ($J_V$) dans un tube en int grant sur toute la surface, ce qui nous conduit la loi bien connue de Hagen-Poiseuille.
Le r sultat est une quation qui d pend de ERROR:5417,0 lev la quatri me puissance. Cependant, il est essentiel de noter que ce profil d' coulement n'est valable que dans le cas d'un coulement laminaire.
Ainsi, avec cela, on d duit de a viscosité ($\eta$) que le volumique flux ($J_V$) devant un longueur du tube ($\Delta L$) et ERROR:6673,1, l'expression :
Les articles originaux qui ont donn naissance cette loi avec un nom combin taient:
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen" (Sur les lois r gissant l' coulement de l'eau dans des r cipients cylindriques), Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres", Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
L'inertie d'un liquide peut tre comprise comme tant proportionnelle la densit d' nergie cin tique, donn e par
$\displaystyle\frac{\rho_w}{2}v^2$
o a densité du liquide ($\rho_w$) et a vitesse moyenne du fluide ($v$) sont impliqu s.
Si nous consid rons a force visqueuse ($F_v$) comme tant
$F_v=S\eta\displaystyle\frac{v}{R}$
o a coupe ou surface ($S$), a viscosité ($\eta$), a vitesse moyenne du fluide ($v$) et a dimension typique du système ($R$) sont des propri t s du liquide.
Rappelons que l' nergie est gale a force visqueuse ($F_v$) multipli e par le distance parcourue ($l$). La densit d' nergie perdue en raison de la viscosit sera gale la force multipli e par la distance divis e par le volume $S l$ :
$\displaystyle\frac{F_vl}{Sl}=S\eta\displaystyle\frac{v}{R}\displaystyle\frac{l}{Sl}=\eta\displaystyle\frac{v}{R}$
Par cons quent, le rapport entre la densit d' nergie cin tique et la densit d' nergie visqueuse est gal un nombre sans dimension connu sous le nom de le le numéro de Reynold ($Re$). Lorsque le le numéro de Reynold ($Re$) est bien sup rieur un, l'inertie l'emporte sur la force visqueuse et l' coulement devient turbulent. En revanche, si le le numéro de Reynold ($Re$) est faible, la force visqueuse domine et l' coulement devient laminaire.
En r sum , le le numéro de Reynold ($Re$) est un param tre sans dimension qui indique la relation entre l'inertie et la force visqueuse dans un coulement. Si le nombre de Reynolds est bien inf rieur un ($Re\ll 1$), la viscosit domine et l' coulement est laminaire. Si le nombre de Reynolds est sup rieur un ($Re\gg 1$), l'inertie domine et l' coulement est turbulent.
L'article original dans lequel Osborne Reynolds introduit le nombre qui porte son nom est :
"Enqu te Exp rimentale sur les Circonstances Qui D terminent Si le Mouvement de l'Eau Doit tre Direct ou Sinueux, et sur la Loi de la R sistance dans les Canaux Parall les" (An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels), Osborne Reynolds, Philosophical Transactions of the Royal Society of London, Vol. 174, pp. 935-982 (1883).
Lorsque a pression en position initiale ($p_i$) et a pression en position finale (e) ($p_e$) sont connect s, une a différence de pression ($\Delta p_s$) est cr e, qui est calcul e l'aide de la formule suivante :
a différence de pression ($\Delta p_s$) repr sente la diff rence de pression qui fera couler le liquide de la colonne la plus haute vers la colonne la plus basse.
Pour d crire l' coulement, un syst me de coordonn es est d fini dans lequel le liquide s' coule de le positionner au début du tube ($L_i$) Le positionner au bout du tube ($L_e$), ce qui signifie que la pression en a pression en position initiale ($p_i$) est sup rieure celle en a pression en position finale (e) ($p_e$). Ce mouvement d pend de le longueur du tube ($\Delta L$), qui est calcul comme suit :
En r solvant l' quation de flux avec la condition aux limites, nous obtenons a vitesse dans un rayon du cylindre ($v$) comme une fonction de le rayon de courbure ($r$), repr sent e par une parabole centr e sur a vitesse maximal ($v_{max}$) et gale z ro en le rayon du tube ($R$) :
La valeur de a vitesse maximal ($v_{max}$) au centre d'un cylindre d pend de a viscosité ($\eta$), le rayon du tube ($R$) et du gradient cr par a différence de pression ($\Delta p_s$) et le longueur du tube ($\Delta L$), comme repr sent ci-dessous :
Le signe n gatif indique que le flux s'effectue toujours dans la direction oppos e au gradient, c'est- -dire, de la zone de plus haute pression vers la zone de plus basse pression.
Le volumique flux ($J_V$) peut tre calcul avec la loi de Hagen-Poiseuille qui avec les param tres a viscosité ($\eta$), a différence de pression ($\Delta p$), le rayon du tube ($R$) et le longueur du tube ($\Delta L$) estxa0:
Une densité de flux ($j_s$) peut tre exprim en termes de le volumique flux ($J_V$) l'aide de a coupe ou surface ($S$) par la formule suivante :
Le crit re cl pour d terminer si un milieu est lamin ou turbulent est le num ro de Reynolds, qui compare l' nergie associ e l'inertie celle associ e la viscosit . La premi re d pend de a densité ($\rho$), a vitesse moyenne du fluide ($v$) et a dimension typique du système ($R$), tandis que la seconde d pend de a viscosité ($\eta$), le d finissant ainsi :
A section ($S$) de un rayon du disque ($r$) est calcul e comme suit :
ID:(876, 0)
