Storyboard

It is considered a column with water with a hole in its lower part. The emptying is monitored obtaining an output speed depending on the height of the column.

If the data is modeled with Bernoulli but the exit through the hole is modeled with Hagen Poiseville, which corrects the problem of the case in which it was assumed without viscosity.

>Model

ID:(1428, 0)

Definition

ID:(15492, 0)

Image

If a small sphere with radius $a$ is dropped into a medium with viscosity $\eta$, it will accelerate until the gravitational force,

$mg=\displaystyle\frac{4\pi}{3}a^3\rho_sg$

where $\rho_s$ is the density of the sphere material, is equal to the viscous force,

$6\pi \eta a v$

where $v$ is the velocity.

Hence, it is possible to estimate the viscosity by measuring the velocity, since

$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$

where the radius can be directly measured.

Here you can observe the behavior of the sphere:

ID:(9871, 0)

Note

This means that as the column empties and the height $h$ decreases, the velocity $v$ also decreases proportionally.

The key parameters are:

• Inner diameter of the vessel: 93 mm

• Inner diameter of the evacuation channel: 3 mm

• Length of the evacuation channel: 18 mm

These parameters are important to understand and analyze the process of column emptying and how the exit velocity varies with height.

ID:(9870, 0)

Quote

If we analyze the equation



which describes the application of Hagen-Poiseuille, we observe that the curve only matches the experimental data under the following conditions:

The velocity is low (when the column is nearly empty).

The radius of the evacuation channel must be reduced from 1.5 mm to 0.6 mm.

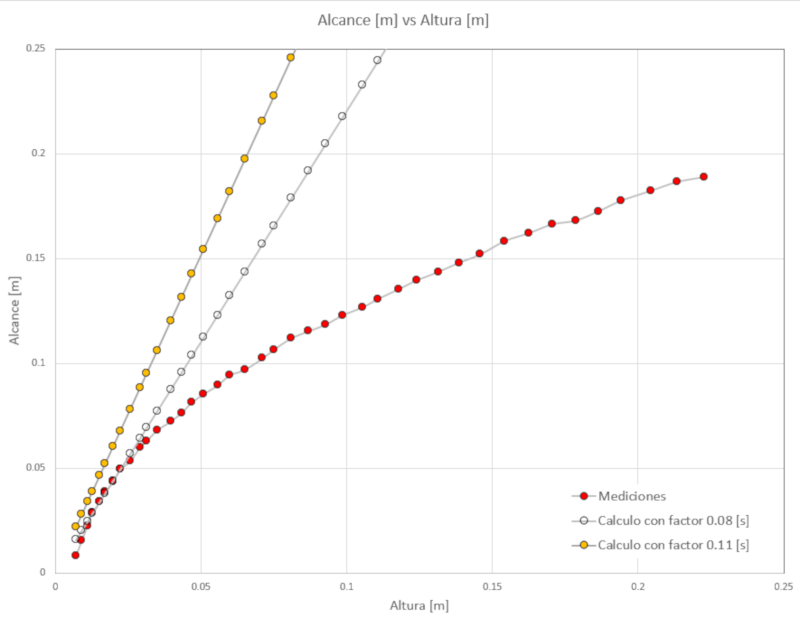
This shows that the flow is primarily turbulent and that only at low velocity levels is the velocity low enough for the Reynolds number to be low and the flow to be laminar.

ID:(11065, 0)

Exercise

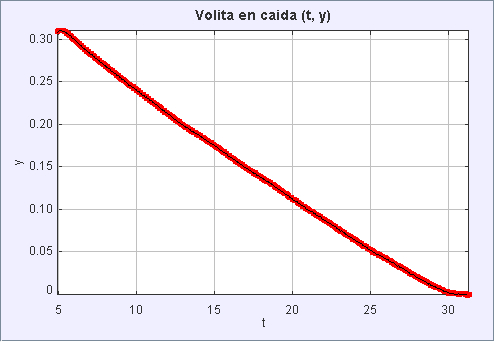
If we observe the path that the little ball takes over time, we can see that it mostly moves at a constant speed of about 0.31 meters in 25 seconds, which is equivalent to 0.0124 m/s.

By rearranging the equality between the gravitational force and the Stokes' resistance force:

$\displaystyle\frac{4\pi}{3}a^3\rho_sg =6\pi \eta a v$

we obtain:

$\eta = \displaystyle\frac{2 a^2\rho_sg}{9 v}$

Considering that the ball has a radius of 2 mm and weighs 8 mg, we can determine its density to be approximately $\rho_s\sim 2.38 g/cm^3$. Therefore, the viscosity is estimated to be around $\eta\sim 1.67, Pa s$.

ID:(9881, 0)

Equation

ID:(15494, 0)

Script

Let's consider the system of a cylindrical bucket with a drainage hole. When the plug is removed, the water starts to flow due to the existing pressure. According to Bernoulli's principle, inside the bucket ($v\sim 0$), the velocity is zero, and we have:

$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \rho g h$

while outside the bucket ($h=0$), only the kinetic component exists:

$\displaystyle\frac{1}{2}\rho v^2 + \rho g h\sim \displaystyle\frac{1}{2}\rho v^2$

Since both expressions are equal, we have:

$\displaystyle\frac{1}{2}\rho v^2=\rho g h$

which gives the velocity as:

$v=\sqrt{2 g h}$

To compare with the experiment, we can use this expression to estimate, with:



the range that the stream should have. If we plot it graphically, we observe:

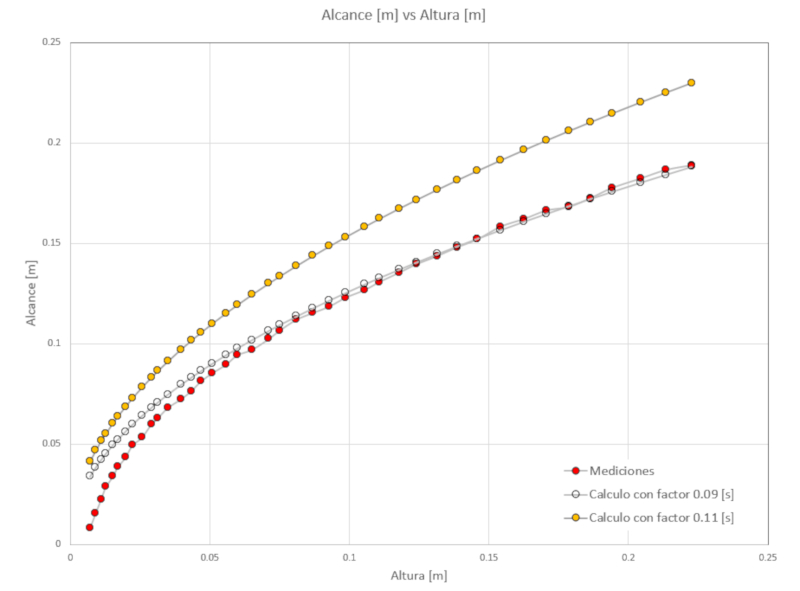
where:

• the red dots correspond to the experimental measurements,

• the blue dots correspond to the calculated range using a factor of 0.11,

• the transparent dots correspond to the calculated range using a factor of 0.09.

Therefore, we can conclude that Bernoulli\'s model overestimates the velocity at which the bucket empties. This is because in the vicinity of the drainage hole, the effects of viscosity are not negligible, and therefore, the velocity is lower.

ID:(11063, 0)