Usuario:
Dinámica de Partículas
Storyboard 
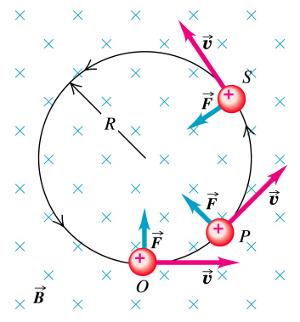
Cargas eléctricas que mueven en un campo magnético son desflecadas en forma perpendicular a la dirección en que se desplazan y en que apunta el campo magnético.
La fuerza que actúa sobre la partícula depende de la carga, de la velocidad y del campo magnético se denomina la fuerza de Lorentz.
ID:(818, 0)
Dinámica de Partículas
Descripción
Cargas eléctricas que mueven en un campo magnético son desflecadas en forma perpendicular a la dirección en que se desplazan y en que apunta el campo magnético. La fuerza que actúa sobre la partícula depende de la carga, de la velocidad y del campo magnético se denomina la fuerza de Lorentz.
Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\theta$
theta
Angulo entre velocidad y campo magnético
rad
$q$
q
Carga de prueba
C
$B$
B
Densidad de flujo magnético
T
$F$
F
Fuerza
N
$m$
m
Masa de la partícula
kg
$r$
r
Radio
m
$r$
r
Radio de giro de partícula en campo magnético
m
$v$
v
Velocidad
m/s
$\omega$
omega
Velocidad angular
rad/s
$v$
v
Velocidad de la partícula
m/s
Cálculos
Primero, seleccione la ecuación: 
a 
,
luego, seleccione la variable: 
a 
a ,
luego, seleccione la variable:
a
Símbolo
Ecuación
Resuelto
Traducido
Cálculos
Símbolo
Ecuación
Resuelto
Traducido
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
(ID 16053)
(ID 16054)
ID:(818, 0)