Efectos relativistas
Storyboard 
A velocidades cercanas a la velocidad de la luz ocurren efectos relativistas, es decir los parámetros que se miden en un sistema que viaja a una velocidad dada arrojan resultados distintos a los que se miden en un sistema en reposo. En particular los largos de los objetos se reducen y los intervalos de tiempo se alargan mientras que la masa aumenta. Sin embargo la carga de los cuerpos no es afectada.
ID:(1587, 0)
Campo eléctrico en un sistema en reposo
Definición 
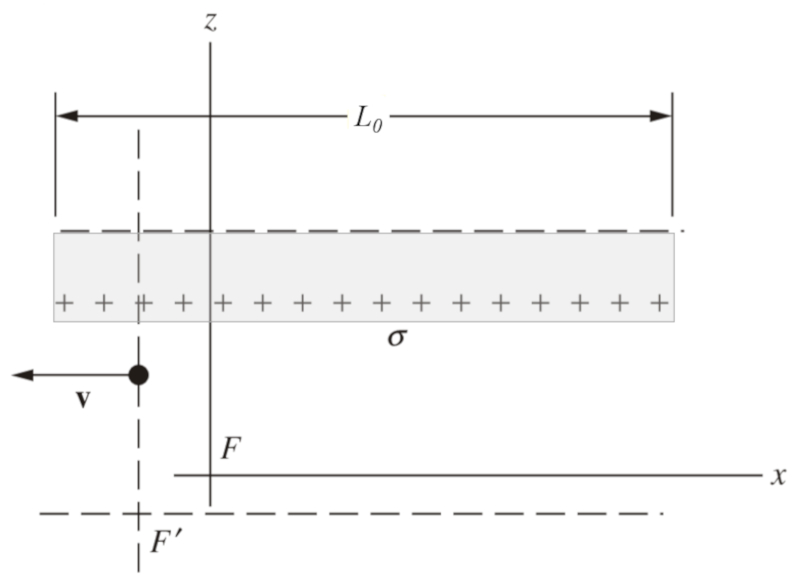
En el caso de un sistema de placas en movimiento en la dirección horizontal, el campo eléctrico dependerá de la densidad superficial de cargas en las placas:
ID:(11787, 0)
Campo eléctrico en un sistema en movimiento
Imagen 
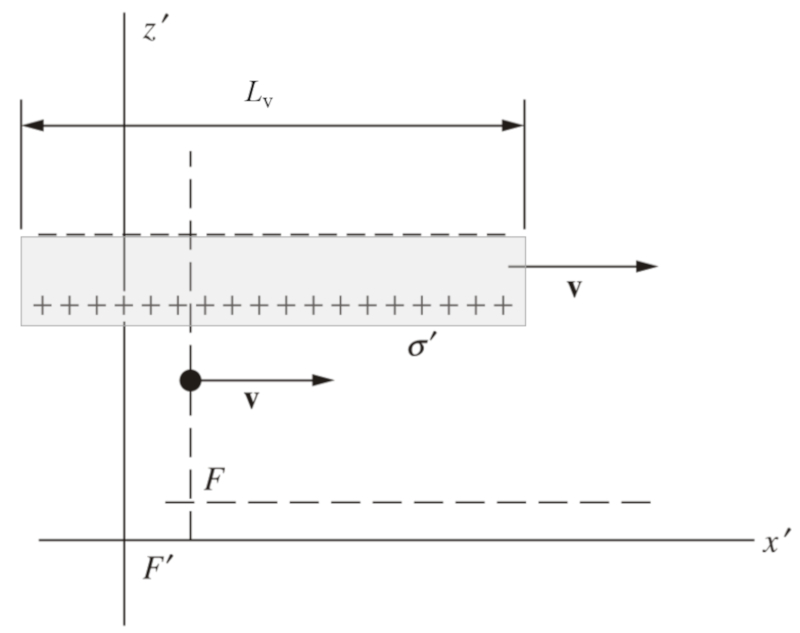
Si las placas se encuentran en movimiento, su longitud horizontal se contraerá debido a los efectos de la relatividad. Aunque las cargas no se ven afectadas por el movimiento, la concentración de carga por unidad de área aumentará a medida que las placas se contraigan. Este aumento en la concentración de carga por área resultará en un incremento en el campo eléctrico entre las placas:
ID:(11788, 0)
Argumentó para la independencia de la carga del movimiento
Nota 
En la ley de Gauss, la elección de la superficie alrededor de la carga es arbitraria. Esto significa que, ante un movimiento de una carga, siempre se puede encontrar una superficie de Gauss tal que su integral no varíe. De acuerdo con esta ley, esto implica que la carga en sí tampoco cambiará su valor:
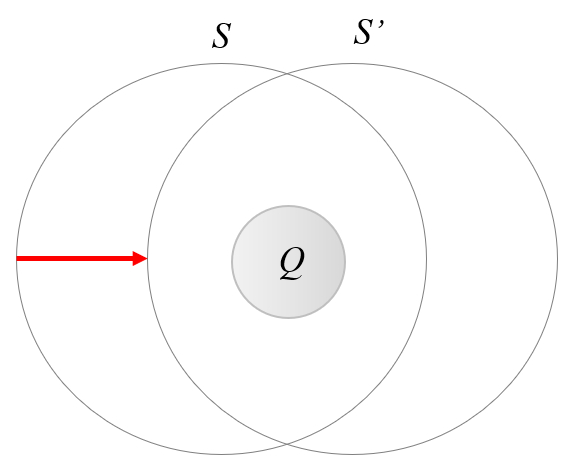
Por lo tanto:
Las cargas eléctricas son independientes de la velocidad a la que se desplace el sistema.
ID:(11793, 0)
Gedankenexperiment sobre masa y carga
Cita 
Un 'Gedankenexperiment' (experimento mental) que se puede llevar a cabo es imaginar una caja con dos cargas fijadas en un brazo que gira. La teoría de la relatividad implica que debido al movimiento, su masa aumentará. Si colgamos esta caja de un dinamómetro (una especie de balanza de mercado), este se extenderá, indicando un mayor peso. Sin embargo, el campo eléctrico medido fuera de la caja no habrá variado:
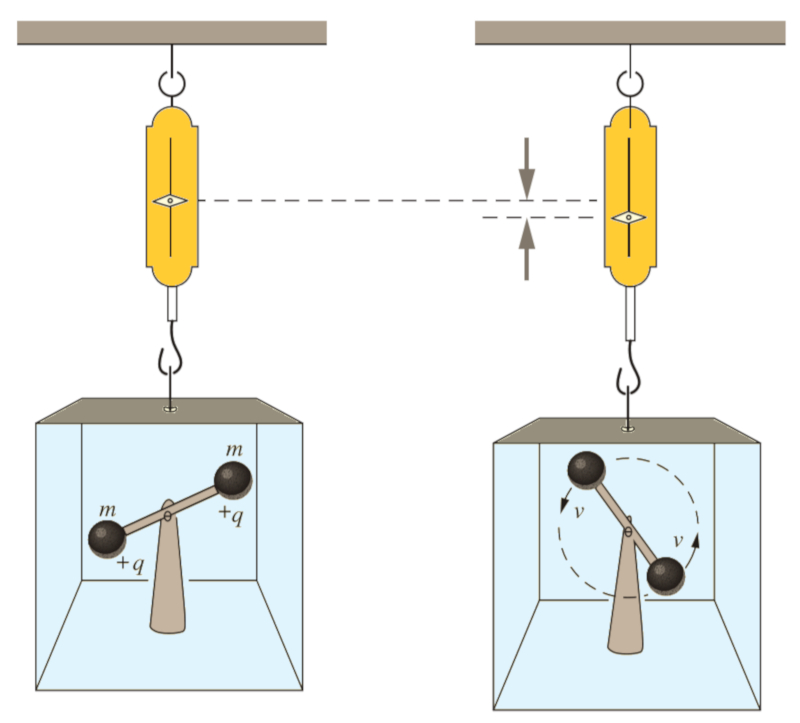
El concepto de 'Gedankenexperiment' (experimento mental) fue introducido por Einstein para facilitar la deducción de las diferentes leyes de la relatividad especial.
ID:(11794, 0)
Efectos relativistas
Descripción 
A velocidades cercanas a la velocidad de la luz ocurren efectos relativistas, es decir los parámetros que se miden en un sistema que viaja a una velocidad dada arrojan resultados distintos a los que se miden en un sistema en reposo. En particular los largos de los objetos se reducen y los intervalos de tiempo se alargan mientras que la masa aumenta. Sin embargo la carga de los cuerpos no es afectada.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
En el caso de un sistema de placas en movimiento en la direcci n horizontal, el campo el ctrico depender de la densidad superficial de cargas en las placas:

(ID 11787)
Si las placas se encuentran en movimiento, su longitud horizontal se contraer debido a los efectos de la relatividad. Aunque las cargas no se ven afectadas por el movimiento, la concentraci n de carga por unidad de rea aumentar a medida que las placas se contraigan. Este aumento en la concentraci n de carga por rea resultar en un incremento en el campo el ctrico entre las placas:

(ID 11788)
En la ley de Gauss, la elecci n de la superficie alrededor de la carga es arbitraria. Esto significa que, ante un movimiento de una carga, siempre se puede encontrar una superficie de Gauss tal que su integral no var e. De acuerdo con esta ley, esto implica que la carga en s tampoco cambiar su valor:

Por lo tanto:
Las cargas el ctricas son independientes de la velocidad a la que se desplace el sistema.
(ID 11793)
Dado que la densidad de carga est definida como:
| $ \sigma = \displaystyle\frac{ Q }{ S }$ |
y la secci n transversal $S$ se contrae en la direcci n del movimiento de acuerdo con:
| $ L_v = \displaystyle\frac{1}{ \gamma } L_0 $ |
podemos calcular la densidad de carga relativa como:
| $ \sigma_v = \gamma \sigma_0 $ |
Es importante destacar que esta relaci n es v lida nicamente si la carga no var a con el movimiento del sistema.
(ID 11789)
Como el campo el ctrico entre dos placas se describe mediante las ecuaciones:
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
En el caso relativista, la densidad de carga por rea est representada por la siguiente ecuaci n:
| $ \sigma_v = \gamma \sigma_0 $ |
Por lo tanto, podemos concluir que el campo el ctrico experimenta un aumento en su magnitud dado por la expresi n:
| $ E_{d,v} = \gamma E_{d,0} $ |
(ID 11790)
Dado que la fuerza experimentada por una carga de prueba se describe por:
| $ F = q E $ |
y la segunda ley de Newton en su forma general (en t rminos del momento $p$ en lugar de la aceleraci n) se expresa como:
| $ F =\displaystyle\frac{ dp }{ dt }$ |
podemos deducir que la ecuaci n de movimiento en un sistema en reposo es:
| $ \displaystyle\frac{dp}{dt} = q E $ |
(ID 11791)
En el contexto de la relatividad especial, el campo el ctrico se describe como:
| $ E_{d,v} = \gamma E_{d,0} $ |
junto con la ecuaci n de movimiento:
| $ \displaystyle\frac{dp}{dt} = q E $ |
y la definici n del momento:
| $ p = m_i v $ |
Esto implica que para que la din mica sea invariante bajo transformaciones relativistas, la masa debe depender de la velocidad del sistema de la siguiente manera:
| $ m_v = \gamma m_0 $ |
(ID 11792)
Un 'Gedankenexperiment' (experimento mental) que se puede llevar a cabo es imaginar una caja con dos cargas fijadas en un brazo que gira. La teor a de la relatividad implica que debido al movimiento, su masa aumentar . Si colgamos esta caja de un dinam metro (una especie de balanza de mercado), este se extender , indicando un mayor peso. Sin embargo, el campo el ctrico medido fuera de la caja no habr variado:

El concepto de 'Gedankenexperiment' (experimento mental) fue introducido por Einstein para facilitar la deducci n de las diferentes leyes de la relatividad especial.
(ID 11794)
ID:(1587, 0)
