Usuario: 
Bases de la relatividad especial
Storyboard 
El comportamiento de las partículas a velocidades próximas a la velocidad de la luz es distinta a lo que conocemos de la mecánica clásica. Por ello debemos introducir los fundamentos de la llamada relatividad especial que formulo Einstein a principios del siglo pasado.
ID:(1590, 0)
Dilatación temporal: sistema en reposo
Imagen
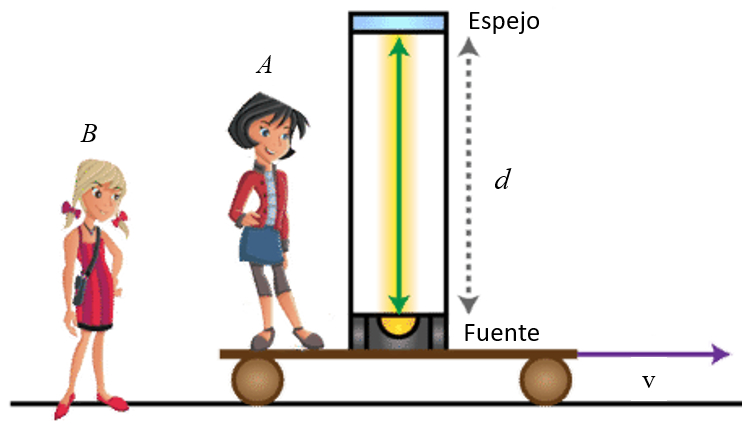
Imaginemos un sistema A que se desplaza horizontalmente a una velocidad $v$, y en este sistema tenemos un dispositivo que emite luz de forma vertical. Esta luz, después de ser reflejada en un espejo, vuelve a la fuente:
ID:(11777, 0)
Dilatación temporal: tiempo en reposo
Ecuación
Supongamos que un fotón es emitido y medimos el tiempo que tarda en ir desde la fuente hasta el espejo, lo llamamos $\Delta t_0$. Si la longitud del instrumento es $d$ y la velocidad de la luz es $c$, entonces el tiempo de ida y vuelta es:
 $ \Delta t_0 =\displaystyle\frac{ d }{ c }$ |
ID:(11778, 0)
Dilatación temporal: tiempo en movimiento
Imagen
Para el sistema A, el tiempo que se tarda en recorrer la distancia $d$ es igual a $\Delta t_0$, independientemente de si el sistema A se encuentra en movimiento a una velocidad constante $v$:
Esto se debe a que el concepto de movimiento es relativo y siempre debe referirse a una velocidad con respecto a un sistema particular. En este caso, el sistema B observa al sistema A y afirma que A se está desplazando a una velocidad $v$. Sin embargo, desde la perspectiva de A, se podría afirmar igualmente que A está en reposo y que es el sistema B el que se está desplazando a una velocidad $-v$.
ID:(11779, 0)
Dilatación temporal: desde un sistema en reposo
Imagen
Cuando se observa desde un sistema B que está en reposo en relación con el sistema A, se estima el tiempo como $\Delta t_v$:
Desde la perspectiva de B, el camino que recorre el fotón no solo incluye la distancia vertical $d$, sino también un trayecto horizontal adicional de $v \Delta t_v$.
ID:(11780, 0)
Dilatación temporal: tiempo desde un sistema en reposo
Ecuación
Desde el sistema B, la distancia recorrida se puede calcular utilizando el teorema de Pitágoras, considerando el camino horizontal recorrido $v \Delta t_v$ y el camino vertical $d$:
$(v \Delta t_v)^2+d^2=(c \Delta t_v)^2$
De esta manera, el tiempo desde el punto de vista de B se calcula como:
| $ \Delta t_v =\displaystyle\frac{ d }{\sqrt{ c ^2 - v ^2}}$ |
ID:(11781, 0)
Dilatación temporal
Ecuación
Dado que la distancia $d$ es ortogonal al desplazamiento, es independiente del desplazamiento horizontal, por lo que es igual en los tiempos de A:
| $ \Delta t_0 =\displaystyle\frac{ d }{ c }$ |
y B:
| $ \Delta t_v =\displaystyle\frac{ d }{\sqrt{ c ^2 - v ^2}}$ |
Por lo tanto, se sigue que:
| $ \Delta t_v =\displaystyle\frac{ \Delta t_0 }{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
De esto se concluye que un mismo evento tiene una duración diferente según se observe desde un sistema en el que el evento está en reposo y uno en el que se está desplazando.
Este fenómeno ilustra la relatividad del tiempo, donde el tiempo percibido varía según la velocidad relativa entre observadores.
ID:(11782, 0)
Dilatación temporal con el factor de Lorentz
Ecuación
La dilatación temporal, calculada mediante la ecuación
| $ \Delta t_v =\displaystyle\frac{ \Delta t_0 }{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
puede ser expresada de manera equivalente como
| $ \gamma =\displaystyle\frac{1}{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
de la siguiente forma:
| $ \Delta t_v = \gamma \Delta t_0 $ |
ID:(11784, 0)
Contracción de distancias
Imagen
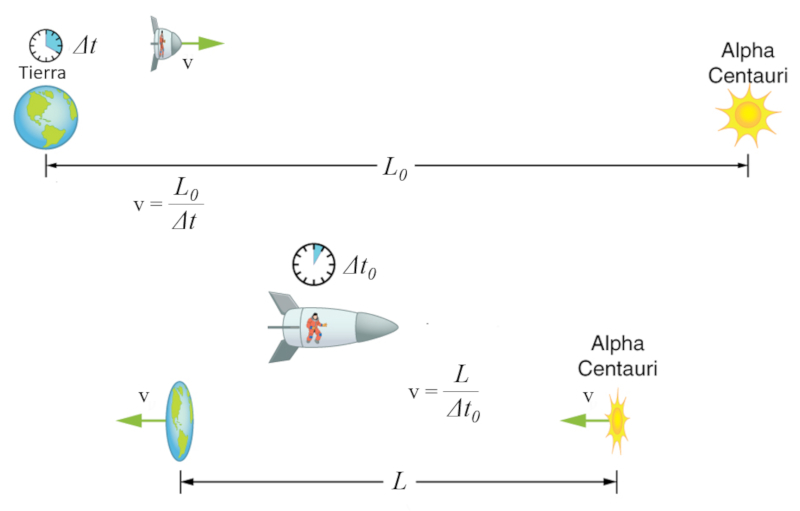
La dilatación del tiempo, junto con la restricción de que en todos los sistemas la luz tiene la misma velocidad, conduce a la necesidad de una contracción de la distancia.
ID:(11785, 0)
Contracción de distancias, relación
Ecuación
En el sistema B, la distancia recorrida por el sistema en movimiento A es igual a $L_0$ con una velocidad dada por:
$v=\displaystyle\frac{ L_0 }{ \Delta t_v }$
Desde la perspectiva del sistema A, la distancia recorrida es $L_v$ en un intervalo de tiempo $\Delta t_0$ con una velocidad dada por:
$v=\displaystyle\frac{ L_v }{ \Delta t_0 }$
Por lo tanto, con la dilatación del tiempo descrita como
| $ \Delta t_v = \gamma \Delta t_0 $ |
observamos una contracción espacial como
| $ L_v = \displaystyle\frac{1}{ \gamma } L_0 $ |
ID:(11786, 0)