Utilizador:
Lei de Faraday e campo magnético
Descrição 
Variáveis
Símbolo
Texto
Variáve
Valor
Unidades
Calcular
Valeur MKS
Unidades MKS
$\vec{H}$
&H
Campo magnético, vetor
V/m
$q$
q
Carga de teste
C
$L$
L
Comprimento do conductor
m
$\mu_0$
mu_0
Constante de campo magnético
kg m/C^2
$I$
I
Corrente
A
$\vec{B}$
&B
Densidade de fluxo magnético (vetor)
T
$B$
B
Densidade do fluxo magnético
T
$\Delta\varphi$
Dphi
Diferença potencial
V
$d\vec{H}$
d&H
Elemento de campo magnético (vetor)
V/m
$d\vec{s}$
d&s
Elemento de comprimento (vetor)
m
$\Phi$
Phi
Fluxo magnético
kg/C s
$\vec{F}$
&F
Força
N
$\mu_r$
mu_r
Permeabilidade magnética relativa
-
$r$
r
Rádio
m
$S$
S
Seção por onde passam as linhas de campo
m^2
$t$
t
Tempo
s
$\Delta t$
Dt
Variação de tempo
s
$\Delta\Phi$
DPhi
Variação do fluxo magnético
kg/C s
$v$
v
Velocidade do condutor
m/s
$\hat{r}$
&n
Versor radial (inversor)
-
Cálculos
Primeiro, selecione a equação: 
para 
,
depois, selecione a variável: 
para 
para ,
depois, selecione a variável:
para
Símbolo
Equação
Resolvido
Traduzido
Cálculos
Símbolo
Equação
Resolvido
Traduzido
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Exemplos
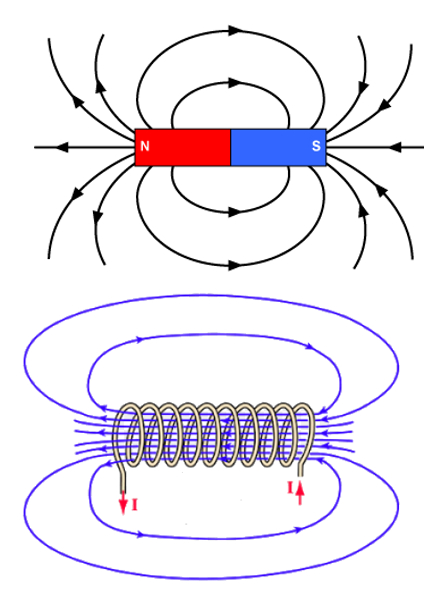
Wenn Strom durch einen Solenoiden flie en darf, beobachten wir, dass ein Magnetfeld erzeugt wird, das dem eines magnetisierten Stabes hnelt. Dies bedeutet, dass der Elektronenstrom in der Lage ist, Magnetfelder zu erzeugen, die denen von permanenten Magneten quivalent sind.
(ID 12116)
(ID 12121)
(ID 12174)
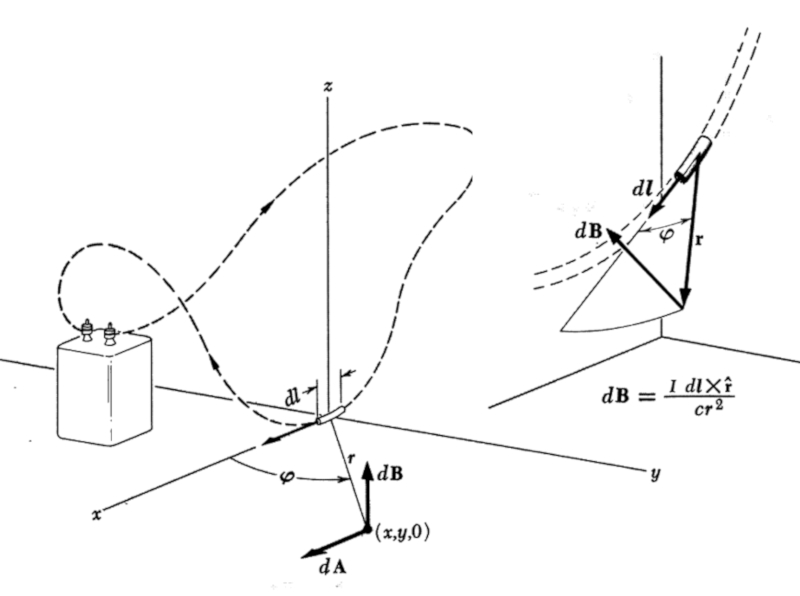
Um campo magn tico constru do com base nas contribui es coletivas de todos os elementos que conduzem eletricidade. Quando focamos em um desses elementos em particular, podemos observar como ele participa no campo magn tico, conforme ilustrado na imagem:
(ID 12179)
ID:(1626, 0)