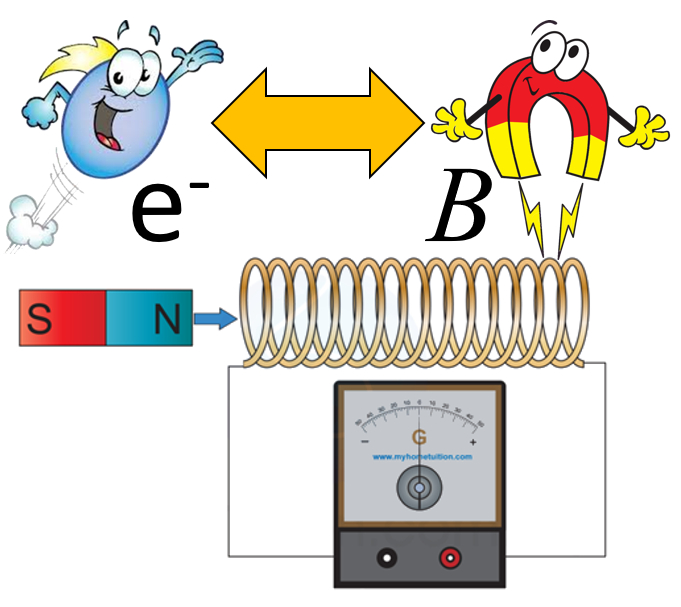
Faradaysches Gesetz und Magnetfeld
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
None
(ID 12171)
Beispiele
SI se deja circular corriente por un solenoide se observa que se cera un campo magn tico similar al de una barra imantada. Esto significa que la corriente de electrones es capaz de generar campos magn ticos y que estos son equivalentes a aquellos campos magn ticos permanentes.
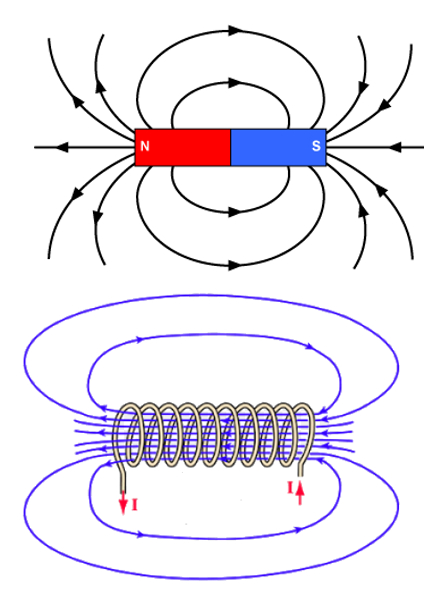
(ID 12116)

(ID 1932)
Al igual que en la mec nica en que la inercia trata de resistirse al cambio de estado en la electrodin mica existe un fen meno an logo que fue descrito inicialmente por Lenz. Este se observa en particular en la inducci n magn tica en que las corrientes generadas son siempre de modo de oponerse al im n que las esta generando. En otras palabras las corrientes generadas crean un campo magn tico que esta en oposici n al que las origina inicialmente. Esto es lo que se denomina la ley de Lenz.
Ejemplo de la aplicaci n de la ley de Lenz: si se deja caer un anillo sobre un campo magn tico se genera en el una corriente tal que genera un campo de polaridad opuesta que se resiste a caer sobre el campo existente.
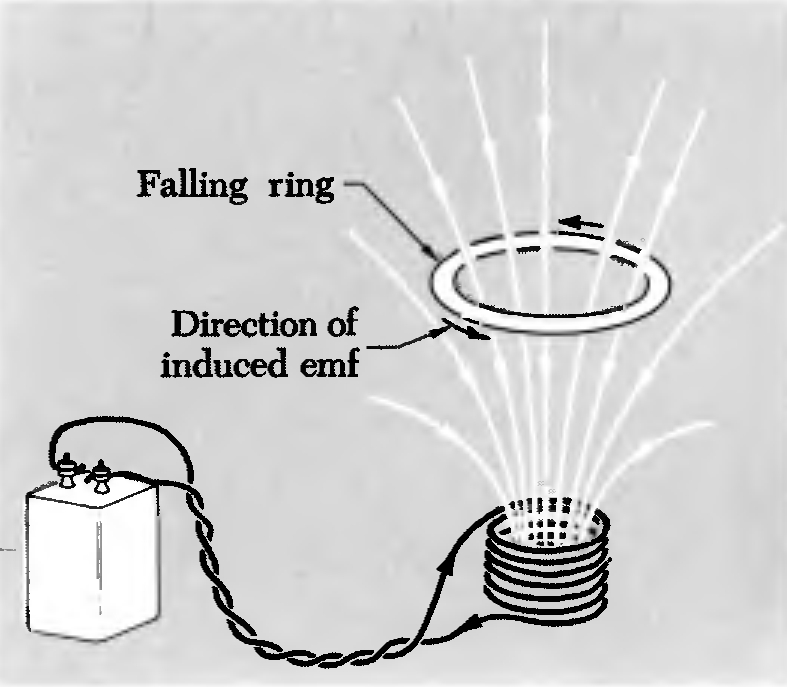
(ID 12174)
Ein Magnetfeld entsteht durch die Kombination der Beitr ge aller Elemente, die elektrischen Strom leiten. Wenn wir uns auf eines dieser speziellen Elemente konzentrieren, k nnen wir beobachten, wie es zur Bildung des Magnetfelds beitr gt, wie in der Abbildung dargestellt:
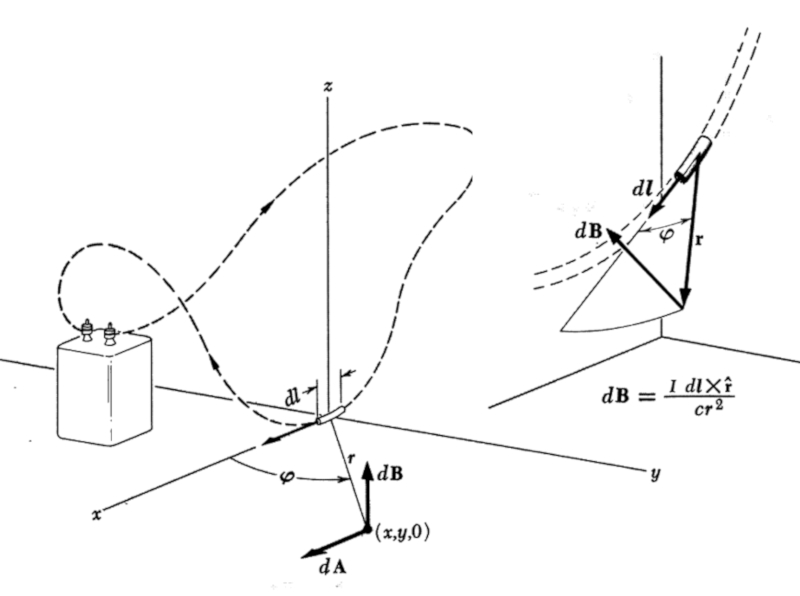
(ID 12179)
ID:(1626, 0)