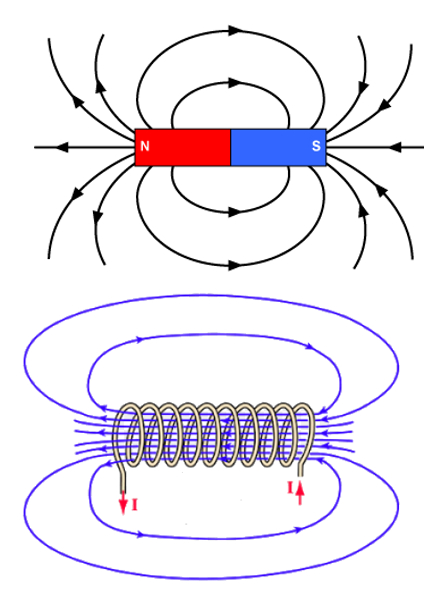
Cuando se permite que circule corriente a trav s de un solenoide, observamos que se crea un campo magn tico similar al de una barra imantada. Esto significa que la corriente de electrones es capaz de generar campos magn ticos y que estos son equivalentes a los campos magn ticos permanentes.

(ID 12116)

(ID 1932)

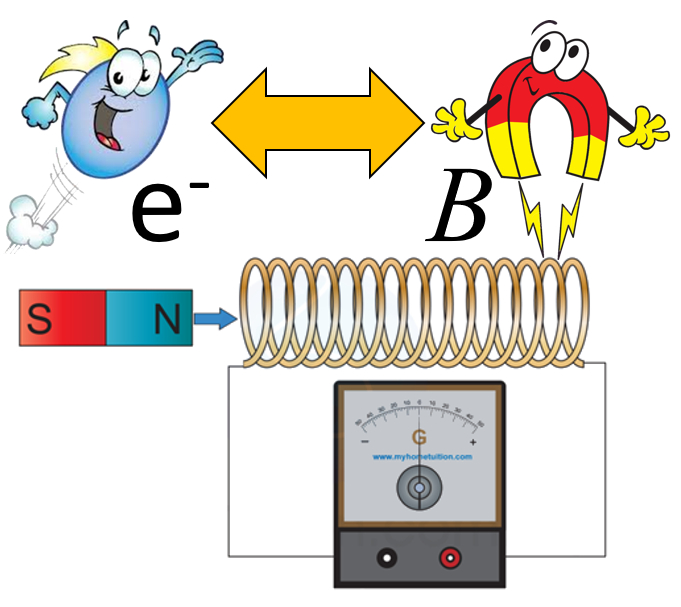
No solo existe una similitud entre el campo magn tico de un im n y aquel que genera un solenoide, tambi n interactuan en forma similar a como lo hacen dos imanes.

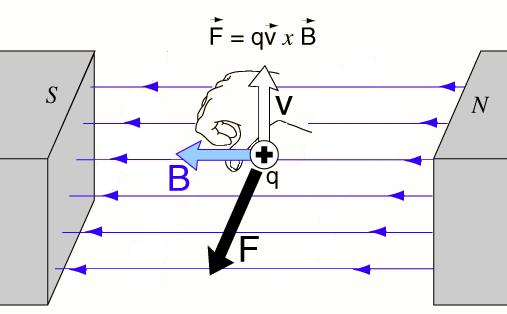
Sin embargo existe una diferencia clave, el im n interactua con el spin del electr n y altera su comportamiento. O sea

- el campo magn tico puede inducir un comportamiento en el electr n (principio del generador el ctrico)

- el electr n puede generar un campo magn tico y v a este mover un im n o el objeto que lo crea (principio del motor el ctrico)

(ID 12121)

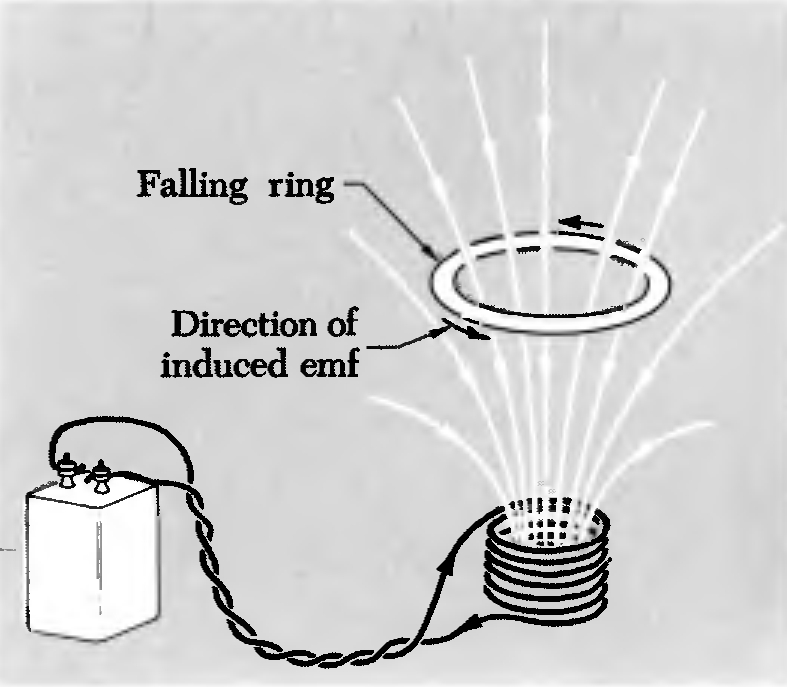
Al igual que en la mec nica en que la inercia trata de resistirse al cambio de estado en la electrodin mica existe un fen meno an logo que fue descrito inicialmente por Lenz. Este se observa en particular en la inducci n magn tica en que las corrientes generadas son siempre de modo de oponerse al im n que las esta generando. En otras palabras las corrientes generadas crean un campo magn tico que esta en oposici n al que las origina inicialmente. Esto es lo que se denomina la ley de Lenz.

Ejemplo de la aplicaci n de la ley de Lenz: si se deja caer un anillo sobre un campo magn tico se genera en el una corriente tal que genera un campo de polaridad opuesta que se resiste a caer sobre el campo existente.

(ID 12174)

Un campo magn tico se genera mediante la combinaci n de m ltiples contribuciones de todos los elementos que conducen electricidad. Si nos enfocamos en uno de estos elementos en particular, podemos observar su contribuci n al campo magn tico, como se ilustra en la imagen:

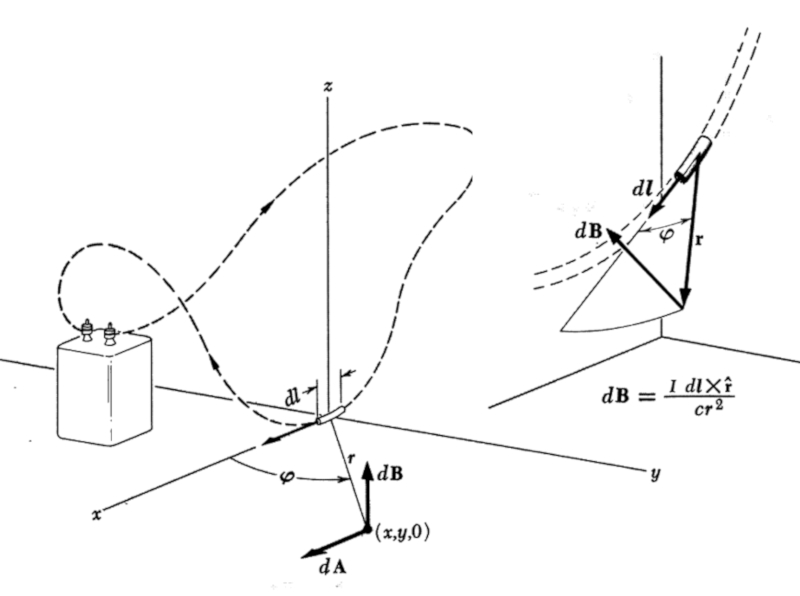
(ID 12179)