Druyd:Knowledge

Loi de Faraday et champ magnétique

Storyboard

>Modèle

ID:(1626, 0)

Ferromagnétique ou solénoïde

Définition

ID:(12116, 0)

Interaction aimant et solénoïde

Image

ID:(12121, 0)

La loi de Lenz

Noter

ID:(12174, 0)

Calcul d'un champ magnétique

Citation

ID:(12179, 0)

Loi de Faraday et champ magnétique

Description

Variables

Symbole

Texte

Variable

Valeur

Unités

Calculer

Valor MKS

Unités MKS

$\vec{H}$

Champ magnétique, vecteur

V/m

$q$

Charge d'essai

$\mu_0$

mu_0

Constante de champ magnétique

kg m/C^2

$I$

Courant

$B$

Densité de flux magnétique

$\vec{B}$

Densité de flux magnétique (vecteur)

$\Delta\varphi$

Dphi

Différence potentielle

$d\vec{H}$

d&H

Élément de champ magnétique (vecteur)

V/m

$d\vec{s}$

d&s

Élément de longueur (vecteur)

$\Phi$

Phi

Flux magnétique

kg/C s

$\vec{F}$

Force

$L$

Longueur du pilote

$\mu_r$

mu_r

Perméabilité magnétique relative

$r$

Radio

$S$

Section par laquelle passent les lignes de champ

m^2

$t$

Temps

$\Delta\Phi$

DPhi

Variation du flux magnétique

kg/C s

$\Delta t$

Variation temporelle

$\hat{r}$

Vertisseur radial (verter)

$v$

Vitesse du conducteur

m/s

Calculs

Équation

Nombre

D'abord, sélectionnez l'équation:

, puis, sélectionnez la variable:

Symbole

Équation

Résolu

Traduit

Calculs

Symbole

Équation

Résolu

Traduit

Variable

Donnée

Calculer

Cible :

Équation

À utiliser

Équations

$ \vec{F} = q \vec{v} \times \vec{B} $

&F = q * &v # &B

(ID 10056)

$ \Phi =\displaystyle\int_S\vec{B}\cdot d\vec{S} $

Phi = @INT( &B , S )

(ID 12168)

$ \vec{B} = \mu_0 \mu_r \vec{H}$

&B = mu_0 * mu_r * &H

(ID 12171)

$ \Delta\varphi = -\displaystyle\frac{d \Phi }{d t }$

Dvarphi = dPhi / dt

(ID 12175)

$ \Delta\varphi = - B L v$

Dvarphi = - B * L * v

(ID 12177)

$ d\vec{H}= \displaystyle\frac{ I }{4\pi}\displaystyle\frac{ d\vec{l}\times \hat{r}}{r^2}$

d&H = I * d&l # &r /(4* pi * r^2)

(ID 12178)

$ \Delta\varphi = -\displaystyle\frac{ \Delta\Phi }{ \Delta t }$

Dvarphi = DPhi / Dt

(ID 12256)

Exemples

Ferromagn tique ou sol no de

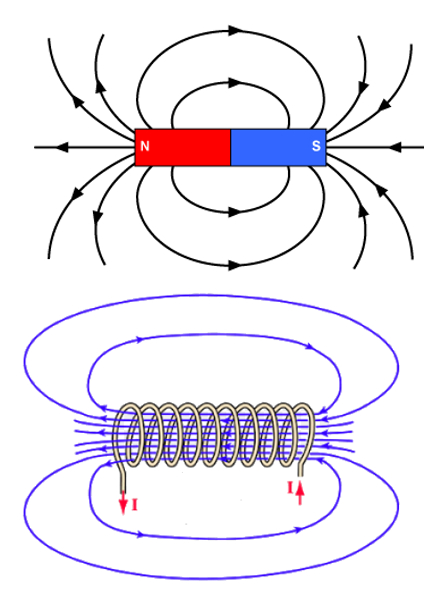
Lorsque un courant est autoris circuler travers un sol no de, nous observons qu'il cr e un champ magn tique similaire celui d'une barre aimant e. Cela signifie que le courant d' lectrons est capable de g n rer des champs magn tiques, et que ces champs sont quivalents aux champs magn tiques permanents.

(ID 12116)

Interaction aimant et sol no de

(ID 12121)

La loi de Lenz

(ID 12174)

Calcul d'un champ magn tique

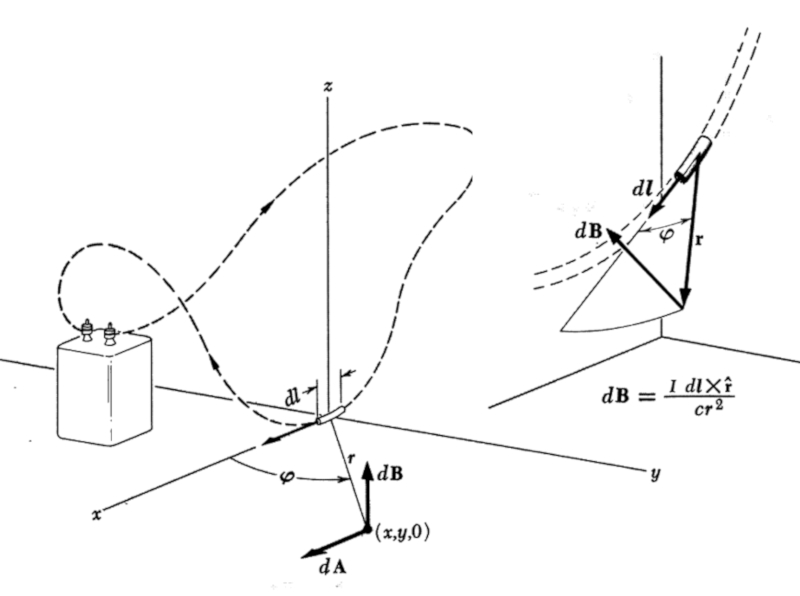
Un champ magn tique est construit en fonction des contributions collectives de tous les l ments conducteurs d' lectricit . Lorsque nous examinons l'un de ces l ments en particulier, nous pouvons observer comment il participe au champ magn tique, comme illustr dans l'image :

(ID 12179)

ID:(1626, 0)