User:
Gauss's theorem
Storyboard 
Gauss's law says that if you have a closed surface and add the projection of the electric field over the entire surface is proportional to the charge contained in the volume.
ID:(824, 0)
Flux of a charge
Image
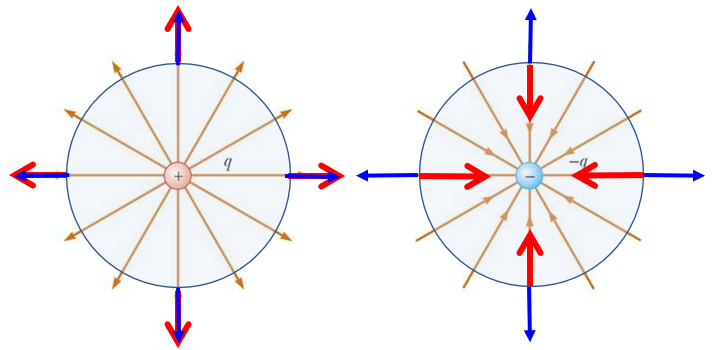
If the surface surrounds a load it is observed that there is no compensation and that the flow only depends on the sign of the load:
• if the charge is positive, the normal versers are parallel to the field and the flow is positive
• if the charge is negative the normal versors are anti parallel to the field and the flow is negative
ID:(1776, 0)
Flow of two opposite charges
Image
If two opposite charges are considered and the flow through a surface containing both is studied, we observe that the flows are compensated again, being in the end the total flow null. In this way we conclude that:
• there is no full flow in a volume that does not contain charges
• there is no total flow in a volume that contains an equal number of positive and negative charges
• there is only total flow to the extent that there are loads whose total sum is not zero
ID:(11375, 0)
Flow through a closed volume without loads
Image
If a volume element is taken and placed in an electric flow, it will be observed that one side of the body is oriented along the field while the opposite side is oriented in the opposite direction to the field:
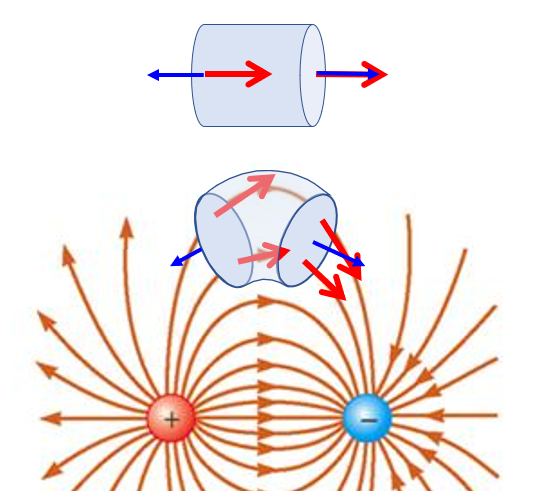
This leads to the flow that 'goes out' being compensated for the flow that 'goes in'. This is only if there are no charges inside, that is, there is no source or sink that generates or destroys field lines. In this sense, one can speak of the conservation of the flow as in a liquid.
ID:(1777, 0)
Gauss's law
Concept
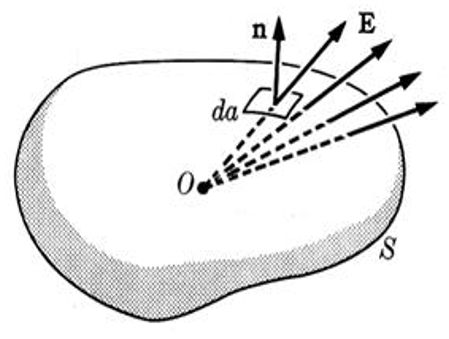
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element
i, which is then summed over the entire section:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
The magnitude of the electric eield ($E$) generated by the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$) as follows:
| $ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$ |
Given that the surface of a sphere ($S$) is with the distance ($r$):
| $ S = 4 \pi r ^2$ |
The flux is:
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
From this, we can infer that the relationship is:
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Using the surface element ($dS$) for the dot product of the electric field ($\vec{E}$) and the versor normal to the section ($\hat{n}$), we obtain the continuous version of Gauss's law:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
This corresponds to the version of Gauss's equation discovered in 1835, which was published posthumously [1].
[1] "Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskräfte" (General Propositions Relating to the Forces of Attraction and Repulsion which Act in Proportion to the Inverse Square of the Distance), Carl Friedrich Gauss, Werke, 1867
ID:(15791, 0)
Graphic representation of Gauss's law
Image
Gauss's law considers the field lines with respect to a closed surface.
• If the surface does not enclose any charge, the field lines are conserved, meaning they flow both into and out of the surface.
• If the surface encloses a charge the total charge ($Q_t$), a number proportional to that charge is either created (positive charge) or destroyed (negative charge).
• If the sum of the enclosed charges is zero, the sum of the components of the field perpendicular to the surface will also be zero.
ID:(224, 0)
Application to the case of a field inside a conductor
Image
Inside a conductor you can define a surface
therefore the electric field is null. The driver generates what is called a Faraday cage.
ID:(1924, 0)
Example of null field inside a conductor
Image
The fuselage of a passenger airplane is generally a good conductor of electricity. Therefore, if an airplane is struck by lightning, the charges distribute over its surface and, according to Gauss's law, no electric field is generated inside the aircraft.
| $ E =0$ |
As a result, passengers are not harmed, and eventually, the charge continues its path, creating a new lightning strike that moves to another positively charged location.
This is why lightning strikes are considered not dangerous for aircraft in flight, and each airplane experiences several strikes per year. However, there is a risk during landing; if the airplane is struck by lightning as it touches down, the charges can flow through the tires to the runway, generating heat levels that can damage them. Pilots are generally trained to handle situations where the landing gear is damaged, so the risk to passengers is not very high. However, the damage to the aircraft can be significant and may require extensive repairs before it can return to service.
ID:(11374, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
@SUM( &E_i * &n_i * dS_i , i , 1 , N ) = Q /( epsilon * epsilon_0 )
$ E =0$
E =0
$ Q = \displaystyle\sum_ i ^ N q_i$
Q =@SUM( q_i , i , 1 , N )
$\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$
int_S E n dS=Q/(e_0 e)
ID:(15783, 0)
Sum of all charges
Equation
The flux depends on the total charge ($Q_t$) contained within the volume. Therefore, we must sum all the charge i ($q_i$) contained, regardless of their position:
| $ Q = \displaystyle\sum_ i ^ N q_i$ |
ID:(11376, 0)
Discrete Gauss's law
Equation
The surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element $i$, and then summed over the entire section, are equal to the total charge ($Q_t$) divided by the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$):
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element
i, which is then summed over the entire section:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
The magnitude of the electric eield ($E$) generated by the charge ($Q$), which are at a distance of the distance ($r$), is calculated using the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$) as follows:
| $ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$ |
Given that the surface of a sphere ($S$) is with the distance ($r$):
| $ S = 4 \pi r ^2$ |
The flux is:
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
From this, we can infer that the relationship is:
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
ID:(11377, 0)
Gauss' law in integral version
Equation
Using the surface element ($dS$) for the dot product of the electric field ($\vec{E}$) and the versor normal to the section ($\hat{n}$), and the total charge ($Q_t$) divided by the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$), we arrive at the expression for Gauss's law:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
The surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element $i$, which is then summed over the entire section, is equal to the total charge ($Q_t$) divided by the electric field constant ($\epsilon_0$) and the dielectric constant ($\epsilon$):
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Using the surface element ($dS$) for the dot product of the electric field ($\vec{E}$) and the versor normal to the section ($\hat{n}$), we obtain the continuous version of Gauss's law:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
ID:(3213, 0)
Field in the interior of a Conductor
Equation
Consider a hollow charge, i.e., a hollow sphere with charges on its surface. In this case, we can define an internal surface within the sphere. Since the amount of charge the total charge ($Q_t$) contained within the volume is zero, the electric field the electric eield ($E$) will also be zero:
| $ E =0$ |
None
ID:(3842, 0)