Utilisateur:
Loi de Gauss
Concept 
Le flux électrique ($\Phi$) est définie comme la composante normale du champ électrique, calculée à partir de le champ électrique sur la surface i ($\vec{E}_i$) et le versor normal à la surface i ($\hat{n}_i$), multipliée par a élément de surface i ($dS_i$) pour chaque élément
i, puis sommée sur toute la section :
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
La magnitude de le champ électrique ($E$) générée par a charge ($Q$), qui se trouvent à une distance de a distance ($r$), est calculée en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) de la manière suivante :
| $ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$ |
Étant donné que a surface d'une sphère ($S$) est avec a distance ($r$) :
| $ S = 4 \pi r ^2$ |
Le flux est :
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
À partir de cela, nous pouvons en déduire que la relation est :
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
En utilisant le élément surfacique ($dS$) pour le produit scalaire de le champ électrique ($\vec{E}$) et le versor normal à la section ($\hat{n}$), nous obtenons la version continue de la loi de Gauss :
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Ceci correspond à la version de l'équation de Gauss découverte en 1835, qui a été publiée à titre posthume [1].
[1] 'Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskräfte' (Propositions générales relatives aux forces d'attraction et de répulsion qui agissent en proportion inverse du carré de la distance), Carl Friedrich Gauss, Werke, 1867
ID:(15791, 0)
Représentation graphique de la loi de Gauss
Image
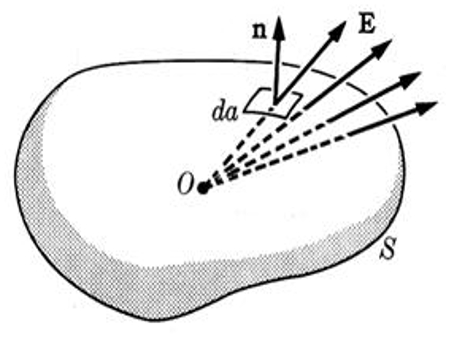
La loi de Gauss considère les lignes de champ par rapport à une surface fermée.
• Si la surface n'enferme aucune charge, les lignes de champ sont conservées, c'est-à-dire qu'elles circulent autant vers l'intérieur que vers l'extérieur de la surface.
• Si la surface entoure une charge a charge totale ($Q_t$), un nombre proportionnel à cette charge est créé (charge positive) ou détruit (charge négative).
• Si la somme des charges contenues est nulle, la somme des composantes du champ perpendiculaires à la surface sera également nulle.
ID:(224, 0)
Exemple de champ nul à l'intérieur d'un conducteur
Image
Le fuselage d'un avion de passagers est généralement un bon conducteur d'électricité. Par conséquent, si un avion est frappé par la foudre, les charges se répartissent sur sa surface et, selon la loi de Gauss, aucun champ électrique n'est généré à l'intérieur de l'avion.
| $ E =0$ |
Ainsi, les passagers ne subissent aucun dommage et finalement, la charge continue son chemin, créant un nouvel éclair qui se déplace vers un autre endroit chargé positivement.
C'est pourquoi on considère que les éclairs ne sont pas dangereux pour les avions en vol et que chaque avion est frappé plusieurs fois par an. Cependant, il existe un risque pendant le processus d'atterrissage : si l'avion est touché par la foudre au moment où il touche le sol, les charges peuvent traverser les pneus jusqu'à la piste, générant des niveaux de chaleur qui peuvent les endommager. En général, les pilotes sont formés pour gérer des situations où le train d'atterrissage est endommagé, de sorte que le risque pour les passagers n'est pas très élevé. Cependant, les dommages à l'avion peuvent être importants et nécessiter des réparations plus étendues avant qu'il puisse reprendre son service.
ID:(11374, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
@SUM( &E_i * &n_i * dS_i , i , 1 , N ) = Q /( epsilon * epsilon_0 )
$ E =0$
E =0
$ Q = \displaystyle\sum_ i ^ N q_i$
Q =@SUM( q_i , i , 1 , N )
$\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$
int_S E n dS=Q/(e_0 e)
ID:(15783, 0)
Somme de toutes les charges
Équation
Le flux dépend de a charge totale ($Q_t$) contenu dans le volume. Par conséquent, nous devons additionner tous les a charge i ($q_i$) contenus, indépendamment de leur position :
| $ Q = \displaystyle\sum_ i ^ N q_i$ |
ID:(11376, 0)
Loi de Gauss discrète
Équation
Le champ électrique sur la surface i ($\vec{E}_i$) et le versor normal à la surface i ($\hat{n}_i$), multipliés par a élément de surface i ($dS_i$) pour chaque élément $i$, puis additionnés sur toute la section, sont égaux à A charge totale ($Q_t$) divisé par a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) :
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Le flux électrique ($\Phi$) est définie comme la composante normale du champ électrique, calculée à partir de le champ électrique sur la surface i ($\vec{E}_i$) et le versor normal à la surface i ($\hat{n}_i$), multipliée par a élément de surface i ($dS_i$) pour chaque élément
i, puis sommée sur toute la section :
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
La magnitude de le champ électrique ($E$) générée par a charge ($Q$), qui se trouvent à une distance de a distance ($r$), est calculée en utilisant a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) de la manière suivante :
| $ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$ |
Étant donné que a surface d'une sphère ($S$) est avec a distance ($r$) :
| $ S = 4 \pi r ^2$ |
Le flux est :
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
À partir de cela, nous pouvons en déduire que la relation est :
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
ID:(11377, 0)
Loi de Gauss discrète
Équation
En utilisant le élément surfacique ($dS$) pour le produit scalaire de le champ électrique ($\vec{E}$) et le versor normal à la section ($\hat{n}$), et a charge totale ($Q_t$) divisé par a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$), nous arrivons à l'expression de la loi de Gauss :
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Le champ électrique sur la surface i ($\vec{E}_i$) et le versor normal à la surface i ($\hat{n}_i$), multipliés par a élément de surface i ($dS_i$) pour chaque élément $i$, puis additionnés sur toute la section, sont égaux à A charge totale ($Q_t$) divisé par a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$) :
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
En utilisant le élément surfacique ($dS$) pour le produit scalaire de le champ électrique ($\vec{E}$) et le versor normal à la section ($\hat{n}$), nous obtenons la version continue de la loi de Gauss :
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
ID:(3213, 0)
Champ à l'intérieur d'un conducteur
Équation
Considérons une charge creuse, c'est-à-dire une sphère creuse avec des charges sur sa surface. Dans ce cas, nous pouvons définir une surface interne à l'intérieur de la sphère. Puisque la quantité de charge a charge totale ($Q_t$) contenue dans le volume est nulle, le champ électrique le champ électrique ($E$) sera également nul :
| $ E =0$ |
ID:(3842, 0)