User:
Electric flow concept
Image 
Flow is defined by the electric field and the section that the field lines traverse:
ID:(11366, 0)
Electric field projection
Concept
The dot product of two vectors $\vec{a}$ and $\vec{b}$ can be calculated using the magnitudes of the vectors and the angle $\theta$ between them, as follows:
| $ \vec{a}\cdot\vec{b} = \mid\vec{a}\mid \mid\vec{b}\mid \cos \theta $ |
Since the versor normal to the section ($\hat{n}$) has a magnitude of one, the electric field projection ($E_n$) with the electric field ($\vec{E}$), the versor normal to the section ($\hat{n}$), and the surface normal electric field angle ($\alpha$) is:
| $ \vec{E} \cdot \hat{n} =\mid \vec{E} \mid\cos \alpha $ |
ID:(15789, 0)
Electric flow geometry
Concept
The field is not necessarily orthogonal to the section through which the flux is being calculated. Therefore, it is necessary to calculate the component of the electric field that is orthogonal to the section:
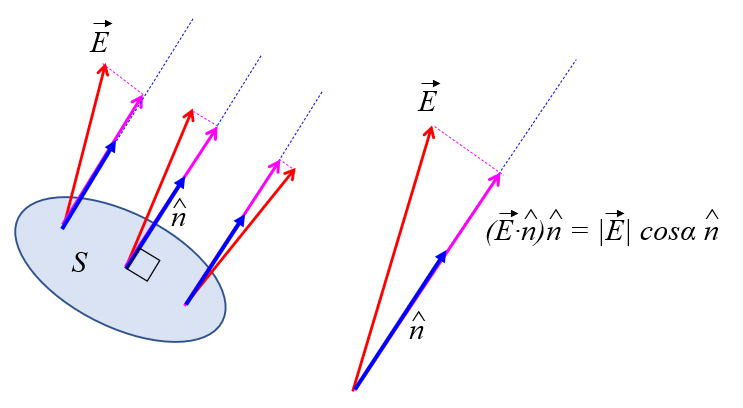
Since the dot product of a vector with a unit vector, in this case, the unit vector that defines the orientation of the section, gives the projection of the vector onto this section, the component to consider is the dot product or the cosine of the angle the surface normal electric field angle ($\alpha$) between the electric field ($\vec{E}$) and the versor normal to the section ($\hat{n}$):
| $ \vec{E} \cdot \hat{n} =\mid \vec{E} \mid\cos \alpha $ |
ID:(11368, 0)
Flow by non-flat section and variable field
Concept
As the section is not necessarily flat, the normal versor may vary its orientation. Similarly, the field can vary in direction and magnitude on the section. Therefore, the section can be segmented into small surface elements that can be considered flat at first approximation and in which the field does not vary either in direction or in magnitude:
Therefore, the electric flow ($\Phi$) is calculated by summing, over the entire section, the contribution of the normal component of the electric field to each element of the section, calculated from the surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), and multiplied by the surface element i ($dS_i$):
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
In the continuous limit, the sum can be replaced by the integral over the surface element ($dS$) of the dot product of the electric field ($\vec{E}$) and the versor normal to the section ($\hat{n}$):
| $ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $ |
ID:(11373, 0)
The electric flow, depending on the angle
Concept
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element $i$, which is then summed over the entire section:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
On the other hand, the electric field projection ($E_n$) with the electric field ($\vec{E}$), the versor normal to the section ($\hat{n}$), and the surface normal electric field angle ($\alpha$) is equal to:
| $ \vec{E} \cdot \hat{n} =\mid \vec{E} \mid\cos \alpha $ |
Therefore, with the surface normal electric field angle i ($\alpha_i$) we have:
| $ \Phi = \displaystyle\sum_i | \vec{E}_i | \cos\alpha_i dS $ |
This can be extended to the continuous case by replacing the sum with an integral over the surface element ($dS$) of the dot product of the electric field ($\vec{E}$) and the surface normal electric field angle ($\alpha$):
| $ \Phi = \displaystyle\int | \vec{E} | \cos \alpha dS $ |
ID:(15790, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \vec{E} \cdot \hat{n} =\mid \vec{E} \mid\cos \alpha $
&E * &n = @MOD( &E )*cos( alpha )
$ \Phi = \displaystyle\sum_i | \vec{E}_i | \cos\alpha_i dS $
Phi = dS_i *@MAG( &E_i )* cos( alpha_i )
$ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $
Phi = S * &n * &E
$ \Phi = \displaystyle\int | \vec{E} | \cos \alpha dS $
Phi = S * @MAG( &E ) * cos( alpha )
$ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $
Phi = sum(S_i * n_i * E_i,i)
ID:(15788, 0)
Electric field projection
Equation
The electric field projection ($E_n$) is with the electric field ($\vec{E}$), the versor normal to the section ($\hat{n}$) and the surface normal electric field angle ($\alpha$) equal to:
| $ \vec{E} \cdot \hat{n} =\mid \vec{E} \mid\cos \alpha $ |
The dot product of two vectors $\vec{a}$ and $\vec{b}$ can be calculated using the magnitudes of the vectors and the angle $\theta$ between them, as follows:
| $ \vec{a}\cdot\vec{b} = \mid\vec{a}\mid \mid\vec{b}\mid \cos \theta $ |
Since the versor normal to the section ($\hat{n}$) has a magnitude of one, the electric field projection ($E_n$) with the electric field ($\vec{E}$), the versor normal to the section ($\hat{n}$), and the surface normal electric field angle ($\alpha$) is:
| $ \vec{E} \cdot \hat{n} =\mid \vec{E} \mid\cos \alpha $ |
ID:(11371, 0)
The electrical flow
Equation
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element $i$, which is then summed over the entire section:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
ID:(11372, 0)
The general electrical flow
Equation
The electric flow ($\Phi$) is equal to the integral over the surface element ($dS$) of the dot product of the electric field ($\vec{E}$) and the versor normal to the section ($\hat{n}$):
| $ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $ |
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element $i$, which is then summed over the entire section:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
In the continuous limit, the sum can be replaced by the integral over the surface element ($dS$) of the dot product of the electric field ($\vec{E}$) and the versor normal to the section ($\hat{n}$):
| $ \Phi = \displaystyle\int \vec{E} \cdot \hat{n} dS $ |
ID:(11367, 0)
The electric flow, depending on the angle
Equation
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the surface normal electric field angle i ($\alpha_i$), multiplied by the surface element i ($dS_i$) for each element $i$, which is then summed over the entire section:
| $ \Phi = \displaystyle\sum_i | \vec{E}_i | \cos\alpha_i dS $ |
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the versor normal to surface i ($\hat{n}_i$), multiplied by the surface element i ($dS_i$) for each element $i$, which is then summed over the entire section:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
On the other hand, the electric field projection ($E_n$) with the electric field ($\vec{E}$), the versor normal to the section ($\hat{n}$), and the surface normal electric field angle ($\alpha$) is equal to:
| $ \vec{E} \cdot \hat{n} =\mid \vec{E} \mid\cos \alpha $ |
Therefore, with the surface normal electric field angle i ($\alpha_i$) we have:
| $ \Phi = \displaystyle\sum_i | \vec{E}_i | \cos\alpha_i dS $ |
ID:(11370, 0)
The general electrical flow, as a function of the angle
Equation
The electric flow ($\Phi$) is equal to the integral over the surface element ($dS$) of the dot product of the electric field ($\vec{E}$) and the surface normal electric field angle ($\alpha$):
| $ \Phi = \displaystyle\int | \vec{E} | \cos \alpha dS $ |
The electric flow ($\Phi$) is defined as the normal component of the electric field, calculated from the surface electric field i ($\vec{E}_i$) and the surface normal electric field angle i ($\alpha_i$), multiplied by the surface element i ($dS_i$) for each element $i$, which is then summed over the entire section:
| $ \Phi = \displaystyle\sum_i | \vec{E}_i | \cos\alpha_i dS $ |
This can be extended to the continuous case by replacing the sum with an integral over the surface element ($dS$) of the dot product of the electric field ($\vec{E}$) and the surface normal electric field angle ($\alpha$):
| $ \Phi = \displaystyle\int | \vec{E} | \cos \alpha dS $ |
ID:(11369, 0)