Druyd:Knowledge

Ley de Ohm

Storyboard

Si se aplica un campo a una carga se obtiene una fuerza. Dicha fuerza aplicada a lo largo de un camino lleva a una energía potencial. Si se expresa con un campo eléctrico se obtiene la energía potencial por carga que denominamos potencial eléctrico. El potencial eléctrico genera desplazamiento de cargas lo que implica que existe un flujo que denominamos corriente eléctrica. Su magnitud depende del potencial eléctrico y de la resistencia que presenta el material en que están los electrones que denominaremos conductor. La ley resultante es la llamada ley de Ohm.

>Modelo

ID:(815, 0)

Corriente por un conductor

Definición

ID:(7860, 0)

Resistencia y calor

Imagen

ID:(11761, 0)

Ley de Ohm

Descripción

Cuando se aplica un campo a una carga, se genera una fuerza. Esta fuerza, al actuar a lo largo de un camino, da lugar a una energía potencial. Si esta energía potencial se expresa en términos de un campo eléctrico, obtenemos la energía potencial por unidad de carga, conocida como potencial eléctrico. El potencial eléctrico induce el desplazamiento de cargas, generando un flujo denominado corriente eléctrica. La magnitud de esta corriente depende tanto del potencial eléctrico aplicado como de la resistencia que presenta el material a través del cual se desplazan las cargas, comúnmente conocido como conductor. La relación resultante entre el potencial eléctrico, la corriente y la resistencia está descrita por la conocida ley de Ohm.

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$a$

Aceleración de cargas en conductor

m/s^2

$E$

Campo eléctrico

V/m

$c$

Concentración de cargas

1/m^3

$I$

Corriente

$\Delta\varphi$

Dphi

Diferencia de potencial

$\Delta Q$

Elemento de carga

$L$

Largo del conductor

$R$

Resistencia

Ohm

$\rho_e$

rho_e

Resistividad

Ohm m

$S$

Sección del Conductor

m^2

$\tau$

tau

Tiempo entre choques

$\Delta t$

Tiempo transcurrido

$v_{max}$

v_max

Velocidad máxima

m/s

$\bar{v}$

v_m

Velocidad media de las cargas

m/s

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$ \Delta\varphi = R I $

Dphi = R * I

None

(ID 3214)

$ v_{max} =\displaystyle\frac{ e E }{ m_e } \tau $

v_max =( e * E/ m_e )* tau

(ID 3836)

$ I =\displaystyle\frac{ e ^2 E }{2 m_e } \tau c S $

I = e ^2* E * tau * c * S /(2* m_e )

(ID 3837)

$ E =\displaystyle\frac{ \Delta\varphi }{ L }$

E = Dphi / L

(ID 3838)

$ \Delta\varphi =\displaystyle\frac{2 m_e }{ e ^2 \tau c }\displaystyle\frac{ L }{ S } I $

Dphi =(2 * m_e /( e ^2* tau * c ))*( L / S )* I

(ID 3839)

$ \rho_e =\displaystyle\frac{2 m_e }{ e ^2 \tau c }$

rho_e =2* m_e /( e ^2* tau * c )

(ID 3840)

$ R = \rho_e \displaystyle\frac{ L }{ S }$

R = rho_e * L / S

(ID 3841)

$ a =\displaystyle\frac{ e E }{ m_e }$

a = e * E / m_e

(ID 3843)

$ I = e S c \bar{v} $

I = e * S * c * v_m

(ID 10400)

$ I =\displaystyle\frac{ \Delta Q }{ \Delta t }$

I = DQ / Dt

(ID 10401)

$ v_{max} = a \tau $

v_max = a * tau

(ID 16236)

$ \overline{v} =\displaystyle\frac{1}{2} v_{max} $

v_m = v_max / 2

(ID 16237)

Ejemplos

Simulación del modelo de resistencia

(ID 16003)

Corriente por un conductor

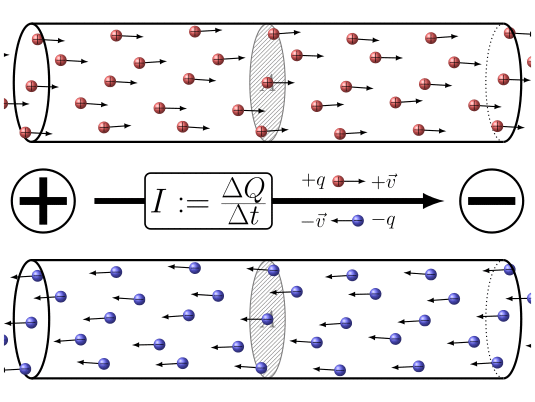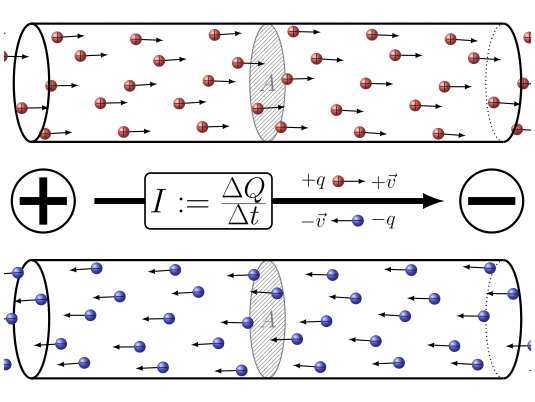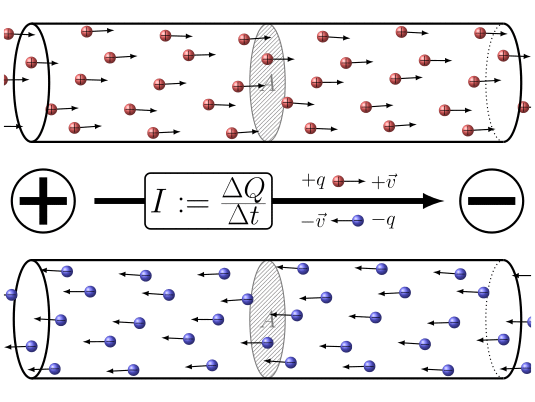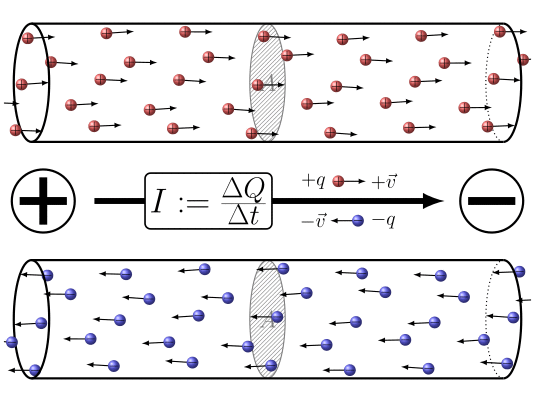
En resumen la aplicaci n de una diferencia de potencial entre los dos extremos del conductor \Delta\varphi genera una corriente I que depende de la resistencia R:

(ID 7860)

Resistencia y calor

El calor hace que los tomos oscila con una mayor amplitud dificultando el avance de los electrones:

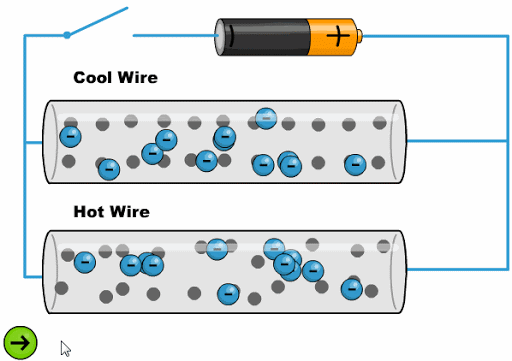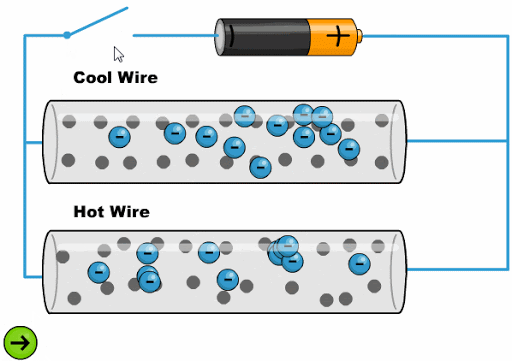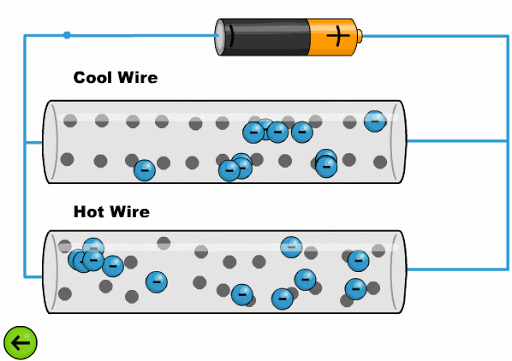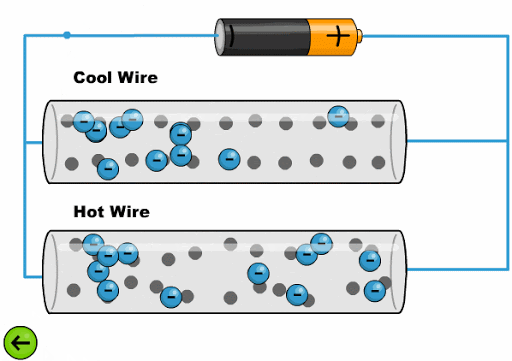
(ID 11761)

Modelo

(ID 16002)

ID:(815, 0)