Cuando estudiamos un circuito podemos determinar en forma directa las respectivas resistencias y potenciales de las fuentes (ej. baterias). Todos estos par metros determinan como la corriente fluir por el sistema. Esto se puede medir, si existe el circuito, o calcular, cuando se esta dise ado y aun no se cuenta con el sistema f sicamente.

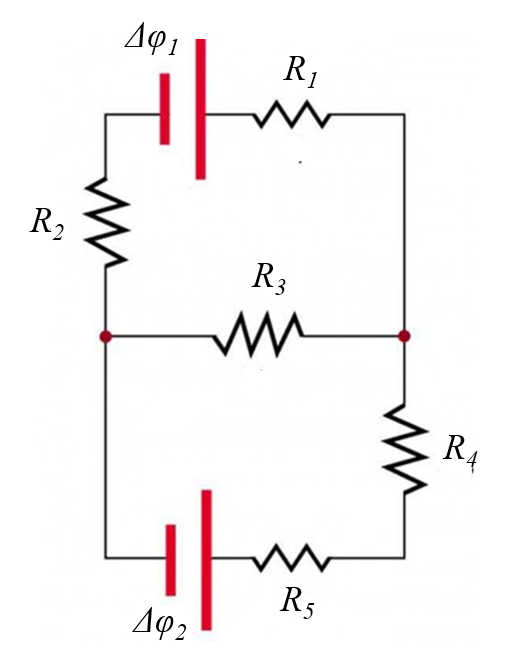
La pregunta es como se pueden calcular dichas corrientes.

(ID 12060)

Para determinar las corrientes debemos primero definir aquellas que pueden existir.

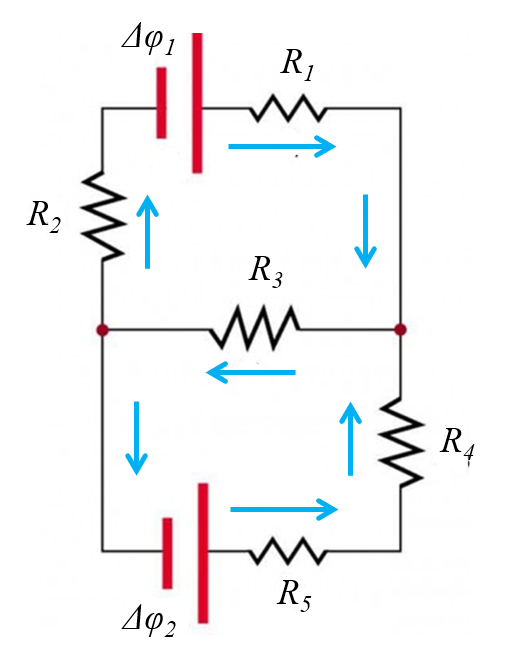
Para ello se debe comprender que las cargas se conservan, por lo que la corriente:

No varia a lo largo de una secuencia de elementos que no tienen otro conector

En cada bifurcaci n la suma total de flujos debe ser nula (o sea entran tantos electrones como salen)

(ID 12061)

En cada nodo las corrientes que arriban deben en suma ser iguales a la suma de las que salen. En el caso de la imagen

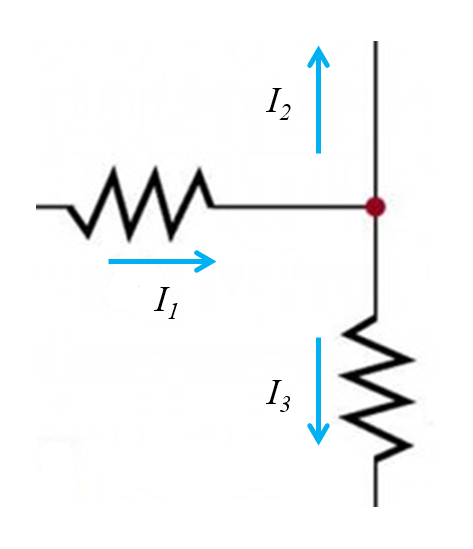
se tiene que

$I_1 = I_2 + I_3$

En ese sentido, teniendo presente de que las que salen son negativas (se restan de las que entran), la suma de estas deben ser nulas. Esta condici n se conoce como la primera ley de Kirchhoff.

(ID 12062)

La suma de los potenciales a lo largo de cada loop o ciclo debe ser nula en funci n de que la energ a se conserva. Esto significa que:

- Las resistencias contribuyen multiplicando la resistencia con la respectiva corriente. El signo del termino sera positivo depende de que la corriente fluya en el mismo sentido que la direcci n en que se esta analizado. Si se oponen el elemento contribuye con un signo negativo.

- Para el caso de la bater a se toma el potencial aportado y el signo se escoge de modo de que sera positivo si el flujo es en el sentido del an lisis y la corriente emana del polo negativo (el que tiene la barra mas corta) o si el sentido es opuesto pero tambi n la corriente emana del polo positivo. En el caso contrario el signo de la contribuci n es negativo.

Esto se resume en el siguiente diagrama:

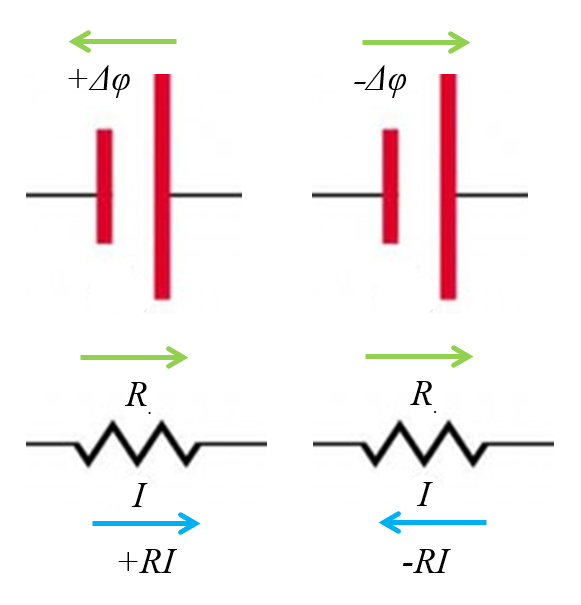
(ID 12064)

Como primer paso:

- identifique los notos, o sea puntos en que hay tres o mas contactos

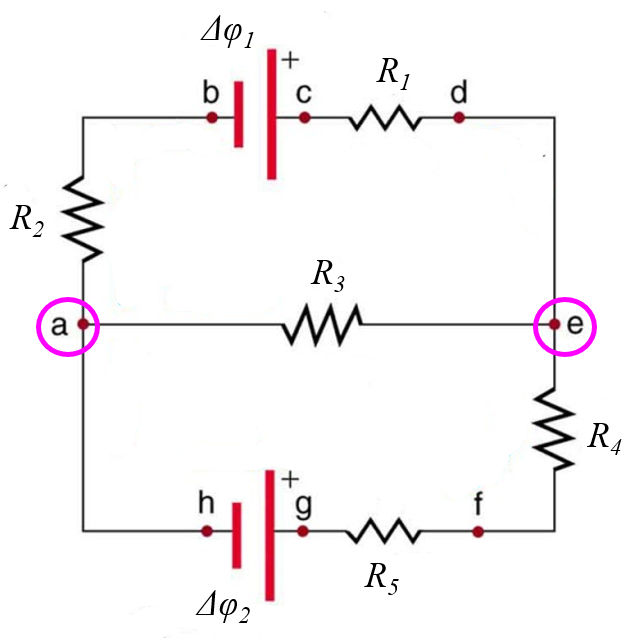
(ID 12065)

Como segundo paso:

- asigne variables para las distintas corrientes

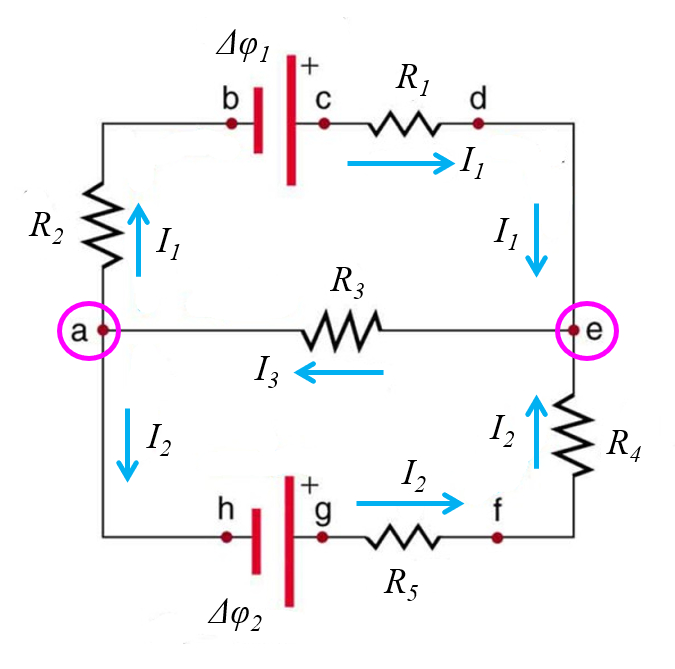
Para ello tenga en cuenta que las cargas se conservan por lo que muchos segmentos deben tener necesariamente corrientes ya definidas en otros.

Para cada nodo escriba la ecuaci n seg n la primera ley de Kirchhoff, es decir que la suma de las corrientes debe ser nula. Es posible que ecuaciones se repitan por efecto de que los ciclos se cierran.

(ID 12066)

Dentro del circuito los nodos generan 'celdas' cerradas que se deben identificar se alando en el sentido que se analizar n:

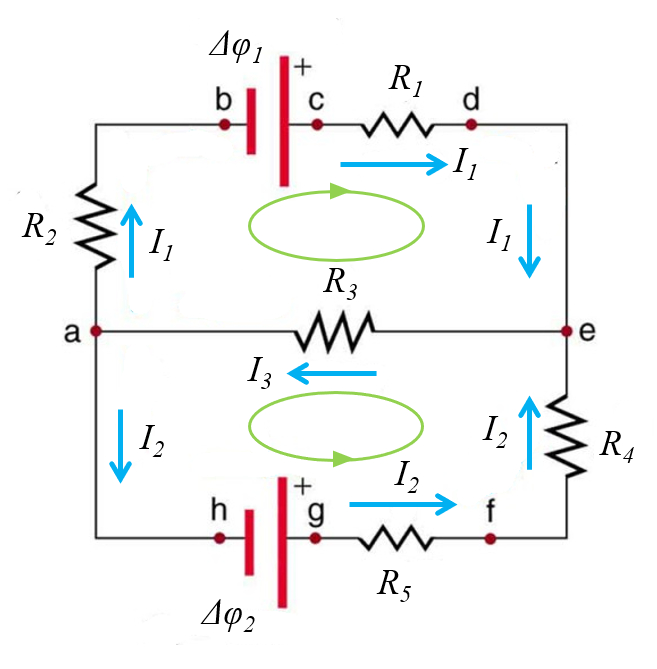
Nota: el resultado final no depende del sentido que se escoja para realizar el an lisis.

En el presente caso la suma es para el primer ciclo:

$R_2I_1 - \Delta\varphi_1 + R_1I_1 + R_3I_3 = 0 $

y para el segundo ciclo

$R_3I_3 - \Delta\varphi_2 +R_5I_2 +R_4I_2 = 0$

(ID 12067)

Otro ejemplo de circuito que se puede analizar se observa en el siguiente diagrama:

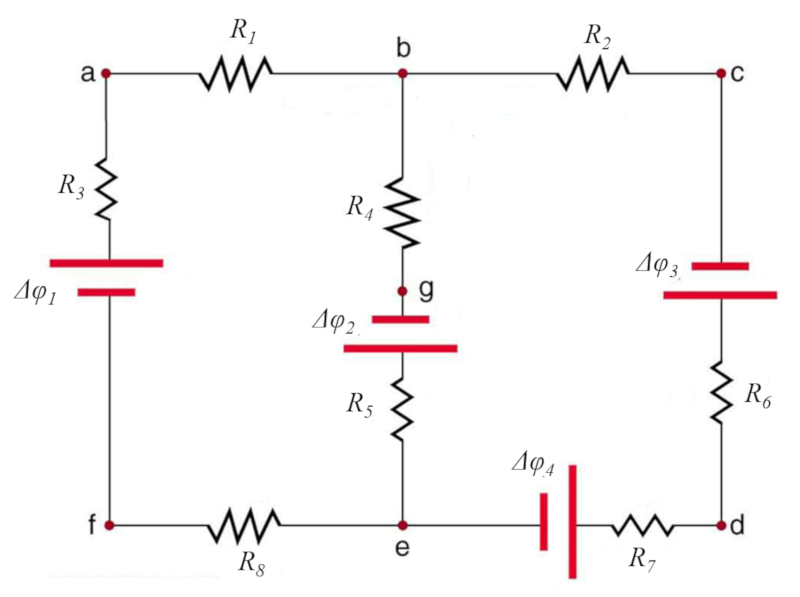
(ID 12068)

La soluci n tiene la siguiente forma:

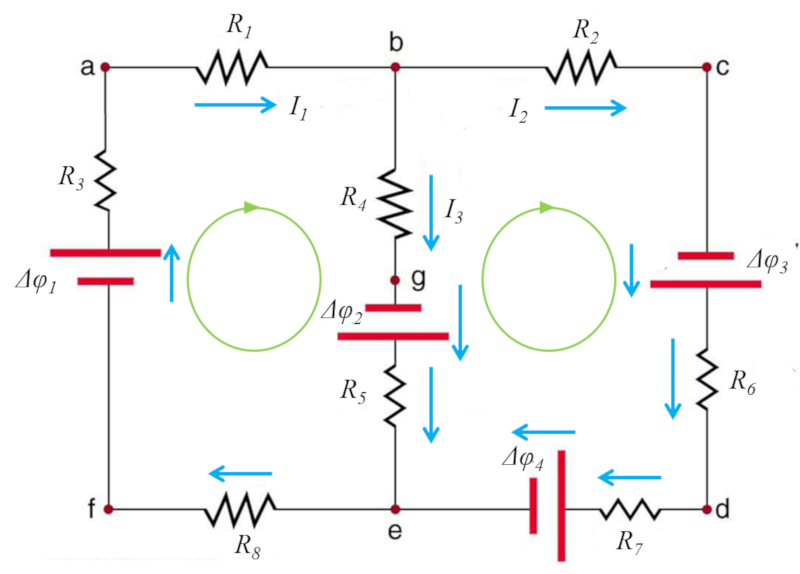
Las ecuaciones que aqu se determinan son:

- la de conservaci n de cargas

$I_1 = I_2 + I_3$

- la conservaci n de energ a en el primer ciclo

$R_1I_1 + R_4I_3 - \Delta\varphi_2 + R_8I_1 - \Delta\varphi_1 = 0$

- y el segundo ciclo

$R_2I_2 - \Delta\varphi_3 + I_2R_7 +\Delta\varphi_4 - R_5I_3 -\Delta\varphi_2 - R_4I_3 =0$

(ID 12069)

Este es un ejemplo con tres celdas

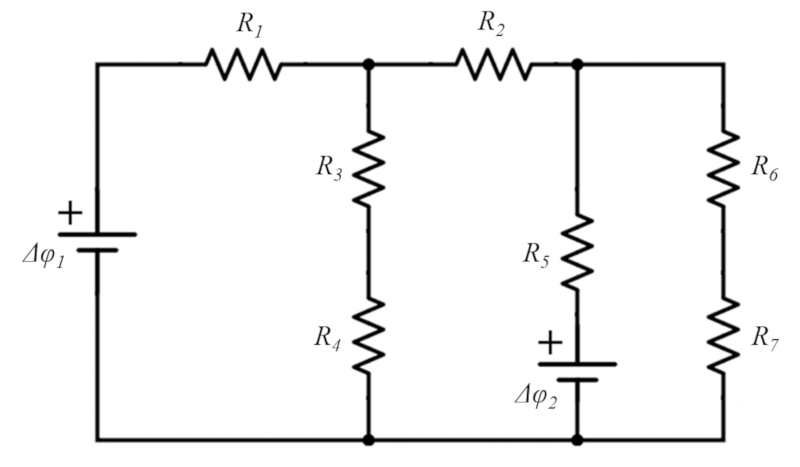
(ID 12070)