Ohmsches Gesetz
Storyboard 
Wenn ein Feld an eine Last angelegt wird, wird eine Kraft erhalten. Eine solche Kraft, die entlang eines Pfades ausgeübt wird, führt zu potentieller Energie. Wird es durch ein elektrisches Feld ausgedrückt, erhält man die potentielle Energie pro Ladung, die wir elektrisches Potential nennen. Das elektrische Potential erzeugt eine Verschiebung von Ladungen, was impliziert, dass es einen Fluss gibt, den wir elektrischen Strom nennen. Ihre Größe hängt von dem elektrischen Potential und dem Widerstand des Materials ab, in dem sich die Elektronen befinden, die wir den Leiter nennen werden. Das resultierende Gesetz ist das sogenannte Ohmsche Gesetz.
ID:(815, 0)
Strom durch einen Leiter
Bild 
Zusammenfassend lässt sich sagen, dass durch Anlegen einer Potentialdifferenz zwischen den beiden Enden des Leiters
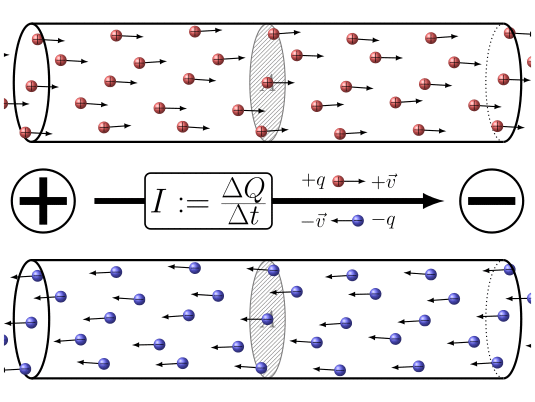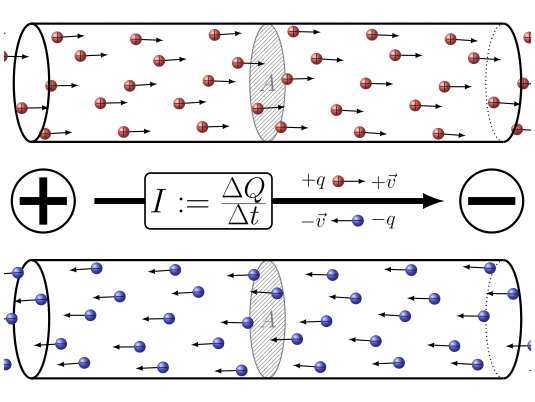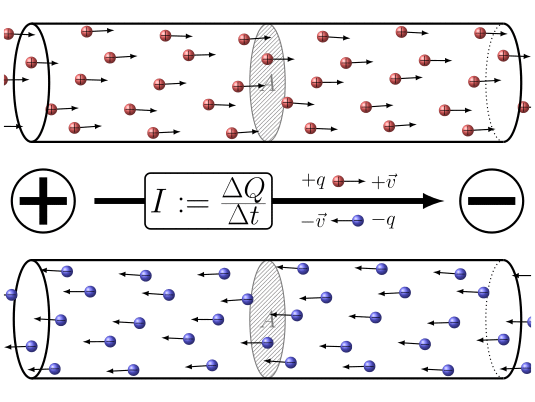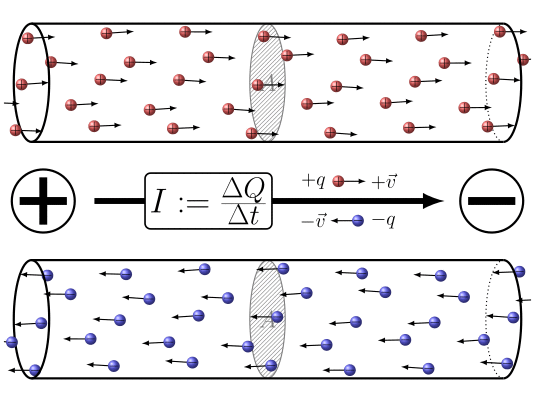
ID:(7860, 0)
Widerstand und Hitze
Bild 
Die Hitze lässt die Atome mit einer größeren Amplitude schwingen, was es den Elektronen erschwert, voranzukommen:
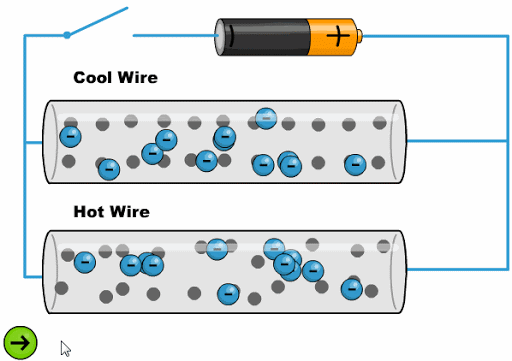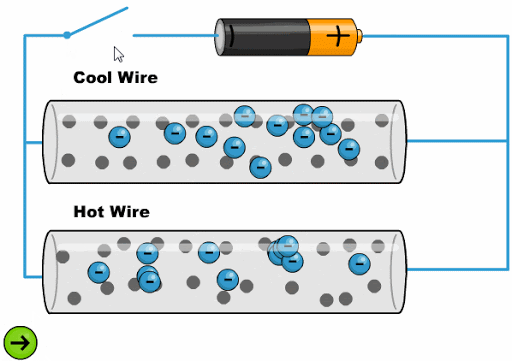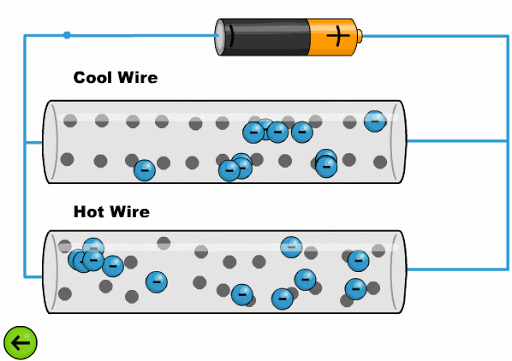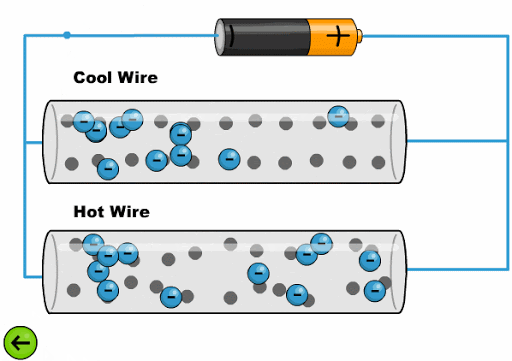
ID:(11761, 0)
Ohmsches Gesetz
Beschreibung 
Wenn ein Feld auf eine Ladung angewendet wird, entsteht eine Kraft. Diese Kraft führt, wenn sie entlang eines Weges wirkt, zu einer potenziellen Energie. Wenn diese potenzielle Energie in Bezug auf ein elektrisches Feld ausgedrückt wird, erhält man die potenzielle Energie pro Ladungseinheit, die als elektrisches Potenzial bekannt ist. Das elektrische Potenzial bewirkt die Bewegung von Ladungen, was einen Fluss erzeugt, der als elektrischer Strom bezeichnet wird. Die Größe dieses Stroms hängt sowohl vom angelegten elektrischen Potenzial als auch vom Widerstand des Materials ab, durch das sich die Ladungen bewegen, das üblicherweise als Leiter bezeichnet wird. Die daraus resultierende Beziehung zwischen elektrischem Potenzial, Strom und Widerstand wird durch das bekannte Ohmsche Gesetz beschrieben.
Variablen
Berechnungen
Berechnungen
Gleichungen
None
(ID 3214)
None
(ID 3843)
(ID 10400)
None
(ID 10401)
(ID 16236)
Beispiele
(ID 16003)
Zusammenfassend l sst sich sagen, dass durch Anlegen einer Potentialdifferenz zwischen den beiden Enden des Leiters

(ID 7860)
Die Hitze l sst die Atome mit einer gr eren Amplitude schwingen, was es den Elektronen erschwert, voranzukommen:

(ID 11761)
(ID 16002)
ID:(815, 0)
