Utilisateur:
Loi d'Ohm
Description 
Lorsquun champ est appliqué à une charge, il génère une force. Cette force, en agissant le long dun chemin, donne naissance à une énergie potentielle. Si cette énergie potentielle est exprimée en termes de champ électrique, elle devient l'énergie potentielle par unité de charge, connue sous le nom de potentiel électrique. Le potentiel électrique induit le déplacement des charges, créant un flux appelé courant électrique. La magnitude de ce courant dépend à la fois du potentiel électrique appliqué et de la résistance du matériau à travers lequel les charges se déplacent, communément appelé conducteur. La relation résultante entre le potentiel électrique, le courant et la résistance est décrite par la célèbre loi dOhm.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
(ID 3214)
(ID 10400)
(ID 16236)
Exemples
(ID 16003)
El calor hace que los tomos oscila con una mayor amplitud dificultando el avance de los electrones:
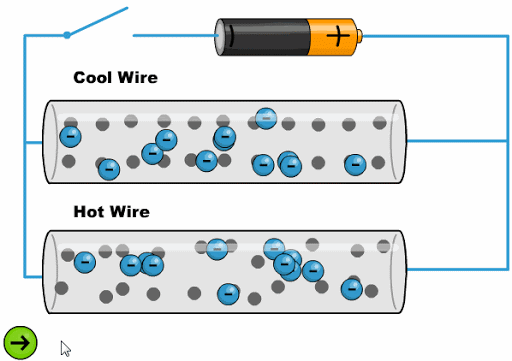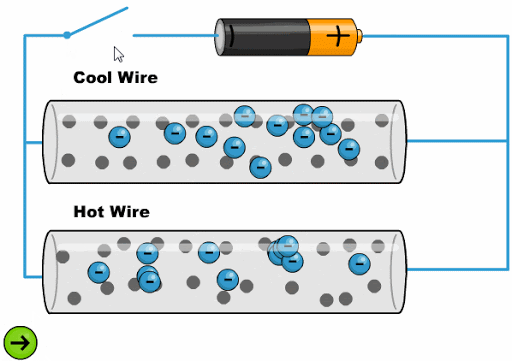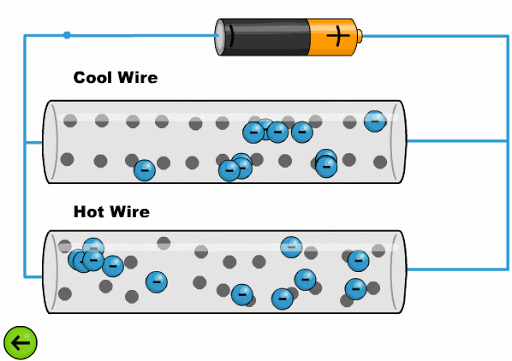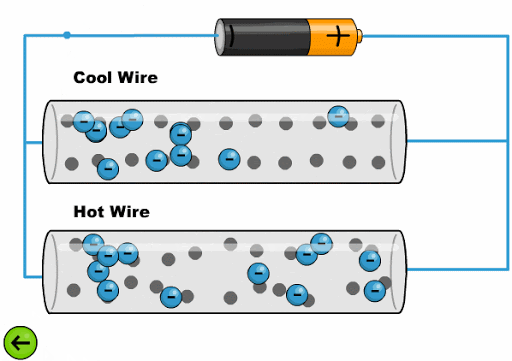
(ID 11761)
(ID 16002)
Lorsque des charges lectriques se d placent, il est possible de d finir une quantit a elément de charge ($\Delta Q$), qui repr sente la quantit de charge traversant une section pendant un intervalle de temps le temps écoulé ($\Delta t$). Cette quantit est li e une courant ($I$) et est d finie par l'expression suivante :
| $ I =\displaystyle\frac{ \Delta Q }{ \Delta t }$ |
(ID 10401)
Le champ électrique ($E$) est g n r par a différence potentielle ($\Delta\varphi$) entre deux lectrodes, s par es par une distance de un longueur du pilote ($L$). Cette valeur peut tre calcul e laide de lexpression suivante :
| $ E =\displaystyle\frac{ \Delta\varphi }{ L }$ |
(ID 3838)
A vitesse maximum ($v_{max}$) est atteint en moyenne lorsque lélectron est accéléré avec a accélération des charges sur le conducteur ($a$) pendant lintervalle de temps le temps entre les collisions ($\tau$), ce qui donne :
| $ v_{max} = a \tau $ |
(ID 16236)
Le champ électrique ($E$), associ a charge électronique ($e$), g n re une force qui, travers a masse électronique ($m_e$), aboutit a accélération des charges sur le conducteur ($a$). Cette relation peut tre exprim e comme suit :
| $ a =\displaystyle\frac{ e E }{ m_e }$ |
(ID 3843)
En un temps entre les collisions ($\tau$), l' lectron est acc l r par le champ électrique ($E$), en combinaison avec a charge électronique ($e$) et a masse électronique ($m_e$), jusqu' atteindre a vitesse maximum ($v_{max}$). Ce processus est d crit par la relation suivante :
| $ v_{max} =\displaystyle\frac{ e E }{ m_e } \tau $ |
(ID 3836)
Comme lélectron subit une accélération uniforme, sa vitesse augmente linéairement avec le temps jusquà atteindre a vitesse maximum ($v_{max}$). Par conséquent, la vitesse moyenne a vitesse moyenne des charges ($\bar{v}$) est :
| $ \overline{v} =\displaystyle\frac{1}{2} v_{max} $ |
(ID 16237)
A courant ($I$) peut tre calcul en consid rant des lectrons avec une concentration de charge ($c$) et a charge électronique ($e$), se d pla ant une vitesse moyenne des charges ($\bar{v}$) travers une espace conducteur ($S$). Cette relation sexprime comme suit :
| $ I = e S c \bar{v} $ |
(ID 10400)
A courant ($I$) peut tre calcul partir de le champ électrique ($E$), en combinaison avec a charge électronique ($e$), a concentration de charge ($c$), a masse électronique ($m_e$), le temps entre les collisions ($\tau$) et a espace conducteur ($S$), en utilisant la relation suivante :
| $ I =\displaystyle\frac{ e ^2 E }{2 m_e } \tau c S $ |
(ID 3837)
Si a courant ($I$) est exprim en utilisant a différence potentielle ($\Delta\varphi$) au lieu de le champ électrique ($E$), on obtient la forme microscopique de la loi d'Ohm. Cette quation implique a charge électronique ($e$), a concentration de charge ($c$), a masse électronique ($m_e$), le temps entre les collisions ($\tau$), a espace conducteur ($S$) et le longueur du pilote ($L$), travers la relation suivante :
| $ \Delta\varphi =\displaystyle\frac{2 m_e }{ e ^2 \tau c }\displaystyle\frac{ L }{ S } I $ |
(ID 3839)
partir de la forme microscopique de la loi d'Ohm, on peut identifier un facteur sp cifique au mat riau du conducteur. Cela permet de d finir a résistivité ($\rho_e$) en fonction de a charge électronique ($e$), a concentration de charge ($c$), a masse électronique ($m_e$) et le temps entre les collisions ($\tau$), en utilisant la relation suivante :
| $ \rho_e =\displaystyle\frac{2 m_e }{ e ^2 \tau c }$ |
(ID 3840)
En utilisant a résistivité ($\rho_e$) ainsi que les param tres g om triques le longueur du pilote ($L$) et a espace conducteur ($S$), a résistance ($R$) peut tre d fini travers la relation suivante :
| $ R = \rho_e \displaystyle\frac{ L }{ S }$ |
(ID 3841)
La loi d'Ohm traditionnelle tablit une relation entre a différence potentielle ($\Delta\varphi$) et a courant ($I$) via a résistance ($R$), en utilisant l'expression suivante :
| $ \Delta\varphi = R I $ |
(ID 3214)
ID:(815, 0)