Kirchhoffs Gesetze
Storyboard 
Für komplexere Schaltkreise von Energiequellen und Widerständen können die sogenannten Kirchhoffschen Gesetze verwendet werden, um die verschiedenen Ströme zu berechnen, die in den verschiedenen Abschnitten auftreten.
ID:(1621, 0)
Ziel: Ströme in einem Stromkreis bestimmen
Definition 
Cuando estudiamos un circuito podemos determinar en forma directa las respectivas resistencias y potenciales de las fuentes (ej. baterias). Todos estos parámetros determinan como la corriente fluirá por el sistema. Esto se puede medir, si existe el circuito, o calcular, cuando se esta diseñado y aun no se cuenta con el sistema físicamente.
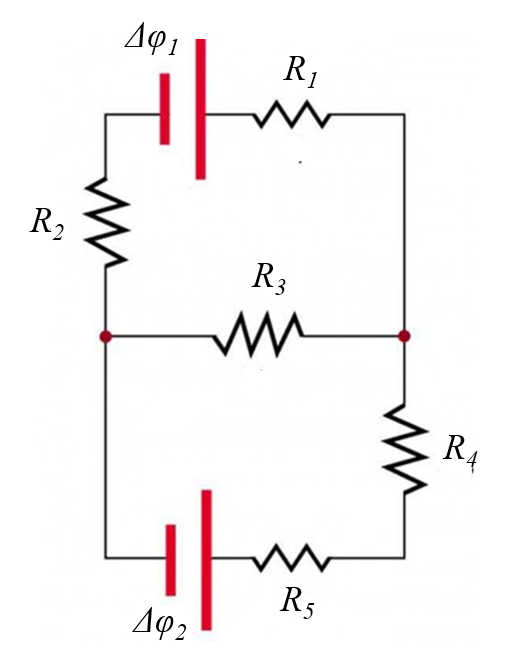
La pregunta es como se pueden calcular dichas corrientes.
ID:(12060, 0)
Definieren Sie die zu ermittelnden Variablen
Bild 
Para determinar las corrientes debemos primero definir aquellas que pueden existir.
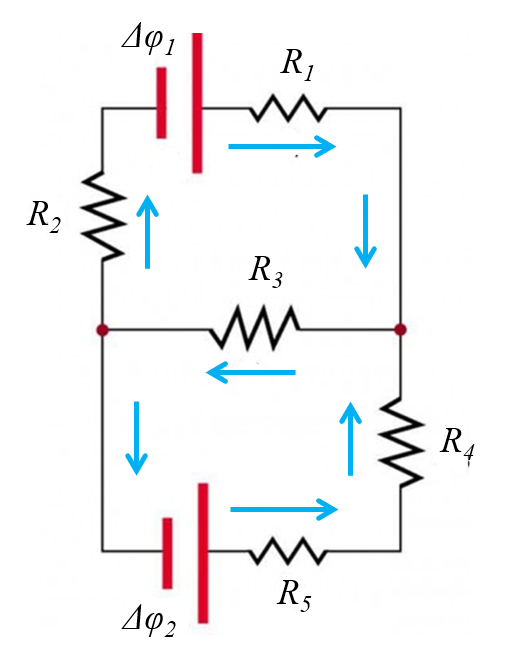
Para ello se debe comprender que las cargas se conservan, por lo que la corriente:
No varia a lo largo de una secuencia de elementos que no tienen otro conector
En cada bifurcación la suma total de flujos debe ser nula (o sea entran tantos electrones como salen)
ID:(12061, 0)
Zustand an jedem Knoten
Notiz 
En cada nodo las corrientes que arriban deben en suma ser iguales a la suma de las que salen. En el caso de la imagen
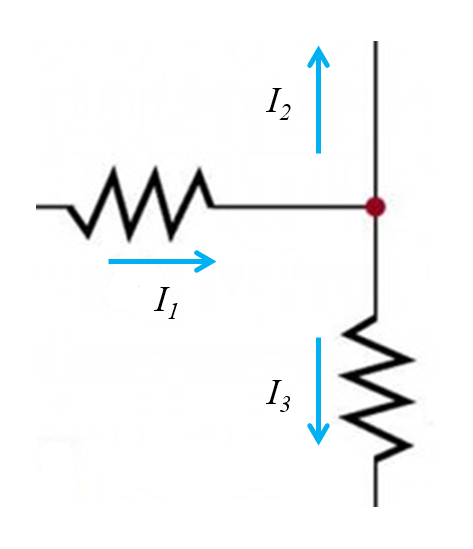
se tiene que
$I_1 = I_2 + I_3$
En ese sentido, teniendo presente de que las que salen son negativas (se restan de las que entran), la suma de estas deben ser nulas. Esta condición se conoce como la primera ley de Kirchhoff.
ID:(12062, 0)
Energieeinsparung
Zitat 
La suma de los potenciales a lo largo de cada loop o ciclo debe ser nula en función de que la energía se conserva. Esto significa que:
- Las resistencias contribuyen multiplicando la resistencia con la respectiva corriente. El signo del termino sera positivo depende de que la corriente fluya en el mismo sentido que la dirección en que se esta analizado. Si se oponen el elemento contribuye con un signo negativo.
- Para el caso de la batería se toma el potencial aportado y el signo se escoge de modo de que sera positivo si el flujo es en el sentido del análisis y la corriente emana del polo negativo (el que tiene la barra mas corta) o si el sentido es opuesto pero también la corriente emana del polo positivo. En el caso contrario el signo de la contribución es negativo.
Esto se resume en el siguiente diagrama:
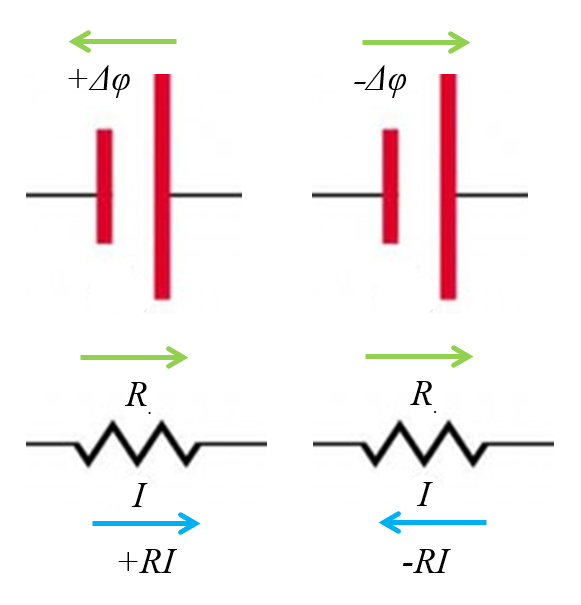
ID:(12064, 0)
Analyseprozess: Knoten identifizieren
Übung 
Como primer paso:
- identifique los notos, o sea puntos en que hay tres o mas contactos
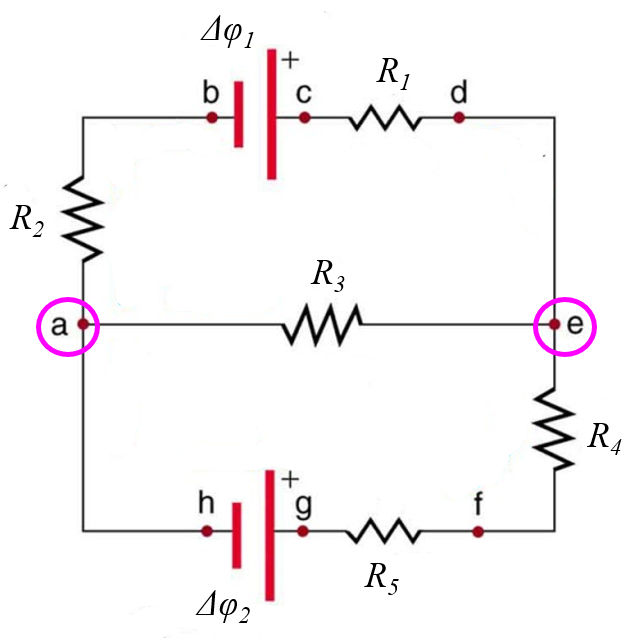
ID:(12065, 0)
Analyseprozess: Strömungen definieren
Gleichung 
Como segundo paso:
- asigne variables para las distintas corrientes
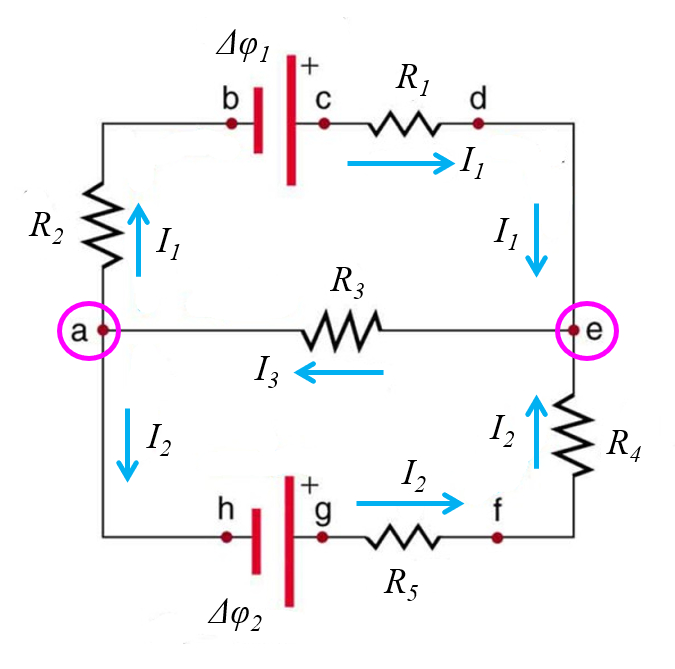
Para ello tenga en cuenta que las cargas se conservan por lo que muchos segmentos deben tener necesariamente corrientes ya definidas en otros.
Para cada nodo escriba la ecuación según la primera ley de Kirchhoff, es decir que la suma de las corrientes debe ser nula. Es posible que ecuaciones se repitan por efecto de que los ciclos se cierran.
ID:(12066, 0)
Analyseprozess: Definieren Sie die Zellen und die Richtung, in der Sie sie analysieren möchten
Script 
Dentro del circuito los nodos generan 'celdas' cerradas que se deben identificar señalando en el sentido que se analizarán:
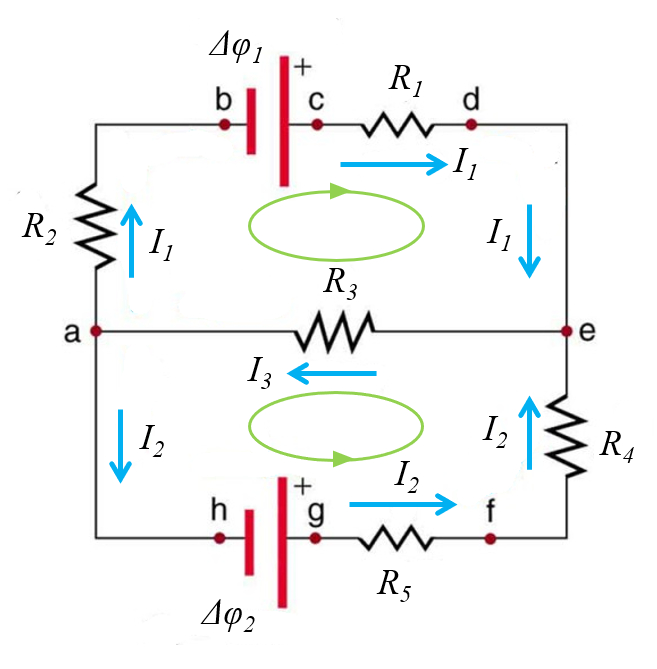
Nota: el resultado final no depende del sentido que se escoja para realizar el análisis.
En el presente caso la suma es para el primer ciclo:
$R_2I_1 - \Delta\varphi_1 + R_1I_1 + R_3I_3 = 0 $
y para el segundo ciclo
$R_3I_3 - \Delta\varphi_2 +R_5I_2 +R_4I_2 = 0$
ID:(12067, 0)
Ein anderes Beispiel
Variable 
Otro ejemplo de circuito que se puede analizar se observa en el siguiente diagrama:
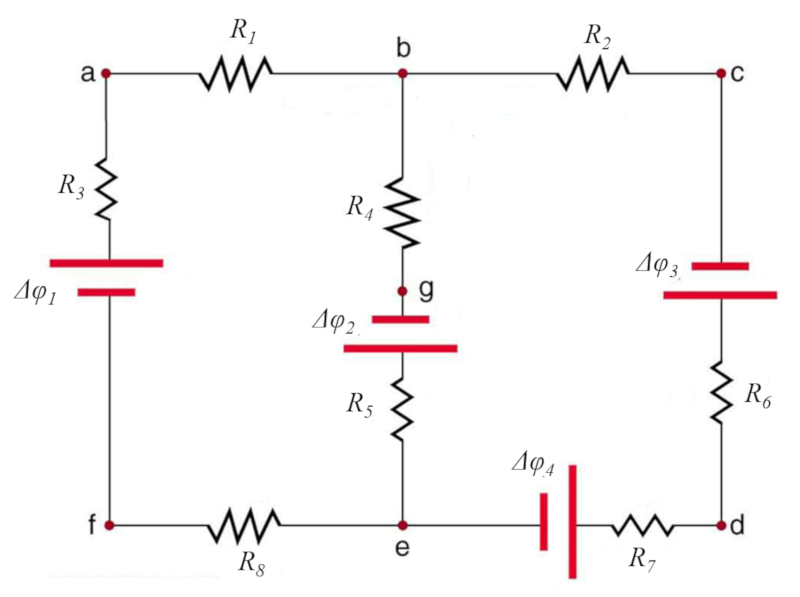
ID:(12068, 0)
Lösungsstruktur
Audio 
La solución tiene la siguiente forma:
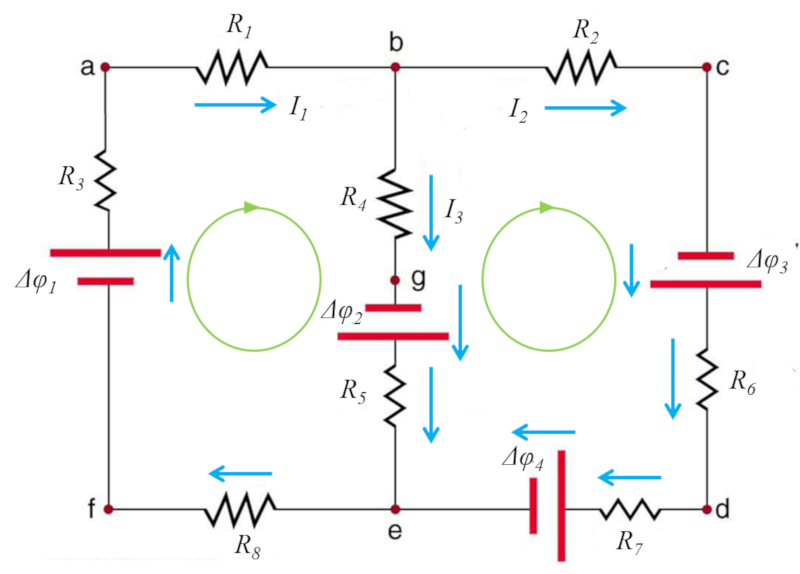
Las ecuaciones que aquí se determinan son:
- la de conservación de cargas
$I_1 = I_2 + I_3$
- la conservación de energía en el primer ciclo
$R_1I_1 + R_4I_3 - \Delta\varphi_2 + R_8I_1 - \Delta\varphi_1 = 0$
- y el segundo ciclo
$R_2I_2 - \Delta\varphi_3 + I_2R_7 +\Delta\varphi_4 - R_5I_3 -\Delta\varphi_2 - R_4I_3 =0$
ID:(12069, 0)
Kirchhoffs Gesetze
Beschreibung 
Für komplexere Schaltkreise von Energiequellen und Widerständen können die sogenannten Kirchhoffschen Gesetze verwendet werden, um die verschiedenen Ströme zu berechnen, die in den verschiedenen Abschnitten auftreten.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Cuando estudiamos un circuito podemos determinar en forma directa las respectivas resistencias y potenciales de las fuentes (ej. baterias). Todos estos par metros determinan como la corriente fluir por el sistema. Esto se puede medir, si existe el circuito, o calcular, cuando se esta dise ado y aun no se cuenta con el sistema f sicamente.

La pregunta es como se pueden calcular dichas corrientes.
(ID 12060)
Para determinar las corrientes debemos primero definir aquellas que pueden existir.

Para ello se debe comprender que las cargas se conservan, por lo que la corriente:
No varia a lo largo de una secuencia de elementos que no tienen otro conector
En cada bifurcaci n la suma total de flujos debe ser nula (o sea entran tantos electrones como salen)
(ID 12061)
En cada nodo las corrientes que arriban deben en suma ser iguales a la suma de las que salen. En el caso de la imagen

se tiene que
$I_1 = I_2 + I_3$
En ese sentido, teniendo presente de que las que salen son negativas (se restan de las que entran), la suma de estas deben ser nulas. Esta condici n se conoce como la primera ley de Kirchhoff.
(ID 12062)
La conservaci n de las cargas el ctricas implica que la suma de todas las corrientes que entran y salen de un nodo deben ser nulas. Con
| $ \displaystyle\sum_i I_i = 0$ |
(ID 12063)
La suma de los potenciales a lo largo de cada loop o ciclo debe ser nula en funci n de que la energ a se conserva. Esto significa que:
- Las resistencias contribuyen multiplicando la resistencia con la respectiva corriente. El signo del termino sera positivo depende de que la corriente fluya en el mismo sentido que la direcci n en que se esta analizado. Si se oponen el elemento contribuye con un signo negativo.
- Para el caso de la bater a se toma el potencial aportado y el signo se escoge de modo de que sera positivo si el flujo es en el sentido del an lisis y la corriente emana del polo negativo (el que tiene la barra mas corta) o si el sentido es opuesto pero tambi n la corriente emana del polo positivo. En el caso contrario el signo de la contribuci n es negativo.
Esto se resume en el siguiente diagrama:

(ID 12064)
La conservaci n de energ a se da en cada subsistema cerrado. En el la suma de las diferencias de potencial el ctrico generados por fuentes y por resistencias mediante la ley de Ohm que con es
| $ \Delta\varphi = R I $ |
Dentro de esta suma eso si se debe respetar la direcci n en que se van sumando las contribuciones. Para ello vale:
- las resistencias contribuyen en forma positiva si la direcci n en que se van sumando coincide con la direcci n del flujo de la corriente, de lo contrario contribuyen en forma negativa
- las fuentes contribuyen en forma positiva si est n polarizadas (positivo > negativo) en la misma direcci n que la direcci n de suma, de lo contrario en forma negativa
Con la condici n de considerar los signos de las diferencias de potenciales y corrientes se tiene que la segunda ley de Kirchhoff es con igual a
| $ \displaystyle\sum_i \Delta\varphi_i + \displaystyle\sum_i R_i I_i = 0 $ |
(ID 12081)
Como primer paso:
- identifique los notos, o sea puntos en que hay tres o mas contactos

(ID 12065)
Como segundo paso:
- asigne variables para las distintas corrientes

Para ello tenga en cuenta que las cargas se conservan por lo que muchos segmentos deben tener necesariamente corrientes ya definidas en otros.
Para cada nodo escriba la ecuaci n seg n la primera ley de Kirchhoff, es decir que la suma de las corrientes debe ser nula. Es posible que ecuaciones se repitan por efecto de que los ciclos se cierran.
(ID 12066)
Dentro del circuito los nodos generan 'celdas' cerradas que se deben identificar se alando en el sentido que se analizar n:

Nota: el resultado final no depende del sentido que se escoja para realizar el an lisis.
En el presente caso la suma es para el primer ciclo:
$R_2I_1 - \Delta\varphi_1 + R_1I_1 + R_3I_3 = 0 $
y para el segundo ciclo
$R_3I_3 - \Delta\varphi_2 +R_5I_2 +R_4I_2 = 0$
(ID 12067)
Otro ejemplo de circuito que se puede analizar se observa en el siguiente diagrama:

(ID 12068)
La soluci n tiene la siguiente forma:

Las ecuaciones que aqu se determinan son:
- la de conservaci n de cargas
$I_1 = I_2 + I_3$
- la conservaci n de energ a en el primer ciclo
$R_1I_1 + R_4I_3 - \Delta\varphi_2 + R_8I_1 - \Delta\varphi_1 = 0$
- y el segundo ciclo
$R_2I_2 - \Delta\varphi_3 + I_2R_7 +\Delta\varphi_4 - R_5I_3 -\Delta\varphi_2 - R_4I_3 =0$
(ID 12069)
Este es un ejemplo con tres celdas
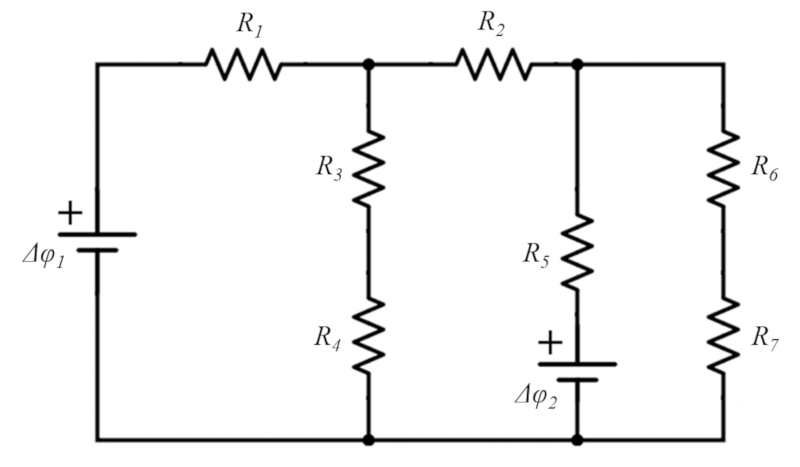
(ID 12070)
ID:(1621, 0)
