Usuario:


Uso de Capacitancias
Storyboard

Las capacitancias son placas metálicas a corta distancia que se pueden cargar conectando a una diferencia de potencial. De esta forma se tiene una placa con cargas negativas (electrones) y la otra positivas (faltas de electrones por lo que predominan las cargas positivas de la estructura del conductor) que se mantienen en sus lugares por la atracción entre cargas de distinto signo. Una vez se conectan ambos polos mediante un conductor circula corriente hasta que se descargo completamente igualándose la carga en ambas placas.

>Modelo

ID:(816, 0)


Dos placas con cargas opuestas
Definición

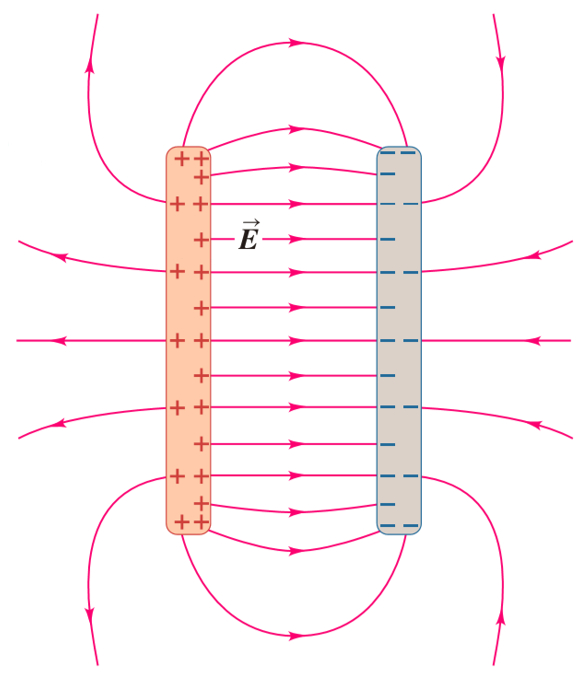
En el caso de dos placas con cargas opuestas existe un campo de mayor intensidad entre estas. Sin embargo existe un campo menor que se puede describir con lineas de campo que surjan de una de las placas y vuelven dando una vuelta externa a la placa opuesta:

ID:(11454, 0)


Uso de Capacitancias
Descripción

Las capacitancias son placas metálicas a corta distancia que se pueden cargar conectando a una diferencia de potencial. De esta forma se tiene una placa con cargas negativas (electrones) y la otra positivas (faltas de electrones por lo que predominan las cargas positivas de la estructura del conductor) que se mantienen en sus lugares por la atracción entre cargas de distinto signo. Una vez se conectan ambos polos mediante un conductor circula corriente hasta que se descargo completamente igualándose la carga en ambas placas.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$C$
C
Capacidad del capacitor
F
$Q$
Q
Carga
C
$\epsilon$
epsilon
Constante dieléctrica
-
$\Delta\varphi$
Dphi
Diferencia de potencial
V
$d$
d
Distancia entre placas
m
$S$
S
Superficie de placas
m^2

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

En el caso de dos placas con cargas opuestas existe un campo de mayor intensidad entre estas. Sin embargo existe un campo menor que se puede describir con lineas de campo que surjan de una de las placas y vuelven dando una vuelta externa a la placa opuesta:

(ID 11454)

Si se define una superficie que pasa entre las placas y rodea la carga Q se puede aplicar la ley de Gauss para calcular el campo que se forma entre las placas. Si se asume que el campo solo existe entre las dos placas y estas tienen una superficie S se obtiene que

$E_dS=\displaystyle\frac{Q}{\epsilon\epsilon_0}$



con \epsilon_0 la constante de campo y \epsilon el n mero diel ctrico.

Como por otro lado el campo es igual a la diferencia de potencial \Delta\varphi partido por la distancia entre las placas d se obtiene

$\Delta\varphi = \displaystyle\frac{\sigma}{\epsilon\epsilon_0}d=E_dd=\displaystyle\frac{Q}{\epsilon\epsilon_0}\displaystyle\frac{d}{S}$



se obtiene con la definici n

$\Delta\varphi=\displaystyle\frac{Q}{C}$



que la capacidad de dos placas se puede calcular con

$ C = \epsilon_0 \epsilon \displaystyle\frac{ S }{ d }$

(ID 3865)

La diferencia de potencial ($\Delta\varphi$) genera la carga en el condensador, induciendo la acumulaci n de la carga ($Q$) en cada lado (con signos opuestos), dependiendo de la capacidad del capacitor ($C$), de acuerdo con la siguiente relaci n:

$ \Delta\varphi =\displaystyle\frac{ Q }{ C }$

(ID 3864)

ID:(816, 0)