Utilizador:
Controle de rolagem
Storyboard 
O controle de rolamento é o mecanismo que permite à aeronave girar em torno de seu eixo longitudinal, elevando uma asa enquanto abaixa a outra. Esse controle é obtido gerando uma diferença de sustentação através dos ailerons, localizados nas extremidades das asas. Essa diferença de sustentação cria um torque, responsável por fazer a aeronave rolar ao redor de um eixo imaginário ao longo do fuselagem, conhecido como eixo de rolamento.
ID:(2114, 0)
Controle de rolagem
Conceito
Para realizar um rolamento em torno do seu eixo, a aeronave utiliza os ailerons. Estes geram uma força nos ailerons ($F_a$) que, em conjunto com uma centro de distância de massa e ailerons ($d_a$), induzem um torque gerado pelos ailerons ($T_a$). Os ailerons estão localizados nas pontas das asas da aeronave para maximizar sua la centro de distância de massa e ailerons ($d_a$) em relação ao centro de massa e obter uma maior uma centro de distância de massa e elevadores ($d_e$).
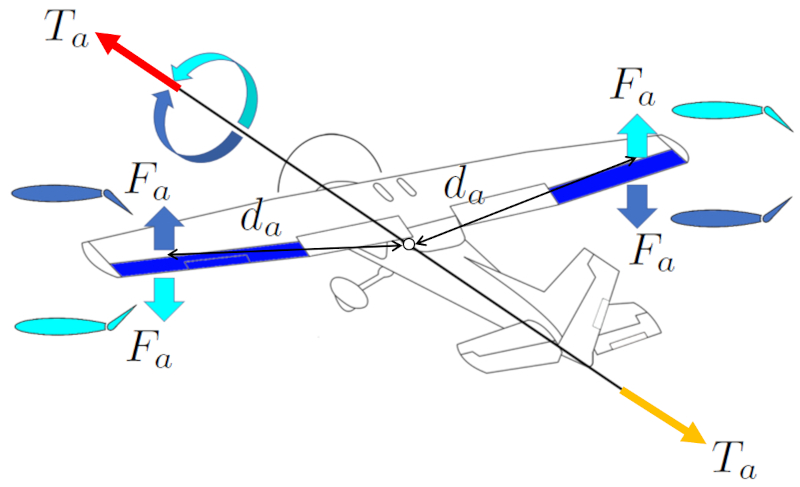
Os ailerons operam de maneira assimétrica, o que significa que se o aileron da asa direita gera sustentação para cima, o da asa esquerda faz o oposto, e vice-versa. Dessa forma, essas forças geram um torque que permite girar no sentido horário ou anti-horário.
O objetivo da rotação é gerar, com a força de sustentação, uma força ortogonal ao eixo central, resultando em uma curva na aeronave. Isso reforça a ação do leme, auxiliando na manobra de viragem da aeronave. De fato, essa é a forma como as aves realizam suas manobras de viragem, já que não possuem um leme.
Para realizar a manobra de viragem, o piloto utiliza o controle de coluna, que possui um volante que gira na mesma direção que a aeronave. Em outros casos, como no joystick das aeronaves Airbus, não há um volante, e o joystick é inclinado na direção desejada para realizar a curva.
Um dos problemas que surgem ao realizar uma rotação em torno do eixo central da aeronave é que a força de sustentação é utilizada para desviar a trajetória, resultando em uma diminuição da sustentação. Isso significa que, durante uma manobra de viragem, a aeronave e a ave tendem a perder altitude a menos que a potência seja aumentada.
ID:(15160, 0)
Momento de inércia para rolar
Descrição
O momento de inércia do eixo do avião ($I_a$) pode ser aproximado como o momento de inércia de um paralelepípedo retangular que representa a asa da aeronave, rotacionando em torno de um eixo paralelo à sua largura:
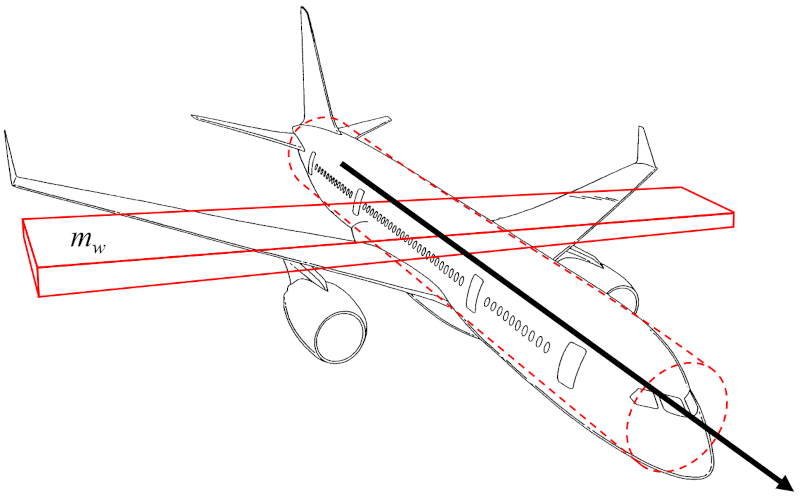
Como o corpo da aeronave é relativamente estreito, o momento de inércia do cilindro que o representa pode ser desprezado em uma primeira aproximação. Assim, o momento de inércia do eixo do avião ($I_a$) é proporcional a la massa da asa ($m_w$) e ao quadrado de la envergadura das asas ($L$).
Portanto, o momento de inércia do eixo do avião ($I_a$) é calculado a partir de la massa da asa ($m_w$) e la envergadura das asas ($L$), da seguinte forma:
 $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15992, 0)
Massa da asa
Descrição
La massa da asa ($m_w$) pode ser aproximado como o volume de um paralelepípedo retângulo multiplicado pela densidade da aeronave:
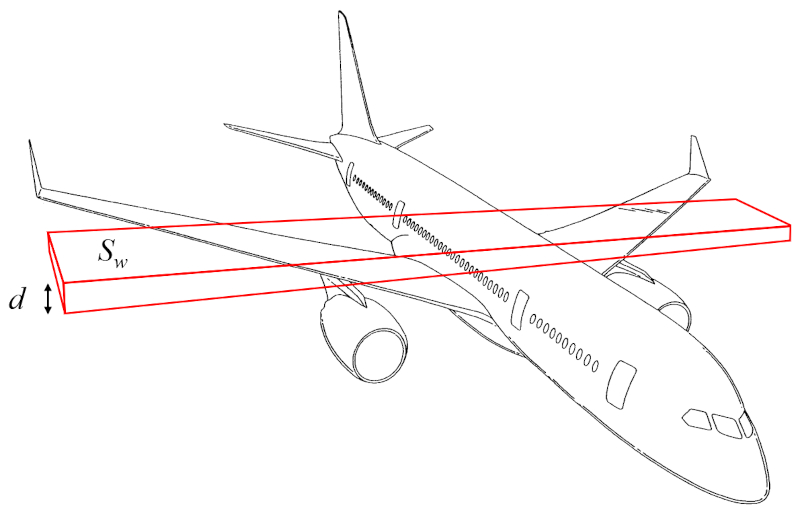
O volume, portanto, pode ser calculado a partir de la superfície que gera sustentação ($S_w$) e la altura da asa ($d$).
Assim, la massa da asa ($m_w$) é determinado utilizando o densidade corporal da aeronave ($\rho_a$), la superfície que gera sustentação ($S_w$) e la altura da asa ($d$), da seguinte maneira:
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Força gerada pelo rolamento
Equação
| $ T_a = d_a F_L $ |
 $ T_a = d_a F_a $ |
ID:(15164, 0)
Torque de rolamento
Equação
| $ T_a = I_a \alpha_a $ |
ID:(15167, 0)
Sustentação
Equação
Para gerar uma pressão maior abaixo do que acima da asa e gerar sustentação, utiliza-se o princípio de Bernoulli, corrigindo a falta de conservação da densidade de energia com um coeficiente de elevação ($C_L$). A pressão sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) através da seguinte fórmula:
| $ F_L =\displaystyle\frac{1}{2} \rho S_a C_L v ^2$ |
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
e para o coeficiente de elevação ($C_L$), definido como
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
obtemos
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Constante de elevação
Equação
A partir de medições, conclui-se que o coeficiente de sustentação $C_L$ é proporcional ao ângulo de ataque $\alpha$:
| $ C_L = c \alpha $ |
Após um certo ângulo, a curva diminui até chegar a zero. Isso ocorre porque acima desse ângulo crítico, os redemoinhos cobrem completamente a superfície superior da asa, levando à perda de sustentação. Esse fenômeno é conhecido como \"stall\" (estol em português).
ID:(4441, 0)
Momento de inércia para rolar
Equação
O momento de inércia do eixo do avião ($I_a$) é calculado a partir de la massa da asa ($m_w$) e ($$)6337
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15986, 0)
Massa da asa
Equação
La massa da asa ($m_w$) é calculado a partir de o densidade corporal da aeronave ($\rho_a$), la superfície que gera sustentação ($S_w$) e la altura da asa ($d$), da seguinte forma:
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Braço de força do aileron
Equação
La centro de distância de massa e ailerons ($d_a$) é definido como a metade de la envergadura das asas ($L$), expressado da seguinte maneira:
| $ d_a = \displaystyle\frac{ L }{2}$ |
ID:(15995, 0)
Relação espessura/espaço
Equação
O relação espessura/espaço ($\gamma_d$) é definido como a proporção de la altura da asa ($d$) para la envergadura das asas ($L$), representada da seguinte maneira:
| $ \gamma_d =\displaystyle\frac{ d }{ L }$ |
ID:(15976, 0)