Storyboard

O controle de arfagem é o mecanismo que permite levantar ou abaixar o nariz da aeronave, sendo essencial para o movimento de subida ou descida. Esse controle é realizado através da geração de sustentação pelos profundores, localizados nas pequenas asas próximas à cauda da aeronave. Essa força de sustentação gera um torque, responsável por fazer a aeronave girar em torno de um eixo imaginário, paralelo às asas principais, conhecido como eixo de arfagem.

>Modelo

ID:(2113, 0)

Iframe

>Top

ID:(15171, 0)

Conceito

>Top

Para inclinar o nariz da aeronave para cima ou para baixo, são utilizados os elevadores. Ambos são empregados de forma simétrica para gerar um efeito la força nos elevadores ($F_e$) simétrico. Colocando-os na cauda da aeronave, alcança-se uma ($$) maior eficácia ao posicioná-los próximo ao centro de massa. Isso proporciona controle suficiente para elevar ou baixar o nariz da aeronave.

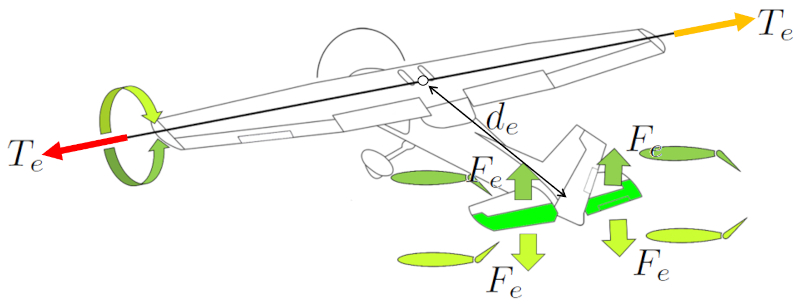
Em aeronaves mais antigas, o controle dos ailerons traseiros é realizado através de um manche, onde empurrar para a frente faz o nariz da aeronave descer, e puxar para trás eleva o nariz. Nas aeronaves da família Airbus, esse controle é feito com um joystick.

No caso das aves, existe uma solução semelhante, embora neste caso, a cauda não seja interrompida por um leme.

ID:(15161, 0)

Conceito

>Top

ID:(11079, 0)

Descrição

>Top

La massa da asa ($m_w$) pode ser aproximado como o volume de um paralelepípedo retângulo multiplicado pela densidade da aeronave:

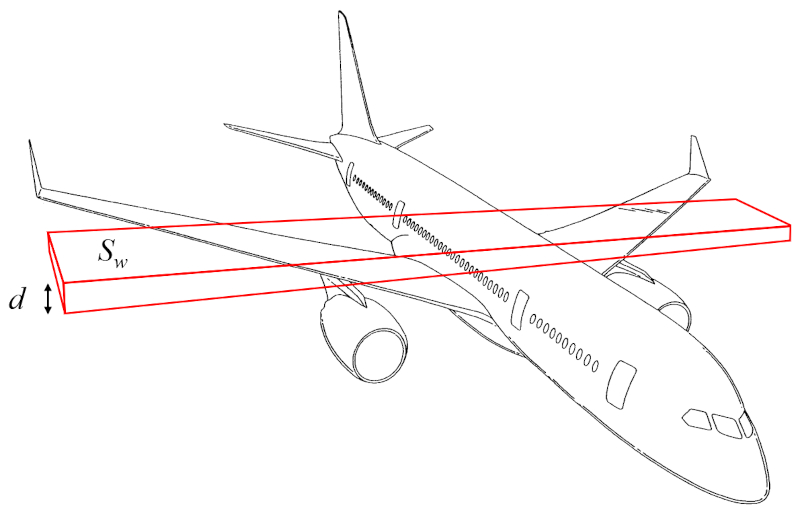
O volume, portanto, pode ser calculado a partir de la superfície que gera sustentação ($S_w$) e la altura da asa ($d$).

Assim, la massa da asa ($m_w$) é determinado utilizando o densidade corporal da aeronave ($\rho_a$), la superfície que gera sustentação ($S_w$) e la altura da asa ($d$), da seguinte maneira:

ID:(15989, 0)

Descrição

>Top

O momento de inércia do eixo da asa ($I_e$) pode ser aproximado como o momento de inércia de um cilindro que representa o corpo da aeronave, rotacionando em torno de um eixo perpendicular ao eixo do cilindro, que é paralelo às asas:

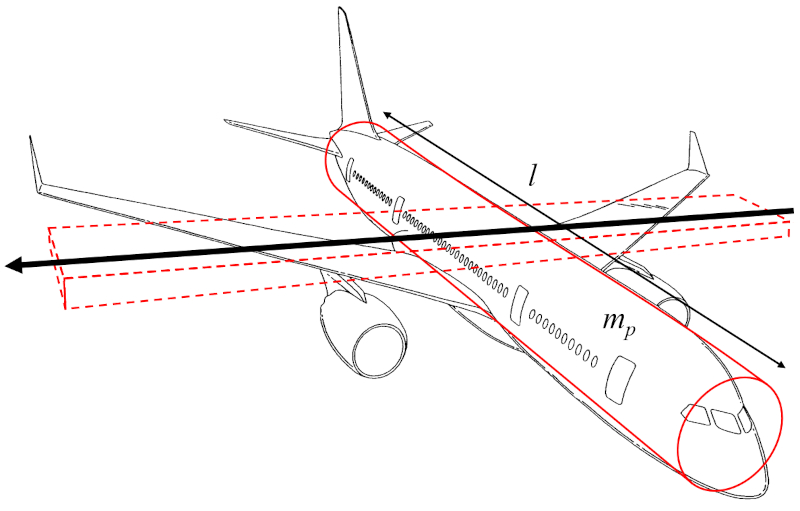
Como o largura da asa ($w$) é muito menor que o distância ao longo da asa ($l$), o termo envolvendo $w^2$ pode ser desprezado, focando apenas em la massa corporal da aeronave ($m_p$) e no termo com o distância ao longo da asa ($l$) ao quadrado.

Portanto, o momento de inércia do eixo da asa ($I_e$) é calculado a partir de la massa corporal da aeronave ($m_p$) e o distância ao longo da asa ($l$), da seguinte maneira:

$I_e = \displaystyle\frac{1}{12} m_p l ^2$

Condições

Variáveis

Relação

ID:(15991, 0)

Top

>Top

Parâmetros

$d_e$

d_e

Centro de distância de massa e elevadores

m

$l$

l

Comprimento do aeronave

m

$c$

c

Constante de proporcionalidade do coeficiente de sustentação

1/rad

$\rho$

rho

Densidade

kg/m^3

$\rho_a$

rho_a

Densidade corporal da aeronave

kg/m^3

$m_p$

m_p

Massa corporal da aeronave

kg

$I_e$

I_e

Momento de inércia do eixo da asa

kg m^2

$S_p$

S_p

Perfil total do objeto

m^2

Variáveis

$\alpha_e$

alpha_e

Aceleração angular do eixo da asa

rad/s^2

$\alpha_s$

alpha_s

Ângulo necessário para elevação

rad

$C_L$

C_L

Coeficiente de elevação

-

$F_L$

F_L

Força de elevação

N

$S_e$

S_e

Superfície do elevador

m^2

$T_e$

T_e

Torque gerado por elevadores

N m

$v$

v

Velocidade em relação ao meio

m/s

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15172, 0)

Equação

>Top, >Modelo

$T_e = d_e F_L$

$T_e = d_e F_e$

Condições

Variáveis

$d_e$

Centro de distância de massa e elevadores

$m$

10215

$F_e$

$F_L$

Força de elevação

$N$

6120

$T_e$

Torque gerado por elevadores

$N m$

10218

Relação

ID:(15163, 0)

Equação

>Top, >Modelo

$T_e = I_e \alpha_e$

Condições

Variáveis

$\alpha_e$

Aceleração angular do eixo da asa

$rad/s^2$

10222

$I_e$

Momento de inércia do eixo da asa

$kg m^2$

10220

$T_e$

Torque gerado por elevadores

$N m$

10218

Relação

ID:(15166, 0)

Equação

>Top, >Modelo

Para gerar uma pressão maior abaixo do que acima da asa e gerar sustentação, utiliza-se o princípio de Bernoulli, corrigindo a falta de conservação da densidade de energia com um coeficiente de elevação ($C_L$). A pressão sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) através da seguinte fórmula:

$F_L =\displaystyle\frac{1}{2} \rho S_e C_L v ^2$

$F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

Condições

Variáveis

$C_L$

Coeficiente de elevação

$-$

6164

$\rho$

Densidade

$kg/m^3$

5342

$F_L$

Força de elevação

$N$

6120

$S_w$

$S_e$

Superfície do elevador

$m^2$

10470

$v$

Velocidade em relação ao meio

$m/s$

6110

Relação

Desenvolvimento

La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em

$F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$

Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),

$S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$

e para o coeficiente de elevação ($C_L$), definido como

$C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$

obtemos

$F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

ID:(4417, 0)

Equação

>Top, >Modelo

A partir de medições, conclui-se que o coeficiente de sustentação $C_L$ é proporcional ao ângulo de ataque $\alpha$:

$C_L = c \alpha$

Condições

Variáveis

$\alpha_s$

Ângulo necessário para elevação

$rad$

6167

$C_L$

Coeficiente de elevação

$-$

6164

$c$

Constante de proporcionalidade do coeficiente de sustentação

$1/rad$

6165

Relação

Após um certo ângulo, a curva diminui até chegar a zero. Isso ocorre porque acima desse ângulo crítico, os redemoinhos cobrem completamente a superfície superior da asa, levando à perda de sustentação. Esse fenômeno é conhecido como \"stall\" (estol em português).

ID:(4441, 0)

Equação

>Top, >Modelo

La massa da asa ($m_w$) é calculado a partir de la massa corporal da aeronave ($m_p$) e ($$)10333

$I_e = \displaystyle\frac{1}{12} m_p l ^2$

Condições

Variáveis

$l$

Comprimento do aeronave

$m$

10469

$m_p$

Massa corporal da aeronave

$kg$

6340

$I_e$

Momento de inércia do eixo da asa

$kg m^2$

10220

Relação

ID:(15987, 0)

Equação

>Top, >Modelo

La massa corporal da aeronave ($m_p$) é calculado a partir de o densidade corporal da aeronave ($\rho_a$), o perfil total do objeto ($S_p$) e o distância ao longo da asa ($l$), da seguinte forma:

$m_p = \rho_a S_p l$

Condições

Variáveis

$l$

Comprimento do aeronave

$m$

10469

$\rho_a$

Densidade corporal da aeronave

$kg/m^3$

6220

$m_p$

Massa corporal da aeronave

$kg$

6340

$S_p$

Perfil total do objeto

$m^2$

6123

Relação

ID:(15985, 0)

Equação

>Top, >Modelo

La centro de distância de massa e elevadores ($d_e$) é definido como a metade de o distância ao longo da asa ($l$), expressado da seguinte maneira:

$d_e = \displaystyle\frac{ l }{2}$

Condições

Variáveis

$d_e$

Centro de distância de massa e elevadores

$m$

10215

$l$

Comprimento do aeronave

$m$

10469

Relação

ID:(15994, 0)