Usuario:
Control de rodar
Storyboard 
El control de alabeo es el mecanismo que permite al avión girar en torno a su eje longitudinal, levantando una de las alas mientras desciende la otra. Este control se logra mediante la generación de una diferencia en la sustentación a través de los alerones, que están ubicados en los extremos de las alas. Esta diferencia de sustentación crea un par de torsión (torque) que provoca el giro del avión alrededor de un eje imaginario a lo largo de su fuselaje, conocido como el eje de alabeo.
ID:(2114, 0)
Control de rodar
Concepto
Para realizar giros en una aeronave, se utilizan los ailerones. Estos generan una una fuerza en los alerones ($F_a$) que, en conjunto con una distancia centro de masa y alerones ($d_a$), inducen una un torque generado por los alerones ($T_a$). Los ailerones se encuentran en las puntas de las alas de la aeronave para maximizar su la distancia centro de masa y alerones ($d_a$) con respecto al centro de masa y lograr una mayor una distancia centro de masa y elevadores ($d_e$).
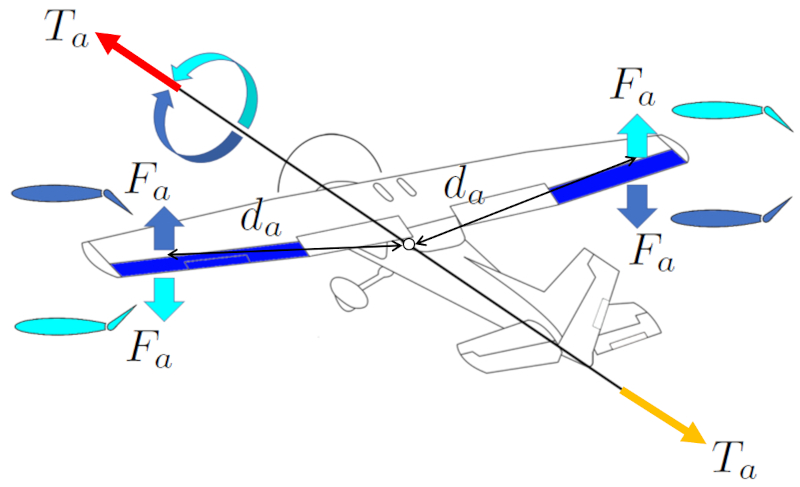
Los ailerones operan de manera asimétrica, lo que significa que si el ailerón del ala derecha genera sustentación hacia arriba, el ailerón del ala izquierda lo hace hacia abajo, y viceversa. De esta forma, estas fuerzas generan un torque que permite girar en sentido horario o antihorario.
El objetivo de la rotación es generar, con la fuerza de sustentación, una fuerza ortogonal al eje central, lo que lleva a una curva en la aeronave. Esto refuerza la acción del timón, ayudando en la maniobra de viraje de la aeronave. De hecho, esta es la forma en que las aves realizan sus maniobras de viraje, ya que no tienen un timón.
Para realizar la maniobra de viraje, el piloto utiliza el control de columna, que tiene un tipo de volante que gira en la misma dirección que la aeronave. En otros casos, como en el joystick de las aeronaves Airbus, no hay un volante, y se inclina el joystick en la dirección deseada para realizar la curva.
Uno de los problemas que surgen al realizar una rotación en torno al eje central de la aeronave es que la fuerza de sustentación se utiliza para desviar la trayectoria, lo que resulta en una disminución de la sustentación. Esto significa que, durante una maniobra de viraje, la aeronave y el ave tienden a perder altura a menos que se incremente la potencia.
ID:(15160, 0)
Aceleración angular de rodar
Concepto
A travez de los alerones se genera una fuerza que induce un torque generado por los alerones ($T_a$). Este a su vez, dependiendo de el momento de inercia eje del avión ($I_a$) genera una aceleración angular eje del avión ($\alpha_a$) que se muestra en la grafica.
Los alerones permiten modificar la inclinación del avión ya sea que esta se genero por ejemplo por vientos curzados o se desea para realizar un viraje. Esto ultimo ocurre pues al ladear el avión la fuerza de sustentación crea una componente lateral que lo desvia.
ID:(11078, 0)
Momento de inercia para rodar
Descripción
El momento de inercia eje del avión ($I_a$) puede aproximarse como el momento de inercia de un paralelepípedo recto que representa el ala de la aeronave, rotando alrededor de un eje paralelo a su ancho:
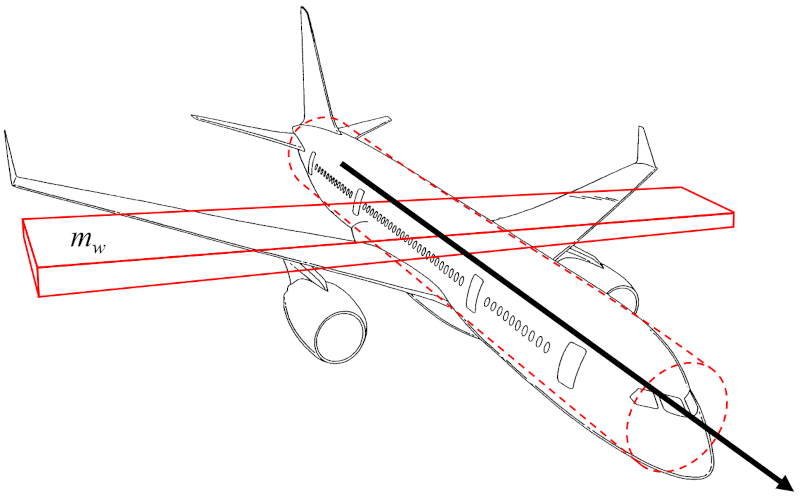
Dado que el cuerpo de la aeronave es relativamente estrecho, se puede, en una primera aproximación, despreciar el momento de inercia del cilindro que lo representa. De esta forma, el momento de inercia eje del avión ($I_a$) resulta proporcional a la masa de las alas ($m_w$) y al cuadrado de la envergadura de las alas ($L$).
Por lo tanto, el momento de inercia eje del avión ($I_a$) se calcula a partir de la masa de las alas ($m_w$) y la envergadura de las alas ($L$), de la siguiente manera:
 $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15992, 0)
Masa de las alas
Descripción
La masa de las alas ($m_w$) se puede aproximar como el volumen de un paralelepípedo recto multiplicado por la densidad de la aeronave:
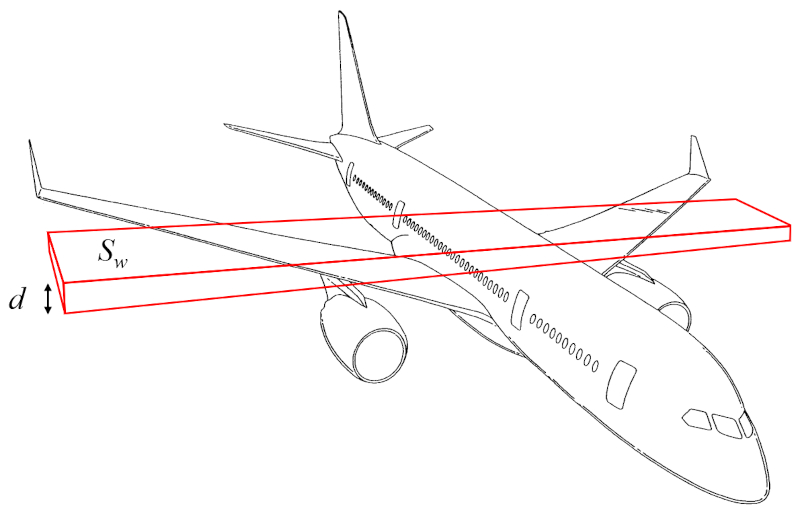
El volumen, por lo tanto, se puede calcular a partir de la superficie que genera sustentación ($S_w$) y la altura del ala ($d$).
Por ello, la masa de las alas ($m_w$) se determina utilizando el densidad del cuerpo de la aeronave ($\rho_a$), la superficie que genera sustentación ($S_w$), y la altura del ala ($d$), de la siguiente manera:
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ C_L = c \alpha $
C_L = c * alpha
$ d_a = \displaystyle\frac{ L }{2}$
d_a = L /2
$ F_L =\displaystyle\frac{1}{2} \rho S_a C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ \gamma_d =\displaystyle\frac{ d }{ L }$
gamma_d = d / L
$ I_a = \displaystyle\frac{1}{6} m_w L ^2$
I_a = m_w * L ^2/6
$ m_w = \rho_a S_w d $
m_w = rho_a * S_w * d
$ T_a = d_a F_L $
T_a = d_a * F_a
$ T_a = I_a \alpha_a $
T_a = I_a * alpha_a
ID:(15974, 0)
Fuerza que genera el rodar
Ecuación
Con los alerones se genera una fuerza en los alerones ($F_a$) que induce via el brazo generado por la distancia centro de masa y alerones ($d_a$) el respectivo el torque generado por los alerones ($T_a$) según:
| $ T_a = d_a F_L $ |
| $ T_a = d_a F_a $ |
ID:(15164, 0)
Torque de rodar
Ecuación
El torque generado por los alerones ($T_a$) se genera la aceleración angular eje del avión ($\alpha_a$) dependiendo de el momento de inercia eje del avión ($I_a$) según:
| $ T_a = I_a \alpha_a $ |
ID:(15167, 0)
Fuerza de sustentación
Ecuación
Para crear una presión mayor debajo que encima del ala y generar sustentación, se emplea la Ley de Bernoulli, corrigiendo la falta de conservación de la densidad de energía mediante un coeficiente de sustentación ($C_L$). La presión sobre el ala, la fuerza de sustentación ($F_L$), se puede estimar utilizando la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) mediante la siguiente fórmula:
| $ F_L =\displaystyle\frac{1}{2} \rho S_a C_L v ^2$ |
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
La fuerza de sustentación ($F_L$), junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$), se encuentra en
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si consideramos la superficie que genera sustentación ($S_w$), definido por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
y para el coeficiente de sustentación ($C_L$), definido como
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
obtenemos
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Constante de sustentación
Ecuación
A partir de mediciones, se concluye que el coeficiente de sustentación ($C_L$) es proporcional al angulo de ataque del ala ($\alpha$) siendo la constante de proporcionalidad del coeficiente de sustentación ($c$):
| $ C_L = c \alpha $ |
Después de cierto ángulo, la curva disminuye hasta llegar a cero. Esto se debe a que sobre dicho ángulo crítico, los vórtices cubren completamente la superficie superior del ala, lo que resulta en la pérdida de sustentación. Este fenómeno se conoce como "stall" (entrada en pérdida).
ID:(4441, 0)
Momento de inercia para rodar
Ecuación
El momento de inercia eje del avión ($I_a$) se calcula a partir de la masa de las alas ($m_w$) y la envergadura de las alas ($L$), de la siguiente manera:
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15986, 0)
Masa de las alas
Ecuación
La masa de las alas ($m_w$) se calcula a partir de el densidad del cuerpo de la aeronave ($\rho_a$), la superficie que genera sustentación ($S_w$) y la altura del ala ($d$), de la siguiente manera:
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Brazo del de la fuerza de los alerones
Ecuación
La distancia centro de masa y alerones ($d_a$) se define como la mitad de la envergadura de las alas ($L$), expresado de la siguiente manera:
| $ d_a = \displaystyle\frac{ L }{2}$ |
ID:(15995, 0)
Relación de espesor a envergadura
Ecuación
El relación de espesor a envergadura ($\gamma_d$) se define como la proporción entre la altura del ala ($d$) y la envergadura de las alas ($L$), expresada de la siguiente forma:
| $ \gamma_d =\displaystyle\frac{ d }{ L }$ |
ID:(15976, 0)