Utilisateur:
Contrôle du roulis
Storyboard 
Le contrôle du roulis est le mécanisme qui permet à l'avion de tourner autour de son axe longitudinal, en levant une aile tandis que l'autre descend. Ce contrôle est obtenu en générant une différence de portance grâce aux ailerons situés aux extrémités des ailes. Cette différence de portance crée un couple responsable de faire pivoter l'avion autour d'un axe imaginaire le long du fuselage, connu sous le nom d'axe de roulis.
ID:(2114, 0)
Contrôle du roulis
Concept
Pour effectuer un roulis autour de son axe, l'aéronef utilise les ailerons. Ils génèrent une une forcer sur les ailerons ($F_a$) qui, combinée à Une distance centre de masse et ailerons ($d_a$), induit une un couple généré par les ailerons ($T_a$). Les ailerons sont situés aux extrémités des ailes de l'aéronef pour maximiser leur a distance centre de masse et ailerons ($d_a$) par rapport au centre de masse et obtenir une plus grande une distance centre de masse et ascenseurs ($d_e$).
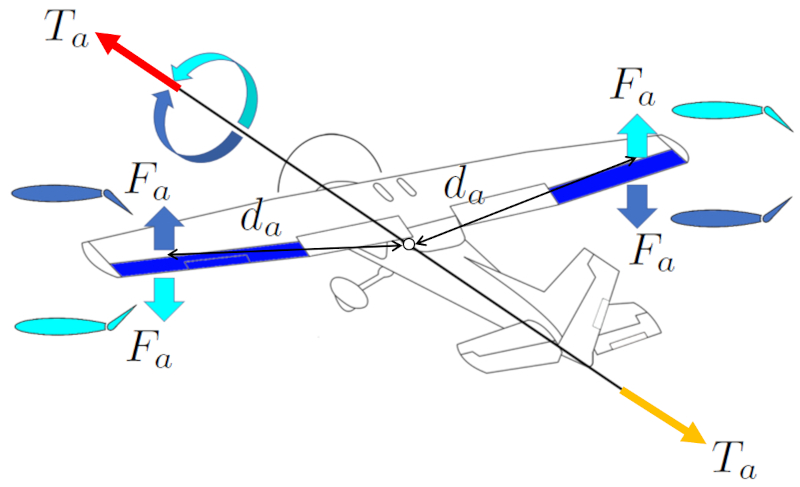
Les ailerons fonctionnent de manière asymétrique, ce qui signifie que si l'aileron de l'aile droite génère une portance vers le haut, celui de l'aile gauche fait le contraire, et vice versa. De cette manière, ces forces génèrent un couple qui permet de tourner dans le sens des aiguilles d'une montre ou dans le sens contraire.
L'objectif de la rotation est de générer, avec la force de portance, une force orthogonale à l'axe central, ce qui entraîne une courbe dans l'aéronef. Cela renforce l'action du gouvernail, aidant ainsi à la manuvre de virage de l'aéronef. En fait, c'est ainsi que les oiseaux réalisent leurs manuvres de virage, car ils ne possèdent pas de gouvernail.
Pour effectuer la manuvre de virage, le pilote utilise le contrôle de colonne, qui comporte un volant qui tourne dans la même direction que l'aéronef. Dans d'autres cas, comme avec le joystick des avions Airbus, il n'y a pas de volant, et le joystick est incliné dans la direction souhaitée pour effectuer la courbe.
Un des problèmes qui surviennent lors de la réalisation d'une rotation autour de l'axe central de l'aéronef est que la force de portance est utilisée pour dévier la trajectoire, ce qui entraîne une diminution de la portance. Cela signifie que, lors d'une manuvre de virage, l'aéronef et l'oiseau ont tendance à perdre de l'altitude à moins que la puissance ne soit augmentée.
ID:(15160, 0)
Moment d'inertie pour rouler
Description
Le moment d'inertie de l'axe de l'avion ($I_a$) peut être approximé comme le moment d'inertie d'un parallélépipède rectangle représentant l'aile de l'avion, tournant autour d'un axe parallèle à sa largeur :
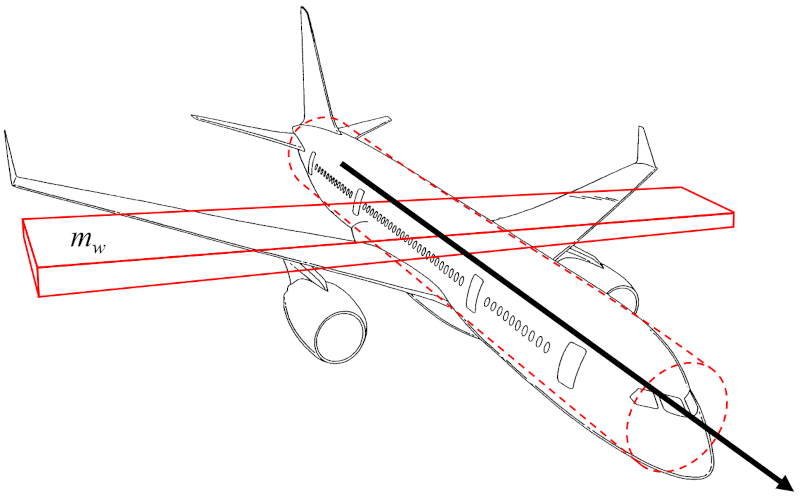
Étant donné que le fuselage de l'avion est relativement étroit, le moment d'inertie du cylindre qui le représente peut être négligé dans une première approximation. Par conséquent, le moment d'inertie de l'axe de l'avion ($I_a$) est proportionnel à A masse de l'aile ($m_w$) et au carré de a envergure des ailes ($L$).
Ainsi, le moment d'inertie de l'axe de l'avion ($I_a$) est calculé à partir de a masse de l'aile ($m_w$) et ($$)6337
 $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15992, 0)
Masse de l'aile
Description
A masse de l'aile ($m_w$) peut être approximé comme le volume d'un parallélépipède rectangle multiplié par la densité de l'aéronef :
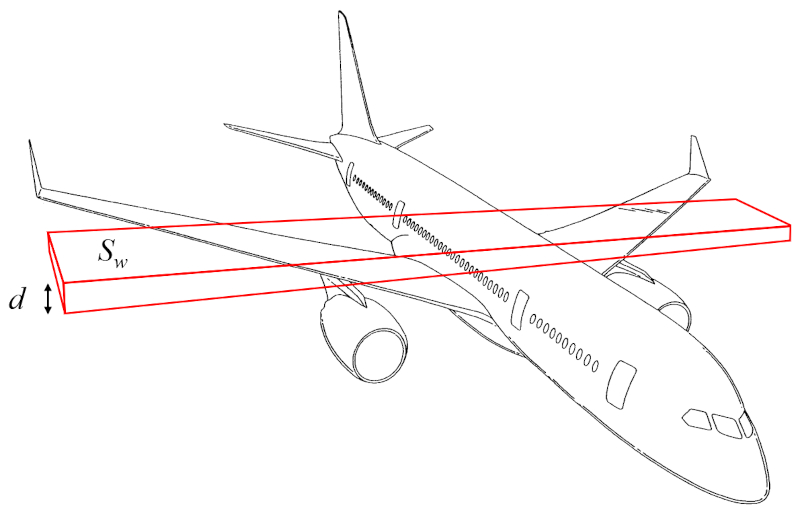
Le volume peut donc être calculé à partir de a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$).
Ainsi, a masse de l'aile ($m_w$) est déterminé en utilisant le densité du corps de l'avion ($\rho_a$), a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$), de la manière suivante :
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Force générée par le roulement
Équation
| $ T_a = d_a F_L $ |
 $ T_a = d_a F_a $ |
ID:(15164, 0)
Couple de roulement
Équation
| $ T_a = I_a \alpha_a $ |
ID:(15167, 0)
Soulevez
Équation
Pour générer une pression plus élevée en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilisé pour corriger le manque de conservation de la densité d'énergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut être estimée en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) grâce à la formule suivante :
| $ F_L =\displaystyle\frac{1}{2} \rho S_a C_L v ^2$ |
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous considérons a surface génératrice de portance ($S_w$), défini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
et pour le coefficient de portance ($C_L$), défini comme
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
nous obtenons
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Constante de levage
Équation
À partir de mesures, il est conclu que le coefficient de portance $C_L$ est proportionnel à l'angle d\'attaque $\alpha$:
| $ C_L = c \alpha $ |
Après un certain angle, la courbe diminue jusqu\'à atteindre zéro. Cela est dû au fait que au-delà de cet angle critique, les tourbillons recouvrent entièrement la surface supérieure de l\'aile, ce qui entraîne une perte de portance. Ce phénomène est appelé \"décrochage\" ou \"décrochage aérodynamique\".
ID:(4441, 0)
Moment d'inertie pour rouler
Équation
Le moment d'inertie de l'axe de l'avion ($I_a$) est calculé à partir de a masse de l'aile ($m_w$) et ($$)6337
| $ I_a = \displaystyle\frac{1}{6} m_w L ^2$ |
ID:(15986, 0)
Masse de l'aile
Équation
A masse de l'aile ($m_w$) est calculé à partir de le densité du corps de l'avion ($\rho_a$), a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$), comme suit :
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Bras de force d'aileron
Équation
A distance centre de masse et ailerons ($d_a$) est défini comme la moitié de a envergure des ailes ($L$), exprimé comme suit :
| $ d_a = \displaystyle\frac{ L }{2}$ |
ID:(15995, 0)
Rapport épaisseur/portée
Équation
Le rapport épaisseur/portée ($\gamma_d$) est défini comme le rapport de a hauteur de l'aile ($d$) à A envergure des ailes ($L$), représenté de la manière suivante :
| $ \gamma_d =\displaystyle\frac{ d }{ L }$ |
ID:(15976, 0)