Utilisateur:
Contrôle du lacet
Storyboard 
Le contrôle de lacet est le mécanisme qui permet à l'avion de pivoter autour de son axe vertical, le dirigeant vers la droite ou vers la gauche. Ce contrôle est obtenu en déviant la gouverne de direction, située à l'arrière de l'avion, au niveau de la queue. En déplaçant la gouverne, une force latérale est générée, créant un couple de torsion qui fait pivoter l'avion autour d'un axe imaginaire perpendiculaire au fuselage, appelé l'axe de lacet.
ID:(2115, 0)
Contrôle du lacet
Concept
Pour effectuer des virages dans une aéronef, on utilise le gouvernail de direction. Il génère une une força no comando ($F_r$), qui, combinée à Une centre de masse et distance du gouvernail ($d_r$), induit une une força no comando ($F_r$). Le gouvernail de direction est situé à l'arrière de l'aéronef pour maximiser une a centre de masse et distance du gouvernail ($d_r$) et obtenir une plus grande une força no comando ($F_r$).
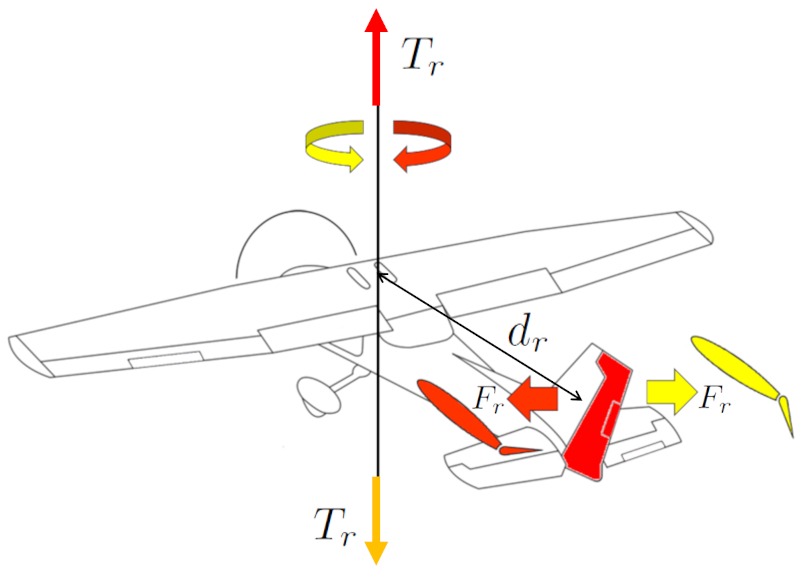
Le pilote contrôle ce mouvement à l'aide des pédales. La direction de la courbe est déterminée par la direction des pédales.
ID:(15162, 0)
Masse de l'aile
Description
A masse de l'aile ($m_w$) peut être approximé comme le volume d'un parallélépipède rectangle multiplié par la densité de l'aéronef :
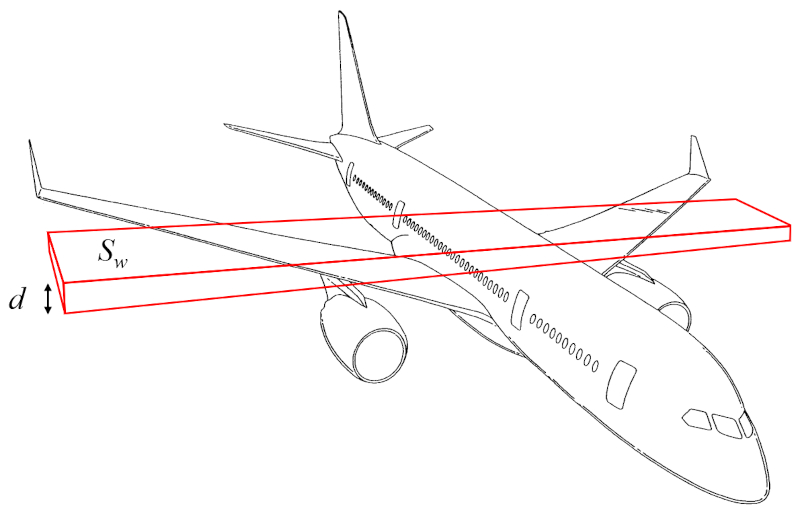
Le volume peut donc être calculé à partir de a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$).
Ainsi, a masse de l'aile ($m_w$) est déterminé en utilisant le densité du corps de l'avion ($\rho_a$), a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$), de la manière suivante :
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Masse corporelle de l'avion
Description
A masse corporelle de l'avion ($m_p$) peut être approximé comme le volume d'un cylindre multiplié par la densité de l'aéronef :
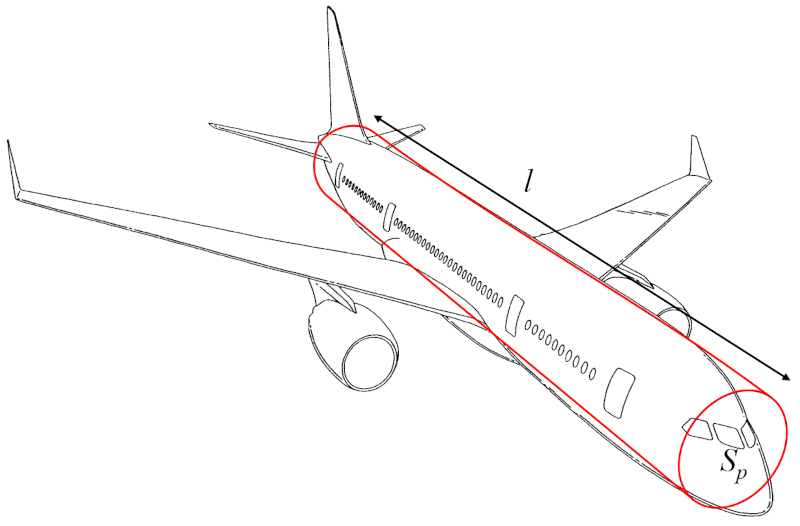
Le volume peut donc être calculé en utilisant le profil total de l'objet ($S_p$) (le rayon ou le diamètre) et le distance le long de l'aile ($l$) (la hauteur du cylindre).
Ainsi, a masse corporelle de l'avion ($m_p$) est déterminé à partir de le densité du corps de l'avion ($\rho_a$), le profil total de l'objet ($S_p$) et le distance le long de l'aile ($l$), de la manière suivante :
| $ m_p = \rho_a S_p l $ |
ID:(15990, 0)
Moment d'inertie pour le lacet
Description
Le moment d'inertie de l'axe vertical ($I_r$) peut être approximé comme la somme du moment d'inertie d'un cylindre représentant le fuselage de l'avion, tournant autour d'un axe perpendiculaire à son axe longitudinal, et du moment d'inertie d'un parallélépipède rectangle représentant les ailes, tournant autour d'un axe perpendiculaire à celles-ci :
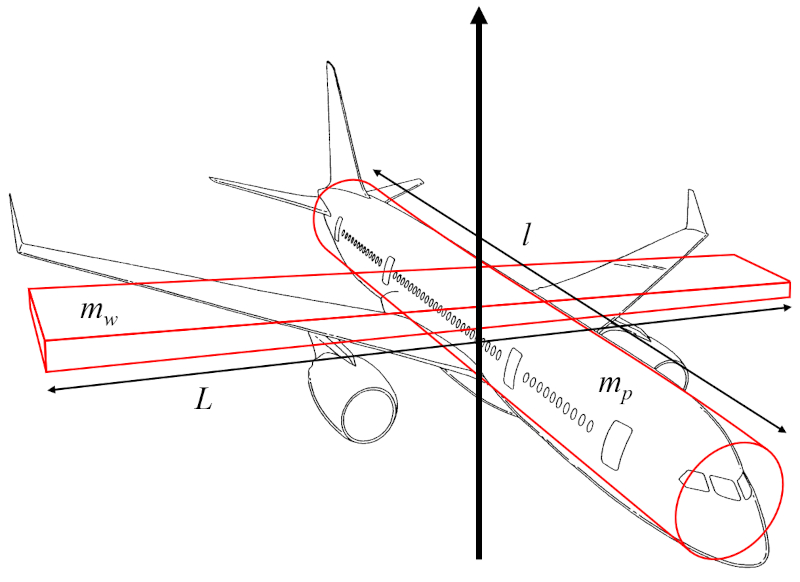
Si, pour l'estimation de le moment d'inertie de l'axe vertical ($I_r$), on suppose que le rayon du cylindre du fuselage est bien inférieur à Le distance le long de l'aile ($l$) et que le largeur de l'aile ($w$) est beaucoup plus petit que a envergure des ailes ($L$), le moment d'inertie du cylindre dépend principalement de a masse corporelle de l'avion ($m_p$) et le distance le long de l'aile ($l$), tandis que le moment d'inertie du parallélépipède dépend de a masse de l'aile ($m_w$) et a envergure des ailes ($L$).
Ainsi, le moment d'inertie de l'axe vertical ($I_r$) est calculé à partir de a masse corporelle de l'avion ($m_p$), a masse de l'aile ($m_w$), ($$)6337 ($$)10333
 $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15993, 0)
Force qui génère le lacet
Équation
| $ T_r = d_r F_L $ |
 $ T_r = d_r F_r $ |
ID:(15165, 0)
Couple de lacet
Équation
| $ T_r = I_r \alpha_r $ |
ID:(15168, 0)
Soulevez
Équation
Pour générer une pression plus élevée en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilisé pour corriger le manque de conservation de la densité d'énergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut être estimée en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) grâce à la formule suivante :
| $ F_L =\displaystyle\frac{1}{2} \rho S_r C_L v ^2$ |
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous considérons a surface génératrice de portance ($S_w$), défini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
et pour le coefficient de portance ($C_L$), défini comme
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
nous obtenons
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Constante de levage
Équation
À partir de mesures, il est conclu que le coefficient de portance $C_L$ est proportionnel à l'angle d\'attaque $\alpha$:
| $ C_L = c \alpha $ |
Après un certain angle, la courbe diminue jusqu\'à atteindre zéro. Cela est dû au fait que au-delà de cet angle critique, les tourbillons recouvrent entièrement la surface supérieure de l\'aile, ce qui entraîne une perte de portance. Ce phénomène est appelé \"décrochage\" ou \"décrochage aérodynamique\".
ID:(4441, 0)
Moment d'inertie pour le lacet
Équation
Le moment d'inertie de l'axe vertical ($I_r$) est calculé à partir de a masse de l'aile ($m_w$), a envergure des ailes ($L$) et ($$)10333
| $ I_r = \displaystyle\frac{1}{12}( m_p l ^2 + m_w L ^2)$ |
ID:(15988, 0)
Masse de l'aile
Équation
A masse de l'aile ($m_w$) est calculé à partir de le densité du corps de l'avion ($\rho_a$), a surface génératrice de portance ($S_w$) et a hauteur de l'aile ($d$), comme suit :
| $ m_w = \rho_a S_w d $ |
ID:(15984, 0)
Masse corporelle de l'avion
Équation
A masse corporelle de l'avion ($m_p$) est calculé à partir de le densité du corps de l'avion ($\rho_a$), le profil total de l'objet ($S_p$) et le distance le long de l'aile ($l$), comme suit :
| $ m_p = \rho_a S_p l $ |
ID:(15985, 0)
Bras de force de gouvernail
Équation
A centre de masse et distance du gouvernail ($d_r$) est défini comme la moitié de le distance le long de l'aile ($l$), exprimé comme suit :
| $ d_r = \displaystyle\frac{ l }{2}$ |
ID:(15996, 0)
Rapport épaisseur/portée
Équation
Le rapport épaisseur/portée ($\gamma_d$) est défini comme le rapport de a hauteur de l'aile ($d$) à A envergure des ailes ($L$), représenté de la manière suivante :
| $ \gamma_d =\displaystyle\frac{ d }{ L }$ |
ID:(15976, 0)