Storyboard

Pitch control is the mechanism that allows the aircraft's nose to be raised or lowered, which is essential for ascending or descending movement. This control is achieved by generating lift through the elevators located on the smaller wings near the tail of the aircraft. This lift creates a torque, responsible for causing the aircraft to rotate around an imaginary axis, parallel to the main wings, known as the pitch axis.

>Model

ID:(2113, 0)

Iframe

>Top

ID:(15171, 0)

Concept

>Top

To pitch the aircraft's nose up or down, the elevators are used. Both elevators are employed in a symmetrical manner to generate a the force in the elevators ($F_e$) symmetric effect. Placing them at the tail of the aircraft achieves ($$) greater effectiveness by locating them near the center of mass. This provides sufficient control to raise or lower the aircraft's nose.

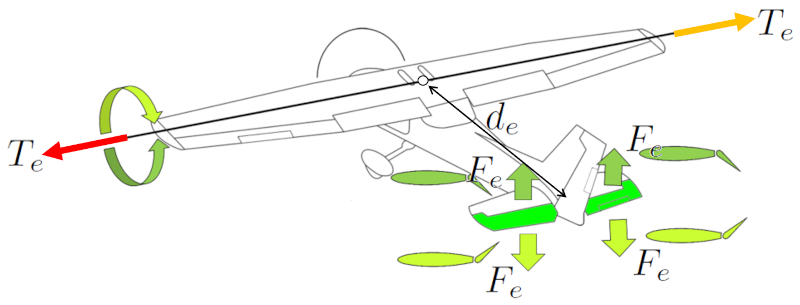
In older aircraft, control of the rear ailerons is achieved through a control stick, where pushing forward causes the aircraft's nose to descend, and pulling backward raises the nose. In Airbus family aircraft, this control is accomplished using a joystick.

In the case of birds, a similar solution exists, although in this case, the tail is not interrupted by a rudder.

ID:(15161, 0)

Concept

>Top

ID:(11079, 0)

Description

>Top

The wing mass ($m_w$) can be approximated as the volume of a rectangular parallelepiped multiplied by the density of the aircraft:

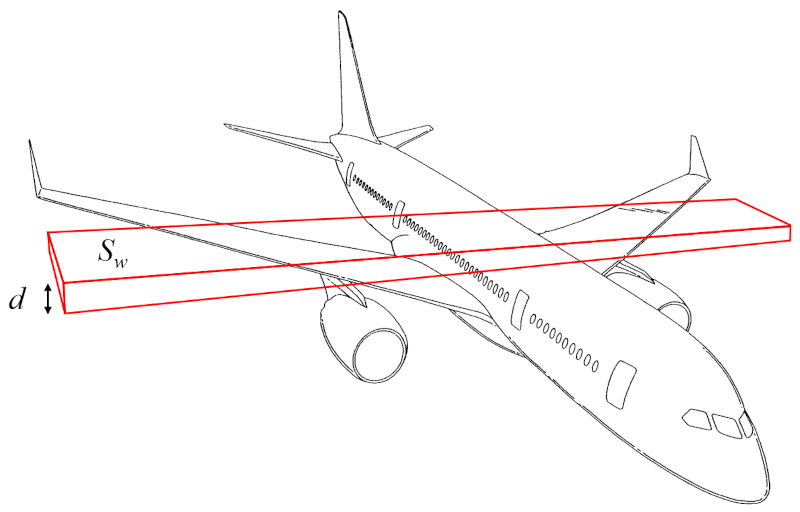
The volume can thus be calculated from the surface that generates lift ($S_w$) and the wing height ($d$).

Therefore, the wing mass ($m_w$) is determined using the aircraft body density ($\rho_a$), the surface that generates lift ($S_w$), and the wing height ($d$), as follows:

ID:(15989, 0)

Description

>Top

The wing axis moment of inertia ($I_e$) can be approximated as the moment of inertia of a cylinder representing the body of the aircraft, rotating around an axis perpendicular to the cylinder's axis, which is parallel to the wings:

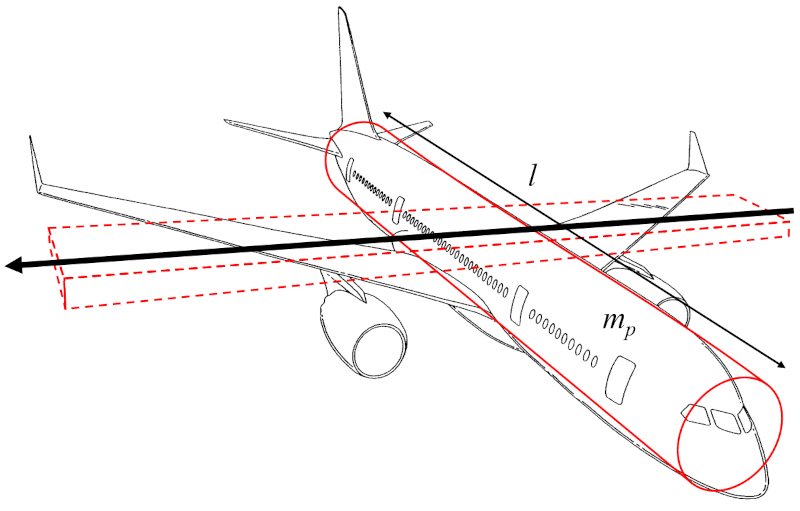
Since the wing width ($w$) is much smaller than the distance along the wing ($l$), the term involving $w^2$ can be neglected, focusing only on the aircraft body mass ($m_p$) and the term with the distance along the wing ($l$) squared.

Therefore, the wing axis moment of inertia ($I_e$) is calculated using the aircraft body mass ($m_p$) and the distance along the wing ($l$) as follows:

$I_e = \displaystyle\frac{1}{12} m_p l ^2$

Conditions

Variables

Relation

ID:(15991, 0)

Top

>Top

Parameters

$\rho_a$

rho_a

Aircraft body density

kg/m^3

$m_p$

m_p

Aircraft body mass

kg

$l$

l

Aircraft length

m

$\rho$

rho

Density

kg/m^3

$d_e$

d_e

Distance center of mass and elevators

m

$c$

c

Proportionality constant coefficient sustainability

1/rad

$S_p$

S_p

Total object profile

m^2

$I_e$

I_e

Wing axis moment of inertia

kg m^2

Variables

$\alpha_s$

alpha_s

Angle required for lift

rad

$S_e$

S_e

Elevator surface

m^2

$F_L$

F_L

Lift force

N

$C_L$

C_L

Simple Model for Sustainability Coefficient

-

$v$

v

Speed with respect to the medium

m/s

$T_e$

T_e

Torque generated by elevators

N m

$\alpha_e$

alpha_e

Wing axis angular acceleration

rad/s^2

Calculations

• Alternative method
• Traditional method
• Strategy
• 2D
• 3D

Equation

Number

First, select the equation: to , then, select the variable: to

---

Calculations

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable Given Calculate Target : Equation To be used

Equations

ID:(15172, 0)

Equation

>Top, >Model

$T_e = d_e F_L$

$T_e = d_e F_e$

Conditions

Variables

$d_e$

Distance center of mass and elevators

$m$

10215

$F_e$

$F_L$

Lift force

$N$

6120

$T_e$

Torque generated by elevators

$N m$

10218

Relation

ID:(15163, 0)

Equation

>Top, >Model

$T_e = I_e \alpha_e$

Conditions

Variables

$T_e$

Torque generated by elevators

$N m$

10218

$\alpha_e$

Wing axis angular acceleration

$rad/s^2$

10222

$I_e$

Wing axis moment of inertia

$kg m^2$

10220

Relation

ID:(15166, 0)

Equation

>Top, >Model

To generate higher pressure below than above the wing and generate lift, Bernoulli's principle is employed, correcting for the lack of energy density conservation using ($$). The pressure over the wing, the lift force ($F_L$), can be estimated using the density ($\rho$), the surface that generates lift ($S_w$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) through the following formula:

$F_L =\displaystyle\frac{1}{2} \rho S_e C_L v ^2$

$F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

Conditions

Variables

$\rho$

Density

$kg/m^3$

5342

$F_L$

Lift force

$N$

6120

$C_L$

Simple Model for Sustainability Coefficient

$-$

6164

$v$

Speed with respect to the medium

$m/s$

6110

$S_w$

$S_e$

Elevator surface

$m^2$

10470

Relation

Development

The lift force ($F_L$), along with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$), is found in

$F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$

If we consider the surface that generates lift ($S_w$), given by the wing span ($L$), the upper wing length ($l_t$), and the bottom wing length ($l_b$),

$S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$

and for the coefficient of lift ($C_L$), defined as

$C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$

we obtain

$F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

ID:(4417, 0)

Equation

>Top, >Model

From measurements, it is concluded that the lift coefficient $C_L$ is proportional to the angle of attack $\alpha$:

$C_L = c \alpha$

Conditions

Variables

$\alpha_s$

Angle required for lift

$rad$

6167

$c$

Proportionality constant coefficient sustainability

$1/rad$

6165

$C_L$

Simple Model for Sustainability Coefficient

$-$

6164

Relation

After a certain angle, the curve decreases until it reaches zero. This is because beyond that critical angle, the vortices fully cover the upper surface of the wing, leading to a loss of lift. This phenomenon is known as \"stall\".

ID:(4441, 0)

Equation

>Top, >Model

The wing mass ($m_w$) is calculated from the aircraft body mass ($m_p$) and the distance along the wing ($l$), as follows:

$I_e = \displaystyle\frac{1}{12} m_p l ^2$

Conditions

Variables

$m_p$

Aircraft body mass

$kg$

6340

$l$

Aircraft length

$m$

10469

$I_e$

Wing axis moment of inertia

$kg m^2$

10220

Relation

ID:(15987, 0)

Equation

>Top, >Model

The aircraft body mass ($m_p$) is calculated from the aircraft body density ($\rho_a$), the total object profile ($S_p$), and the distance along the wing ($l$), as follows:

$m_p = \rho_a S_p l$

Conditions

Variables

$\rho_a$

Aircraft body density

$kg/m^3$

6220

$m_p$

Aircraft body mass

$kg$

6340

$l$

Aircraft length

$m$

10469

$S_p$

Total object profile

$m^2$

6123

Relation

ID:(15985, 0)

Equation

>Top, >Model

The distance center of mass and elevators ($d_e$) is defined as half of the distance along the wing ($l$), expressed as follows:

$d_e = \displaystyle\frac{ l }{2}$

Conditions

Variables

$l$

Aircraft length

$m$

10469

$d_e$

Distance center of mass and elevators

$m$

10215

Relation

ID:(15994, 0)