Benützer:
Pitch-Kontrolle
Storyboard 
Die Höhensteuerung (Pitch Control) ist der Mechanismus, der es ermöglicht, die Nase des Flugzeugs zu heben oder zu senken, was entscheidend für den Auf- oder Abstieg der Maschine ist. Diese Steuerung wird durch die Erzeugung von Auftrieb mithilfe der Höhenruder erreicht, die sich an den kleineren Flügeln in der Nähe des Hecks des Flugzeugs befinden. Dieser Auftrieb erzeugt ein Drehmoment, das das Flugzeug um eine imaginäre Achse, parallel zu den Hauptflügeln, dreht, die als Nickachse (Pitch Axis) bezeichnet wird.
ID:(2113, 0)
Pitch-Kontrolle
Konzept
Um die Nase des Flugzeugs nach oben oder unten zu neigen, werden die Höhenruder verwendet. Beide Höhenruder werden symmetrisch eingesetzt, um eine die Kraft auf den Auftriebselementen ($F_e$) symmetrische Wirkung zu erzeugen. Indem sie am Heck des Flugzeugs platziert werden, wird eine ($$) größere Effektivität erzielt, da sie sich in der Nähe des Schwerpunkts befinden. Dies ermöglicht ausreichende Kontrolle, um die Nase des Flugzeugs anzuheben oder abzusenken.
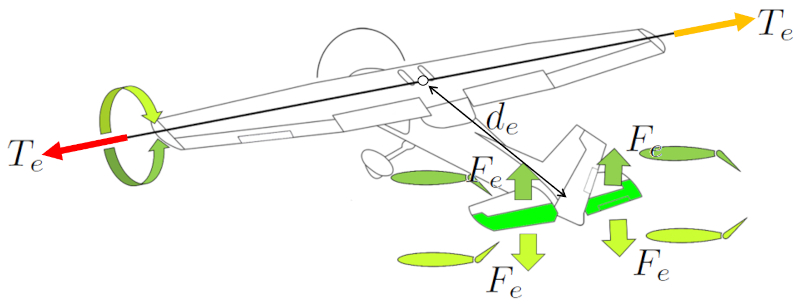
Bei älteren Flugzeugen erfolgt die Steuerung der hinteren Querruder über einen Steuerknüppel, bei dem das Drücken nach vorne dazu führt, dass die Nase des Flugzeugs sinkt, während das Ziehen nach hinten die Nase anhebt. Bei Flugzeugen der Airbus-Familie erfolgt diese Steuerung über einen Joystick.
Im Falle von Vögeln gibt es eine ähnliche Lösung, wobei der Schwanz jedoch nicht durch ein Seitenruder unterbrochen ist.
ID:(15161, 0)
Flügelmasse
Beschreibung
Die Flügelmasse ($m_w$) kann als das Volumen eines rechtwinkligen Parallelepipeds multipliziert mit der Dichte des Flugzeugs approximiert werden:
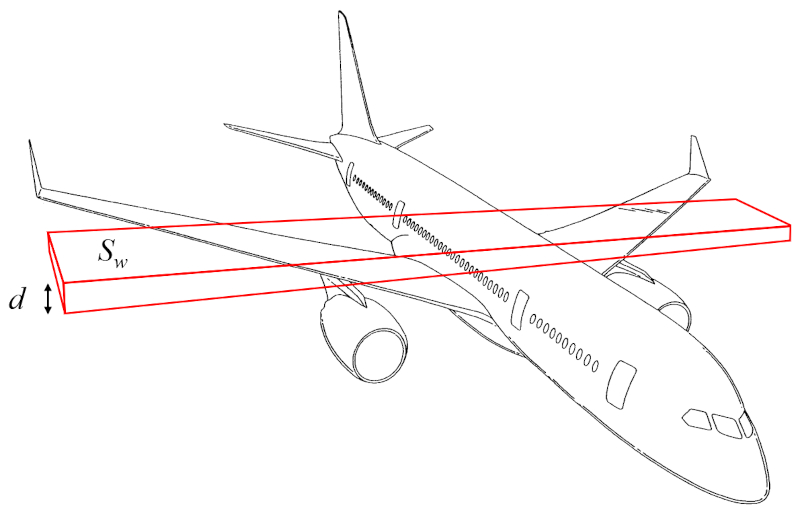
Das Volumen kann somit aus die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Flügelhöhe ($d$) berechnet werden.
Daher wird die Flügelmasse ($m_w$) unter Verwendung von der Dichte des Flugzeugkörpers ($\rho_a$), die Oberfläche, die Auftrieb erzeugt ($S_w$) und die Flügelhöhe ($d$) wie folgt bestimmt:
| $ m_w = \rho_a S_w d $ |
ID:(15989, 0)
Trägheitsmoment beim Nicken
Beschreibung
Der Trägheitsmoment der Flügelachse ($I_e$) kann als das Trägheitsmoment eines Zylinders approximiert werden, der den Rumpf des Flugzeugs darstellt und sich um eine Achse dreht, die senkrecht zur Achse des Zylinders und parallel zu den Flügeln verläuft:
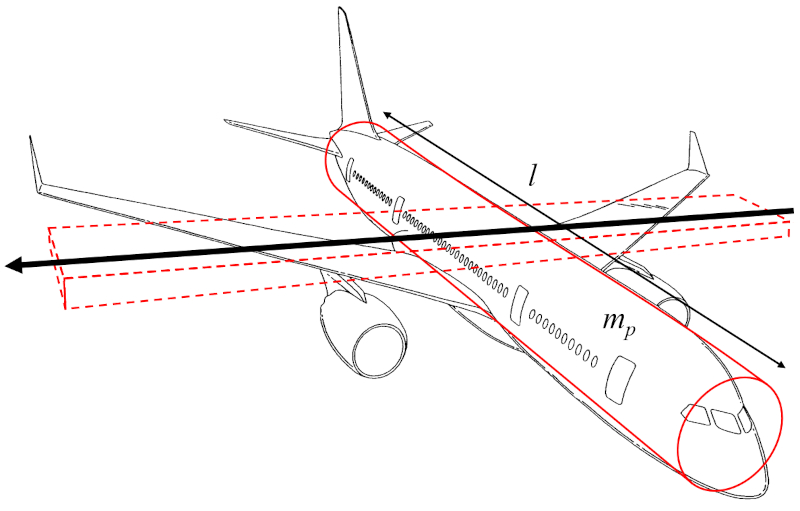
Da der Flügelbreite ($w$) deutlich kleiner ist als der Abstand entlang des Flügels ($l$), kann der Term mit $w^2$ vernachlässigt werden, und es wird nur mit die Flugzeugkörpermasse ($m_p$) und dem Quadrat von der Abstand entlang des Flügels ($l$) gearbeitet.
Daher wird der Trägheitsmoment der Flügelachse ($I_e$) wie folgt aus die Flugzeugkörpermasse ($m_p$) und der Abstand entlang des Flügels ($l$) berechnet:
 $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15991, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ C_L = c \alpha $
C_L = c * alpha
$ d_e = \displaystyle\frac{ l }{2}$
d_e = l /2
$ F_L =\displaystyle\frac{1}{2} \rho S_e C_L v ^2$
F_L = rho * S_w * C_L * v ^2/2
$ I_e = \displaystyle\frac{1}{12} m_p l ^2$
I_e = m_p * l ^2/12
$ m_p = \rho_a S_p l $
m_p = rha_a * S_p * l
$ T_e = d_e F_L $
T_e = d_e * F_e
$ T_e = I_e \alpha_e $
T_e = I_e * alpha_e
ID:(15172, 0)
Durch das Nicken erzeugte Kraft
Gleichung
| $ T_e = d_e F_L $ |
| $ T_e = d_e F_e $ |
ID:(15163, 0)
Pitch-Drehmoment
Gleichung
| $ T_e = I_e \alpha_e $ |
ID:(15166, 0)
Auftriebskraft
Gleichung
Um einen höheren Druck unterhalb als oberhalb des Flügels zu erzeugen und Auftrieb zu generieren, wird das Bernoulli-Prinzip angewendet und die fehlende Energieerhaltungsdichte durch ein Koeffizient Fahrstuhl ($C_L$) korrigiert. Der Druck über dem Flügel, die Auftriebskraft ($F_L$), kann unter Verwendung von die Dichte ($\rho$), die Oberfläche, die Auftrieb erzeugt ($S_w$), der Koeffizient Fahrstuhl ($C_L$) und die Geschwindigkeit in Bezug auf das Medium ($v$) mithilfe der folgenden Formel geschätzt werden:
| $ F_L =\displaystyle\frac{1}{2} \rho S_e C_L v ^2$ |
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
Die Auftriebskraft ($F_L$), zusammen mit die Spannweite der Flügel ($L$), die Dichte ($\rho$), der Flügel-Höchstgeschwindigkeitsfaktor ($c_t$), der Flügelbodengeschwindigkeitsfaktor ($c_b$), die Obere Flügellänge ($l_t$), die Länge des unteren Flügels ($l_b$) und die Geschwindigkeit in Bezug auf das Medium ($v$), findet sich in
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Wenn wir die Oberfläche, die Auftrieb erzeugt ($S_w$) betrachten, gegeben durch die Spannweite der Flügel ($L$), die Obere Flügellänge ($l_t$) und die Länge des unteren Flügels ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
und für der Koeffizient Fahrstuhl ($C_L$), definiert als
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
erhalten wir
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Auftriebsbeiwert
Gleichung
Aus Messungen geht hervor, dass der Auftriebskoeffizient $C_L$ proportional zum Anstellwinkel $\alpha$ ist:
| $ C_L = c \alpha $ |
Nach einem bestimmten Winkel nimmt die Kurve ab und erreicht schließlich den Wert Null. Dies liegt daran, dass über diesem kritischen Winkel die Wirbel vollständig die obere Fläche des Flügels bedecken und somit der Auftrieb verloren geht. Dieses Phänomen wird als \"Strömungsabriss\" bezeichnet.
ID:(4441, 0)
Trägheitsmoment beim Nicken
Gleichung
Die Flügelmasse ($m_w$) wird aus die Flugzeugkörpermasse ($m_p$) und der Abstand entlang des Flügels ($l$) berechnet, wie folgt:
| $ I_e = \displaystyle\frac{1}{12} m_p l ^2$ |
ID:(15987, 0)
Flugzeugkörpermasse
Gleichung
Die Flugzeugkörpermasse ($m_p$) wird aus der Dichte des Flugzeugkörpers ($\rho_a$), der Gesamtobjektprofil ($S_p$) und der Abstand entlang des Flügels ($l$) berechnet, wie folgt:
| $ m_p = \rho_a S_p l $ |
ID:(15985, 0)
Nickkraftarm
Gleichung
Die Entfernung Schwerpunkt und Aufzüge ($d_e$) wird als die Hälfte von der Abstand entlang des Flügels ($l$) definiert, dargestellt wie folgt:
| $ d_e = \displaystyle\frac{ l }{2}$ |
ID:(15994, 0)