Cellular Automata
Definición 
Los autómatas celulares son modelos en que discretiza el espacio tiempo y se definen autómatas en cada punto (célula) de la red que actúan en función de lo que hacen sus vecinos (autómatas pues tienen una forma definida de reaccionar). Un ejemplo es una estructura hexagonal:
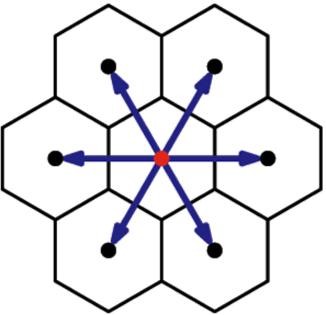
Modelo D2Q7 (dos dimensiones y 7 elementos por celda - 6 lados y 1 centro)
En el caso que se aplica a un gas de partículas, cada nodo puede o no contener (estados 0 y 1) una partícula que puede solo tener las velocidades con las direcciones que los links entre celdas.
En la simulación con modelos tipo autómatas celulares existen dos fases:
- celda actúa sobre las demás
- celda procesa actuaciones del entorno
En el caso especial de que se modela un gas el primer paso corresponde al flujo (streaming) mientras que el segundo a las colisiones (collision).
la descripción matemática se realiza mediante la función de distribución de partículas
| $f_i(\vec{x},t)=w_if(\vec{x},\vec{v}_i,t)$ |
ID:(8494, 0)
Simulador con camino discreto
Imagen 
En este caso se considera un sistema en que la partícula inicia su viaje siempre en el origen en dirección del eje positivo. El espacio al lado izquierdo del borde definido en 'Border' tiene una probabilidad de colisión
Uno puede experimentar eligiendo por ejemplo un medio B 'duro' es decir con una probabilidad alta (
ID:(9103, 0)
Modelos D2Q9 (2 dimensiones, 9 puntos)
Nota 
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n
$\vec{e}_0=(0,0)$
\\n\\nen las esquinas\\n\\n
$\vec{e}_1=(1,0)$
(E),\\n
$\vec{e}_2=(0,1)$
(N), \\n
$\vec{e}_3=(-1,0)$
(W) y \\n
$\vec{e}_4=(0,-1)$
(S)\\n\\ny en las diagonales\\n\\n
$\vec{e}_5=(1,1)$
(NE), \\n
$\vec{e}_6=(-1,1)$
(SE), \\n
$\vec{e}_7=(-1,-1)$
(SW) y \\n
$\vec{e}_8=(1,-1)$
(NW)
lo que se representa en la siguiente gráfica:
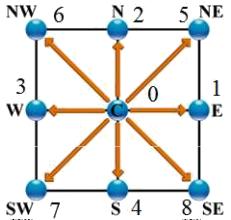
ID:(8496, 0)
Modelos D3Q15 (3 dimensiones, 15 puntos)
Cita 
El modelo D3Q15 es un modelo bidimensional (D3) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\n
$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) y (0,0,-1)$
\\n\\ny en las esquinas del cubo\\n\\n
$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$
lo que se representa en la siguiente gráfica:
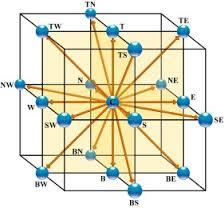
Es facil que se pueden construir modelos del tipo D3Q19 (incluyendo las mitades de las aristas laterales) o D3Q27 (todos los puntos posibles).
ID:(8497, 0)
Discretización y Estructura de Celdas del Enfoque LBM
Descripción 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Los aut matas celulares son modelos en que discretiza el espacio tiempo y se definen aut matas en cada punto (c lula) de la red que act an en funci n de lo que hacen sus vecinos (aut matas pues tienen una forma definida de reaccionar). Un ejemplo es una estructura hexagonal:

Modelo D2Q7 (dos dimensiones y 7 elementos por celda - 6 lados y 1 centro)
En el caso que se aplica a un gas de part culas, cada nodo puede o no contener (estados 0 y 1) una part cula que puede solo tener las velocidades con las direcciones que los links entre celdas.
En la simulaci n con modelos tipo aut matas celulares existen dos fases:
- celda act a sobre las dem s
- celda procesa actuaciones del entorno
En el caso especial de que se modela un gas el primer paso corresponde al flujo (streaming) mientras que el segundo a las colisiones (collision).
la descripci n matem tica se realiza mediante la funci n de distribuci n de part culas
| $f_i(\vec{x},t)=w_if(\vec{x},\vec{v}_i,t)$ |
(ID 8494)
La dispersi n se asocia al tiempo de relajaci n
| $\eta=\displaystyle\frac{\rho(2\tau -1)}{6}\displaystyle\frac{\Delta x^2}{\Delta t}$ |
con
(ID 9158)
En el caso de la discretizaci n en los modelos LBM se trabaja no con funciones de la velocidad si no que con componentes discretas. De esta forma se define la componente
| $f_i(\vec{x},t)=w_if(\vec{x},\vec{v}_i,t)$ |
en donde
(ID 8466)
En este caso se considera un sistema en que la part cula inicia su viaje siempre en el origen en direcci n del eje positivo. El espacio al lado izquierdo del borde definido en 'Border' tiene una probabilidad de colisi n
Uno puede experimentar eligiendo por ejemplo un medio B 'duro' es decir con una probabilidad alta (
(ID 9103)
Al discretizar asumimos que las part culas se mueven con una velocidad media
| $ c =\displaystyle\frac{ \Delta x }{ \Delta t }$ |
(ID 9157)
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n
$\vec{e}_0=(0,0)$
\\n\\nen las esquinas\\n\\n
$\vec{e}_1=(1,0)$
(E),\\n
$\vec{e}_2=(0,1)$
(N), \\n
$\vec{e}_3=(-1,0)$
(W) y \\n
$\vec{e}_4=(0,-1)$
(S)\\n\\ny en las diagonales\\n\\n
$\vec{e}_5=(1,1)$
(NE), \\n
$\vec{e}_6=(-1,1)$
(SE), \\n
$\vec{e}_7=(-1,-1)$
(SW) y \\n
$\vec{e}_8=(1,-1)$
(NW)
lo que se representa en la siguiente gr fica:

(ID 8496)
El modelo D3Q15 es un modelo bidimensional (D3) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\n
$(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) y (0,0,-1)$
\\n\\ny en las esquinas del cubo\\n\\n
$(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)$
lo que se representa en la siguiente gr fica:

Es facil que se pueden construir modelos del tipo D3Q19 (incluyendo las mitades de las aristas laterales) o D3Q27 (todos los puntos posibles).
(ID 8497)
ID:(1135, 0)
