Inertie
Storyboard 
Si aucune force externe n'agit sur un objet, celui-ci aura tendance à maintenir son état actuel, ce qui signifie que sa vitesse reste constante.
Ce phénomène est connu sous le nom d'inertie et donne lieu au premier principe de Newton, qui généralise cette idée en affirmant que les objets ont tendance à maintenir leur moment constant, ce qui, dans le cas d'une masse constante, se réduit à une vitesse constante.
ID:(754, 0)
Crayon comme projectile
Citation 
Si un crayon graphite est tiré d\'un canon à haute vitesse, il se comporte comme s\'il était hautement rigide et peut pénétrer des planches de bois sans être endommagé

ID:(2882, 0)
Pailles comme projectiles
Exercer 
Si une simple paille est tirée d\'un canon à haute vitesse, elle devient si rigide qu\'elle peut pénétrer des objets comme une pomme de terre sans être endommagée ni pliée:

ID:(2883, 0)
Retirer la nappe sans déplacer la vaisselle
Équation 
Si la nappe est retirée suffisamment rapidement sous la vaisselle, par inertie, la vaisselle restera en place et retombera simplement sur la table une fois la nappe retirée. Si le processus est effectué lentement, la vaisselle suivra la nappe et finira par tomber sur le sol.

ID:(2881, 0)
Manière de jouer Jenga
Script 
Tout joueur de Jenga qui réussit sait que la seule façon d\'éviter que la tour ne tombe est de retirer les blocs avec de petits coups rapides qui enlèvent les éléments rapidement, plutôt que de les déplacer lentement. La raison en est que le mouvement lent des blocs rend la tour instable et peut éventuellement la faire tomber. Cependant, si le mouvement est effectué rapidement, grâce à l\'inertie, la tour reste debout et quand elle commence à réagir, elle est déjà dans une position stable.

ID:(2880, 0)
Space Shuttle
Variable 
La navette spatiale était un programme de la NASA conçu pour permettre à un vaisseau spatial d\'atteindre l\'orbite, de réaliser des opérations telles que le déploiement, la réparation ou la récupération d\'un satellite, et de retourner sur la surface de la Terre. Au cours du processus, seul le réservoir principal de carburant était perdu, les deux propulseurs montés sur ses côtés étant récupérés via un parachute après une chute. Le réservoir était isolé avec une couche protectrice, car le carburant devait être maintenu à basse température.

L\'un des accidents mortels du programme des navettes spatiales s\'est produit lorsqu\'un morceau d\'isolation du réservoir principal de carburant s\'est détaché lors du décollage. Le morceau, de la taille d\'une brique, avait la consistance de mousse de plastique, mais en raison de la grande vitesse à laquelle il se déplaçait, son inertie l\'a transformé en un objet rigide. En conséquence, lorsqu\'il a heurté l\'aile de la navette spatiale, il a créé un trou plusieurs fois plus grand que l\'objet lui-même. Ce dommage est passé inaperçu, et lorsque la navette est revenue dans l\'atmosphère une semaine plus tard, les gaz incandescents créés par la friction avec l\'atmosphère ont causé la désintégration de l\'aile. Cela a rendu la navette incontrôlable et elle s\'est écrasée.

ID:(13999, 0)
Inertie
Description 
Si aucune force externe n'agit sur un objet, celui-ci aura tendance à maintenir son état actuel, ce qui signifie que sa vitesse reste constante. Ce phénomène est connu sous le nom d'inertie et donne lieu au premier principe de Newton, qui généralise cette idée en affirmant que les objets ont tendance à maintenir leur moment constant, ce qui, dans le cas d'une masse constante, se réduit à une vitesse constante.
Variables
Calculs
Calculs
Équations
(ID 4355)
(ID 10283)
(ID 10283)
(ID 15538)
Exemples
(ID 15472)
Tout objet a une inertie, ce qui signifie qu\'il r siste aux changements de son tat. L\' tat est associ la vitesse qu\'il poss de, tandis que l\'inertie elle-m me est associ e la fois la vitesse et la masse inertielle appel e. Bien que la masse co ncide avec la valeur d termin e par une balance (masse gravitationnelle), sa signification physique est diff rente car l\'inertie se produit m me dans des situations o il n\'y a pas de gravit .
Pour d terminer sa valeur, il faut mesurer la quantit de force qui acc l re un corps. Cependant, il est courant de supposer la valeur en mesurant simplement la masse gravitationnelle, car elle co ncide avec la valeur de la masse inertielle.
La mesure de la masse inertielle, tout comme la masse gravitationnelle, est exprim e en kilogrammes (syst me MKS).
(ID 2879)
L'inertie fait r f rence la tendance des corps maintenir leur tat actuel. Autrement dit, une force est n cessaire pour modifier leur vitesse. Si la force appliqu e est tr s faible, elle n'aura aucun effet sur les corps. Par exemple, sur une table recouverte d'une nappe glissante, la nappe peut tre rapidement retir e sans que la vaisselle ne bouge.
Une des cons quences de l'inertie est que chaque corps maintiendra son tat, que ce soit au repos ou en mouvement uniforme dans une ligne droite, moins d' tre affect par une force.
Math matiquement, s'il n'y a pas de force ($F$),
| $ F =0$ |
alors a vitesse ($v$) est constant :
| $$ |
En rigueur stricte, l'absence de force implique que le moment est constant. Dans le cas o la masse est constante, un moment constant implique galement une vitesse constante.
(ID 15536)
Si un crayon graphite est tir d\'un canon haute vitesse, il se comporte comme s\'il tait hautement rigide et peut p n trer des planches de bois sans tre endommag

(ID 2882)
Si une simple paille est tir e d\'un canon haute vitesse, elle devient si rigide qu\'elle peut p n trer des objets comme une pomme de terre sans tre endommag e ni pli e:

(ID 2883)
Si la nappe est retir e suffisamment rapidement sous la vaisselle, par inertie, la vaisselle restera en place et retombera simplement sur la table une fois la nappe retir e. Si le processus est effectu lentement, la vaisselle suivra la nappe et finira par tomber sur le sol.

(ID 2881)
Tout joueur de Jenga qui r ussit sait que la seule fa on d\' viter que la tour ne tombe est de retirer les blocs avec de petits coups rapides qui enl vent les l ments rapidement, plut t que de les d placer lentement. La raison en est que le mouvement lent des blocs rend la tour instable et peut ventuellement la faire tomber. Cependant, si le mouvement est effectu rapidement, gr ce l\'inertie, la tour reste debout et quand elle commence r agir, elle est d j dans une position stable.

(ID 2880)
La navette spatiale tait un programme de la NASA con u pour permettre un vaisseau spatial d\'atteindre l\'orbite, de r aliser des op rations telles que le d ploiement, la r paration ou la r cup ration d\'un satellite, et de retourner sur la surface de la Terre. Au cours du processus, seul le r servoir principal de carburant tait perdu, les deux propulseurs mont s sur ses c t s tant r cup r s via un parachute apr s une chute. Le r servoir tait isol avec une couche protectrice, car le carburant devait tre maintenu basse temp rature.

L\'un des accidents mortels du programme des navettes spatiales s\'est produit lorsqu\'un morceau d\'isolation du r servoir principal de carburant s\'est d tach lors du d collage. Le morceau, de la taille d\'une brique, avait la consistance de mousse de plastique, mais en raison de la grande vitesse laquelle il se d pla ait, son inertie l\'a transform en un objet rigide. En cons quence, lorsqu\'il a heurt l\'aile de la navette spatiale, il a cr un trou plusieurs fois plus grand que l\'objet lui-m me. Ce dommage est pass inaper u, et lorsque la navette est revenue dans l\'atmosph re une semaine plus tard, les gaz incandescents cr s par la friction avec l\'atmosph re ont caus la d sint gration de l\'aile. Cela a rendu la navette incontr lable et elle s\'est cras e.

(ID 13999)
Si aucune force n'agit sur un corps, son moment d'inertie restera constant. Cela signifie que le produit de a masse d'inertie ($m_i$) et a vitesse ($v$) restera constant. En d'autres termes, si la masse augmente, la vitesse diminuera, et vice-versa. Pour comprendre pourquoi cela se produit, imaginez un chariot avec une certaine masse et vitesse auquel une masse suppl mentaire est ajout e. Cette masse suppl mentaire est initialement au repos dans notre syst me et n'a donc pas de moment. Le chariot doit transf rer une partie de son moment la nouvelle masse pour qu'elle acqui re la m me vitesse, ce qui entra ne une perte de moment et, par cons quent, une r duction de la vitesse du chariot :
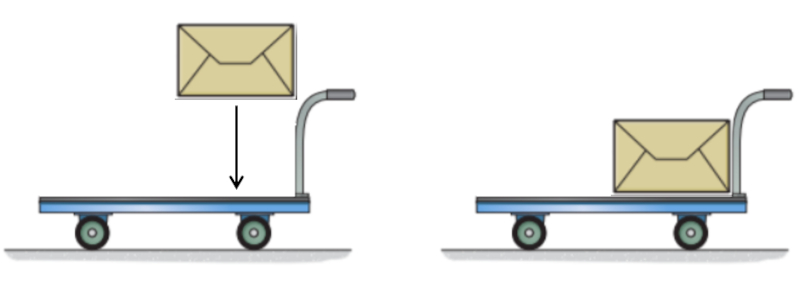
Inversement, si nous lan ons une masse depuis un chariot en mouvement de mani re ce qu'elle s'arr te compl tement, nous r cup rons le moment que cette masse poss dait, augmentant ainsi le moment du chariot et donc sa vitesse. Cela ne peut se produire que si la masse s'arr te lorsqu'elle est lanc e ; si elle est simplement lib r e, elle continuera de se d placer la m me vitesse.
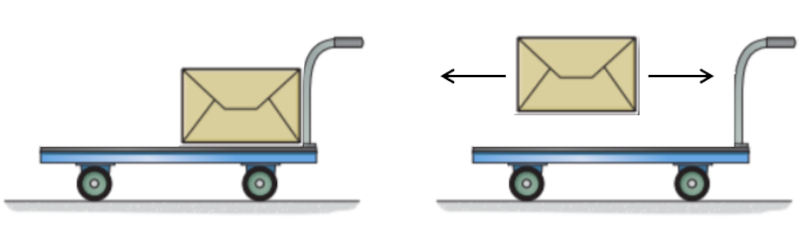
Ce dernier processus aide galement comprendre la troisi me loi de Newton sur l'action et la r action, car en agissant sur la masse lib r e, nous r coltons la r action correspondante.
(ID 3238)
(ID 15474)
ID:(754, 0)
