Inertia
Storyboard 
If no external force acts on an object, it will tend to maintain its current state, meaning that its velocity remains constant.This phenomenon is known as inertia and gives rise to Newton's first law, which generalizes this idea by stating that objects tend to maintain a constant momentum, which in the case of constant mass reduces to constant velocity.
ID:(754, 0)
Inertial mass concept
Concept 
Every object has inertia, which means it resists changes in its state. The state is associated with the velocity it possesses, while the inertia itself is associated with both the velocity and the so-called inertial mass. Although mass coincides with the value determined by a scale (gravitational mass), its physical meaning is different since inertia occurs even in situations where there is no gravity.To determine its value, one must measure how much force accelerates a body. However, it is common to assume the value by simply measuring the second, since it coincides with the value of gravitational mass. The measurement of inertial mass, like gravitational mass, is expressed in kilograms (MKS system).
ID:(2879, 0)
Newton's First Law
Concept 
Inertia refers to the tendency of bodies to maintain their current state. That is, it requires a force to change their velocity. If the applied force is very small, it will have no effect on the bodies. For example, consider tableware on a table: if the objects slide easily on the tablecloth, the tablecloth can be quickly removed without the dishes moving.
One consequence of inertia is that every body will maintain its state, whether at rest or in uniform motion in a straight line, unless acted upon by a force.
Mathematically, if there is no force ($F$),
| $ F =0$ |
then the speed ($v$) is constant:
| $$ |
In strict rigor, the absence of force implies that momentum is constant. For the case where mass is constant, constant momentum implies constant velocity.
ID:(15536, 0)
Pencil as projectile
Description 
If a graphite pencil is fired from a cannon at high velocity, it behaves as if it were highly rigid and can penetrate wooden boards without damage:

ID:(2882, 0)
Straws like projectiles
Description 
If a simple straw is fired from a cannon at high velocity, it becomes so rigid that it can penetrate objects like a potato without being damaged or bent:

ID:(2883, 0)
Remove the tablecloth without moving the dishes
Description 
If the tablecloth is pulled out from under the dishes quickly enough, the dishes will remain in place due to inertia and simply \'fall\' back onto the table once the tablecloth is removed. If the process is done slowly, the dishes will follow the tablecloth and end up on the floor.

ID:(2881, 0)
How to play Jenga
Description 
Every successful Jenga player knows that the only way to prevent the tower from falling is to remove blocks with small, quick taps rather than by slowly moving them. The reason for this is that the slow movement of blocks causes the tower to become unstable and potentially fall. However, if the movement is done quickly, due to inertia, the tower remains standing and by the time it starts to react, it is already in a stable position.

ID:(2880, 0)
Space Shuttle
Description 
The Space Shuttle was a NASA program designed to allow a spacecraft to reach orbit, perform operations such as deploying, repairing, or retrieving a satellite, and return to Earth\'s surface. In the process, only the main fuel tank was lost, with the two boosters mounted on its sides being recovered via parachute after a fall. The tank was insulated with a protective layer, as the fuel had to be kept at low temperatures.

One of the fatal accidents of the Space Shuttle program occurred when a piece of the main fuel tank\'s insulation broke off during liftoff. The piece, the size of a brick, had the consistency of foam plastic, but due to the high speed it was traveling, its inertia turned it into a rigid object. As a result, when it struck the shuttle wing, it created a hole several times larger than the object itself. This damage went undetected, and when the spacecraft re-entered the atmosphere a week later, the incandescent gases created by friction with the atmosphere caused the wing to disintegrate. This rendered the spacecraft uncontrollable and it crashed.

ID:(13999, 0)
Inertia
Model 
If no external force acts on an object, it will tend to maintain its current state, meaning that its velocity remains constant. This phenomenon is known as inertia and gives rise to Newton's first law, which generalizes this idea by stating that objects tend to maintain a constant momentum, which in the case of constant mass reduces to constant velocity.
Variables
Calculations
Calculations
Equations
(ID 4355)
(ID 10283)
(ID 10283)
(ID 15538)
Examples
(ID 15472)
Every object has inertia, which means it resists changes in its state. The state is associated with the velocity it possesses, while the inertia itself is associated with both the velocity and the so-called inertial mass. Although mass coincides with the value determined by a scale (gravitational mass), its physical meaning is different since inertia occurs even in situations where there is no gravity.To determine its value, one must measure how much force accelerates a body. However, it is common to assume the value by simply measuring the second, since it coincides with the value of gravitational mass. The measurement of inertial mass, like gravitational mass, is expressed in kilograms (MKS system).
(ID 2879)
Inertia refers to the tendency of bodies to maintain their current state. That is, it requires a force to change their velocity. If the applied force is very small, it will have no effect on the bodies. For example, consider tableware on a table: if the objects slide easily on the tablecloth, the tablecloth can be quickly removed without the dishes moving.
One consequence of inertia is that every body will maintain its state, whether at rest or in uniform motion in a straight line, unless acted upon by a force.
Mathematically, if there is no force ($F$),
| $ F =0$ |
then the speed ($v$) is constant:
| $$ |
In strict rigor, the absence of force implies that momentum is constant. For the case where mass is constant, constant momentum implies constant velocity.
(ID 15536)
If a graphite pencil is fired from a cannon at high velocity, it behaves as if it were highly rigid and can penetrate wooden boards without damage:

(ID 2882)
If a simple straw is fired from a cannon at high velocity, it becomes so rigid that it can penetrate objects like a potato without being damaged or bent:

(ID 2883)
If the tablecloth is pulled out from under the dishes quickly enough, the dishes will remain in place due to inertia and simply \'fall\' back onto the table once the tablecloth is removed. If the process is done slowly, the dishes will follow the tablecloth and end up on the floor.

(ID 2881)
Every successful Jenga player knows that the only way to prevent the tower from falling is to remove blocks with small, quick taps rather than by slowly moving them. The reason for this is that the slow movement of blocks causes the tower to become unstable and potentially fall. However, if the movement is done quickly, due to inertia, the tower remains standing and by the time it starts to react, it is already in a stable position.

(ID 2880)
The Space Shuttle was a NASA program designed to allow a spacecraft to reach orbit, perform operations such as deploying, repairing, or retrieving a satellite, and return to Earth\'s surface. In the process, only the main fuel tank was lost, with the two boosters mounted on its sides being recovered via parachute after a fall. The tank was insulated with a protective layer, as the fuel had to be kept at low temperatures.

One of the fatal accidents of the Space Shuttle program occurred when a piece of the main fuel tank\'s insulation broke off during liftoff. The piece, the size of a brick, had the consistency of foam plastic, but due to the high speed it was traveling, its inertia turned it into a rigid object. As a result, when it struck the shuttle wing, it created a hole several times larger than the object itself. This damage went undetected, and when the spacecraft re-entered the atmosphere a week later, the incandescent gases created by friction with the atmosphere caused the wing to disintegrate. This rendered the spacecraft uncontrollable and it crashed.

(ID 13999)
If no force acts on a body, its moment of inertia will remain constant. This means that the product of the inertial Mass ($m_i$) and the speed ($v$) will stay constant. In other words, if the mass increases, the velocity will decrease, and vice versa. To understand why this happens, imagine a cart with a certain mass and velocity to which an additional mass is added. This added mass is initially at rest in our system and therefore has no momentum. The cart must transfer some of its momentum to the new mass so that it acquires the same velocity as the cart, resulting in a loss of momentum and a reduction in the cart's speed:
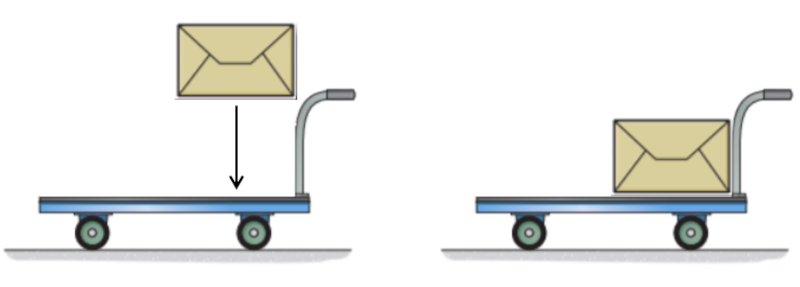
Conversely, if we throw a mass from a moving cart in such a way that the mass comes to a complete stop, we will recover the momentum that the mass had, thereby increasing the cart's momentum and, consequently, its speed. This can only happen if the mass stops when thrown; if it is simply released, it will continue moving at the same velocity.
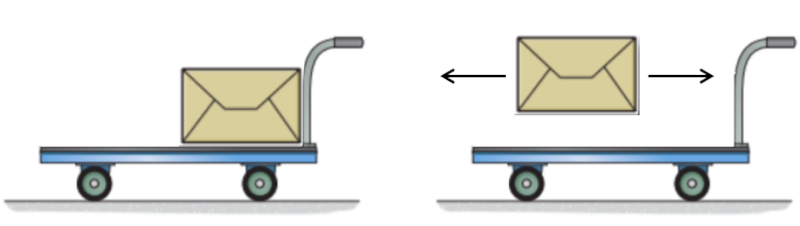
This last process also helps us understand the third law of action and reaction, as acting on the released mass allows us to harvest the corresponding reaction.
(ID 3238)
(ID 15474)
ID:(754, 0)
