Force visqueuse
Storyboard 
La force visqueuse est généralement modélisée comme étant proportionnelle à la vitesse de l'objet. La constante de la force visqueuse est proportionnelle à la viscosité du milieu et à des facteurs liés à la géométrie de l'objet.En l'absence d'une autre force agissant, la force visqueuse tend à ralentir un objet qui se déplace initialement avec une vitesse donnée.
ID:(1415, 0)
Force visqueuse sur un corps
Concept 
La force subie par un corps se déplaçant à une vitesse de ERROR:6029.1 dans un milieu caractérisé par a constante de force visqueuse ($b$) est a force visqueuse ($F_v$), comme décrit par l'équation :
| $ F_v = b v $ |
Pour comprendre le rôle de a constante de force visqueuse ($b$), il est important de se rappeler que la viscosité est une mesure de la manière dont le moment, ou la vitesse des molécules, se diffuse. En d'autres termes, a constante de force visqueuse ($b$) représente la mesure selon laquelle le corps perd de l'énergie en la transférant au milieu et en accélérant les molécules, leur fournissant ainsi de l'énergie. Par conséquent, a constante de force visqueuse ($b$) est proportionnel à la viscosité.
ID:(15546, 0)
Méthode d'Ostwald pour mesurer la viscosité
Description 
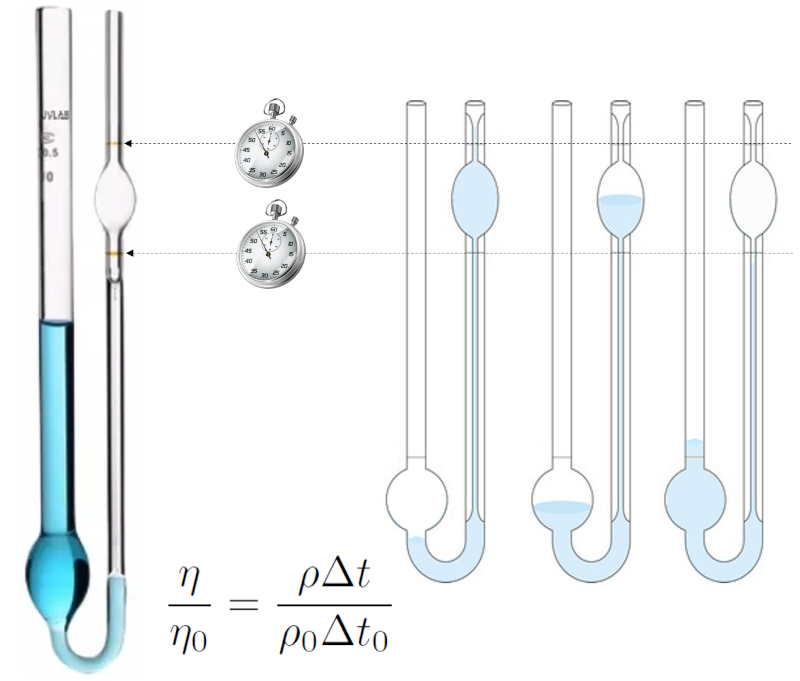
La méthode de mesure de la viscosité d'Ostwald est basée sur le comportement d'un liquide s'écoulant à travers un tube de petit rayon (capillaire).
Le liquide est introduit, une aspiration est appliquée pour dépasser la marque supérieure, puis il est laissé s'écouler, mesurant le temps qu'il faut pour que le niveau passe de la marque supérieure à la marque inférieure.
L'expérience est d'abord réalisée avec un liquide pour lequel la viscosité et la densité sont connues (par exemple, de l'eau distillée), puis avec le liquide pour lequel la viscosité doit être déterminée. Si les conditions sont identiques, le liquide qui s'écoule dans les deux cas sera similaire, et ainsi, le temps sera proportionnel à la densité divisée par la viscosité. Ainsi, une équation de comparaison entre les deux viscosités peut être établie :
ID:(15545, 0)
Vitesse en milieu visqueux
Concept 
Dans le cas d'un corps tombant dans un milieu visqueux, l'équation de mouvement est une équation de a vitesse ($v$) en fonction de le temps ($t$) avec a masse d'inertie ($m_i$) et a constante de force visqueuse ($b$) :
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Cela est obtenu avec a temps de viscosité et masse d'inertie ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
En intégrant avec un temps initial nul et a vitesse initiale ($v_0$),
| $ v = v_0 e^{- t / \tau_i }$ |
qui est représentée ci-dessous :
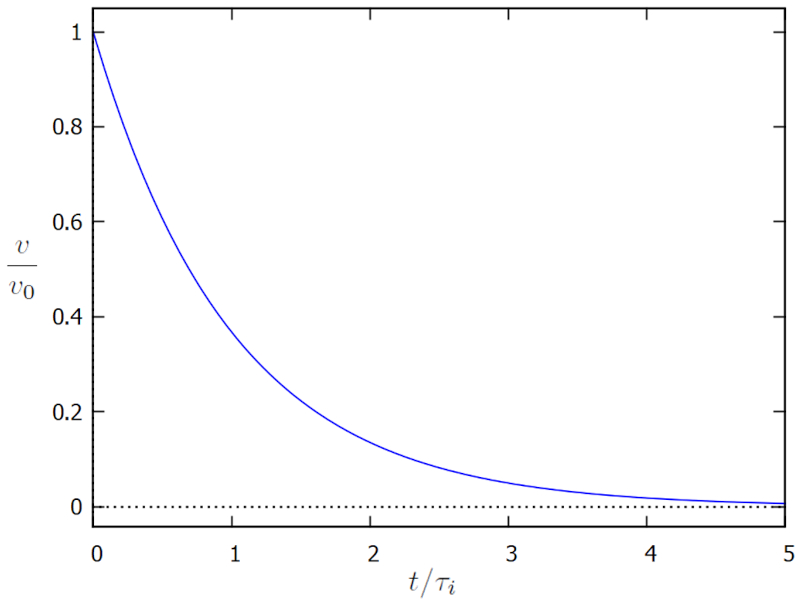
Le graphique illustre comment la viscosité force le corps à descendre jusqu'à zéro, ce qui se produit approximativement à un moment de l'ordre de a temps de viscosité et masse d'inertie ($\tau_i$).
ID:(15552, 0)
Chemin en milieu visqueux
Concept 
Dans le cas d'un corps tombant dans un milieu visqueux, l'équation de mouvement est une équation de a position ($s$) en fonction de a vitesse initiale ($v_0$), a temps de viscosité et masse d'inertie ($\tau_i$) et le temps ($t$) :
| $ \displaystyle\frac{ds}{dt} = v_0 e^{- t / \tau_i }$ |
À partir de cette équation, nous obtenons en intégrant avec un temps initial nul et une vitesse ($s_0$) :
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
qui est représentée ci-dessous :
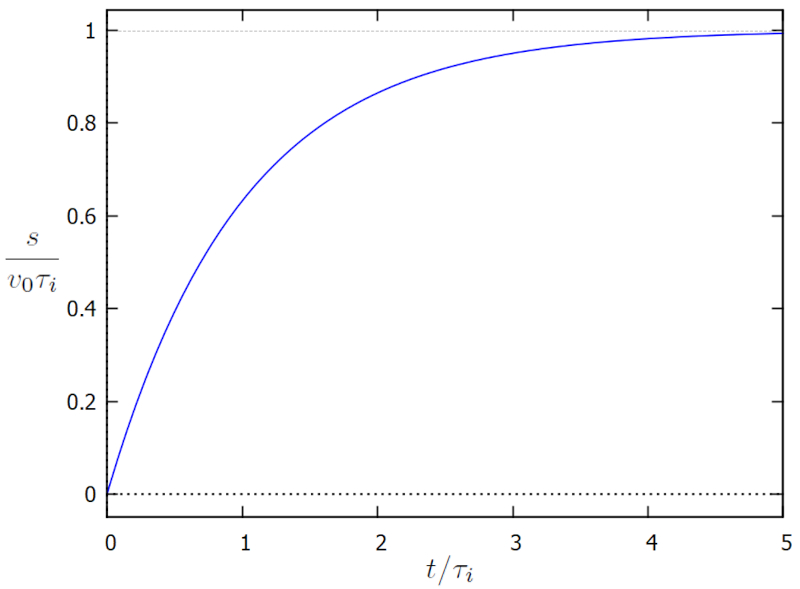
ID:(15551, 0)
Force visqueuse
Description 
La force visqueuse est généralement modélisée comme étant proportionnelle à la vitesse de l'objet. La constante de la force visqueuse est proportionnelle à la viscosité du milieu et à des facteurs liés à la géométrie de l'objet. En l'absence d'une autre force agissant, la force visqueuse tend à ralentir un objet qui se déplace initialement avec une vitesse donnée.
Variables
Calculs
Calculs
Équations
(ID 3243)
tant donn que le moment ($p$) est d fini avec a masse d'inertie ($m_i$) et a vitesse ($v$),
| $ p = m_i v $ |
Si a masse d'inertie ($m_i$) est gal a masse initiale ($m_0$), alors nous pouvons d river la quantit de mouvement par rapport au temps et obtenir a force à masse constante ($F$) :
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Par cons quent, nous en concluons que
| $ F = m_i a $ |
(ID 10975)
tant donn que la force totale a force à masse constante ($F$) est gale moins a force visqueuse ($F_v$) :
et que a force à masse constante ($F$) est compos e de a masse d'inertie ($m_i$) et a accélération instantanée ($a$) :
et que a force visqueuse ($F_v$) est compos e de a constante de force visqueuse ($b$) et a vitesse ($v$) :
nous obtenons
(ID 14498)
Avec a vitesse ($v$), le temps ($t$), a masse d'inertie ($m_i$) et a constante de force visqueuse ($b$), nous avons l' quation :
qui, avec a temps de viscosité et masse d'inertie ($\tau_i$) d fini par
peut tre r crite comme
$\displaystyle\frac{dv}{dt}=-\displaystyle\frac{v}{\tau_i}$
dont la solution est
(ID 14500)
(ID 15553)
Exemples
(ID 15522)
La force subie par un corps se d pla ant une vitesse de ERROR:6029.1 dans un milieu caract ris par a constante de force visqueuse ($b$) est a force visqueuse ($F_v$), comme d crit par l' quation :
| $ F_v = b v $ |
Pour comprendre le r le de a constante de force visqueuse ($b$), il est important de se rappeler que la viscosit est une mesure de la mani re dont le moment, ou la vitesse des mol cules, se diffuse. En d'autres termes, a constante de force visqueuse ($b$) repr sente la mesure selon laquelle le corps perd de l' nergie en la transf rant au milieu et en acc l rant les mol cules, leur fournissant ainsi de l' nergie. Par cons quent, a constante de force visqueuse ($b$) est proportionnel la viscosit .
(ID 15546)
La m thode de mesure de la viscosit d'Ostwald est bas e sur le comportement d'un liquide s' coulant travers un tube de petit rayon (capillaire).
Le liquide est introduit, une aspiration est appliqu e pour d passer la marque sup rieure, puis il est laiss s' couler, mesurant le temps qu'il faut pour que le niveau passe de la marque sup rieure la marque inf rieure.
L'exp rience est d'abord r alis e avec un liquide pour lequel la viscosit et la densit sont connues (par exemple, de l'eau distill e), puis avec le liquide pour lequel la viscosit doit tre d termin e. Si les conditions sont identiques, le liquide qui s' coule dans les deux cas sera similaire, et ainsi, le temps sera proportionnel la densit divis e par la viscosit . Ainsi, une quation de comparaison entre les deux viscosit s peut tre tablie :

(ID 15545)
Dans le cas d'un corps tombant dans un milieu visqueux, l' quation de mouvement est une quation de a vitesse ($v$) en fonction de le temps ($t$) avec a masse d'inertie ($m_i$) et a constante de force visqueuse ($b$) :
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Cela est obtenu avec a temps de viscosité et masse d'inertie ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
En int grant avec un temps initial nul et a vitesse initiale ($v_0$),
| $ v = v_0 e^{- t / \tau_i }$ |
qui est repr sent e ci-dessous :

Le graphique illustre comment la viscosit force le corps descendre jusqu' z ro, ce qui se produit approximativement un moment de l'ordre de a temps de viscosité et masse d'inertie ($\tau_i$).
(ID 15552)
Dans le cas d'un corps tombant dans un milieu visqueux, l' quation de mouvement est une quation de a position ($s$) en fonction de a vitesse initiale ($v_0$), a temps de viscosité et masse d'inertie ($\tau_i$) et le temps ($t$) :
| $ \displaystyle\frac{ds}{dt} = v_0 e^{- t / \tau_i }$ |
partir de cette quation, nous obtenons en int grant avec un temps initial nul et une vitesse ($s_0$) :
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
qui est repr sent e ci-dessous :

(ID 15551)
(ID 15534)
ID:(1415, 0)
