Inercia
Storyboard 
Si ningún agente actúa sobre un objeto, éste tenderá a mantener su estado actual, lo que implica que su velocidad permanece constante.
Este fenómeno se conoce como inercia y es la base del primer principio de Newton, que generaliza esta idea al afirmar que los objetos tienden a mantener constante su momento, que en el caso de una masa constante se reduce a una velocidad constante.
ID:(754, 0)
Concepto masa inercial
Imagen 
Todo objeto tiene inercia, lo que significa que se resiste a cambios en su estado. El estado se asocia con la velocidad que posee, mientras que la inercia en sí se asocia tanto con la velocidad como con la llamada masa inercial. Aunque la masa coincide con el valor determinado por una báscula (masa gravitacional), su significado físico es diferente ya que la inercia ocurre incluso en situaciones donde no hay gravedad.
Para determinar su valor, se debe medir cómo una fuerza acelera un cuerpo. Sin embargo, es común asumir el valor midiendo simplemente la masa gravitacional, ya que coincide con el valor de la masa inercial.
La medida de la masa inercial, al igual que la masa gravitacional, se expresa en kilogramos (sistema MKS).
ID:(2879, 0)
Primer principio de Newton
Nota 
La inercia se refiere a la tendencia de los cuerpos a mantener su estado actual, lo que significa que se requiere una fuerza para cambiar su velocidad. Si la fuerza aplicada es muy pequeña, no tendrá ningún efecto sobre los cuerpos. Por ejemplo, en una mesa cubierta por un mantel deslizante, se puede retirar rápidamente el mantel sin que los objetos de vajilla se muevan.
Una de las consecuencias de la inercia es que todo cuerpo mantendrá su estado, ya sea en reposo o en movimiento uniforme y en línea recta, a menos que una fuerza actúe sobre él.
Matemáticamente, si no hay fuerza ($F$),
| $ F =0$ |
se tiene que la velocidad ($v$) es constante:
| $$ |
En estricto rigor, la ausencia de fuerza implica que el momento es constante. Para el caso en que la masa sea constante, un momento constante implica que la velocidad también lo será.
ID:(15536, 0)
Lápiz como proyectil
Cita 
Si se dispara un lápiz de grafito con un cañón a alta velocidad, se comporta como si tuviera una alta rigidez y puede atravesar tableros de madera sin dañarse:

ID:(2882, 0)
Pajas como proyectiles
Ejercicio 
Si se dispara una simple paja con un cañón a alta velocidad, esta se vuelve tan rígida que puede penetrar objetos como una patata sin sufrir daños ni doblarse:

ID:(2883, 0)
Retirar el mantel sin mover la vajilla
Ecuación 
Si se retira lo suficientemente rápido el mantel debajo de la vajilla, por inercia la vajilla permanece en su lugar y simplemente \'cae\' sobre la mesa cuando el mantel ha sido retirado. Si el proceso se realiza lentamente, se le da tiempo a la vajilla para seguir al mantel y terminar en el suelo.

ID:(2881, 0)
Forma de jugar Jenga
Script 
Todo jugador exitoso de Jenga sabe que la única forma de evitar que la torre se caiga es sacar los bloques con pequeños golpes que remuevan los elementos rápidamente en lugar de moverlos lentamente. La razón de esto es que el movimiento lento de los bloques hace que la torre se vuelva inestable y potencialmente caiga. Sin embargo, si el movimiento se hace rápidamente, debido a la inercia, la torre permanece en pie y cuando empieza a reaccionar, ya se encuentra en una posición estable.

ID:(2880, 0)
Space Shuttle
Variable 
El transbordador espacial fue un programa creado para la nasa que permitía que una nave alcanzara una órbita, pudiera realizar operaciones como poner en órbita, reparar o recuperar un satélite y volver a la superficie de la tierra. En el proceso solo se perdía el estanque principal de combustible, siendo los dos propulsores montados a sus costados recuperados lego de una caída con paracaídas. El estanque llevaba una capa aislante protectora dado que el combustible tenia que ser mantenido a baja temperatura.

Uno de los accidentes fatales del programa de los Transbordadores Espaciales ocurrió cuando un trozo del revestimiento del tanque principal de combustible se desprendió durante el despegue. El trozo, del tamaño de un ladrillo, tenía la consistencia de espuma de plástico, pero debido a la alta velocidad a la que viajaba, su inercia lo convirtió en un objeto rígido. Como resultado, cuando impactó el ala del transbordador, creó un agujero varias veces más grande que el objeto mismo. Este daño no fue detectado, y cuando la nave volvió a entrar en la atmósfera una semana después, los gases incandescentes creados por la fricción con la atmósfera provocaron que el ala se desintegrara. Esto hizo que la nave fuera incontrolable y se estrellara.

ID:(13999, 0)
Inercia
Descripción 
Si ningún agente actúa sobre un objeto, éste tenderá a mantener su estado actual, lo que implica que su velocidad permanece constante. Este fenómeno se conoce como inercia y es la base del primer principio de Newton, que generaliza esta idea al afirmar que los objetos tienden a mantener constante su momento, que en el caso de una masa constante se reduce a una velocidad constante.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 4355)
(ID 10283)
(ID 10283)
(ID 15538)
Ejemplos
(ID 15472)
Todo objeto tiene inercia, lo que significa que se resiste a cambios en su estado. El estado se asocia con la velocidad que posee, mientras que la inercia en s se asocia tanto con la velocidad como con la llamada masa inercial. Aunque la masa coincide con el valor determinado por una b scula (masa gravitacional), su significado f sico es diferente ya que la inercia ocurre incluso en situaciones donde no hay gravedad.
Para determinar su valor, se debe medir c mo una fuerza acelera un cuerpo. Sin embargo, es com n asumir el valor midiendo simplemente la masa gravitacional, ya que coincide con el valor de la masa inercial.
La medida de la masa inercial, al igual que la masa gravitacional, se expresa en kilogramos (sistema MKS).
(ID 2879)
La inercia se refiere a la tendencia de los cuerpos a mantener su estado actual, lo que significa que se requiere una fuerza para cambiar su velocidad. Si la fuerza aplicada es muy peque a, no tendr ning n efecto sobre los cuerpos. Por ejemplo, en una mesa cubierta por un mantel deslizante, se puede retirar r pidamente el mantel sin que los objetos de vajilla se muevan.
Una de las consecuencias de la inercia es que todo cuerpo mantendr su estado, ya sea en reposo o en movimiento uniforme y en l nea recta, a menos que una fuerza act e sobre l.
Matem ticamente, si no hay fuerza ($F$),
| $ F =0$ |
se tiene que la velocidad ($v$) es constante:
| $$ |
En estricto rigor, la ausencia de fuerza implica que el momento es constante. Para el caso en que la masa sea constante, un momento constante implica que la velocidad tambi n lo ser .
(ID 15536)
Si se dispara un l piz de grafito con un ca n a alta velocidad, se comporta como si tuviera una alta rigidez y puede atravesar tableros de madera sin da arse:

(ID 2882)
Si se dispara una simple paja con un ca n a alta velocidad, esta se vuelve tan r gida que puede penetrar objetos como una patata sin sufrir da os ni doblarse:

(ID 2883)
Si se retira lo suficientemente r pido el mantel debajo de la vajilla, por inercia la vajilla permanece en su lugar y simplemente \'cae\' sobre la mesa cuando el mantel ha sido retirado. Si el proceso se realiza lentamente, se le da tiempo a la vajilla para seguir al mantel y terminar en el suelo.

(ID 2881)
Todo jugador exitoso de Jenga sabe que la nica forma de evitar que la torre se caiga es sacar los bloques con peque os golpes que remuevan los elementos r pidamente en lugar de moverlos lentamente. La raz n de esto es que el movimiento lento de los bloques hace que la torre se vuelva inestable y potencialmente caiga. Sin embargo, si el movimiento se hace r pidamente, debido a la inercia, la torre permanece en pie y cuando empieza a reaccionar, ya se encuentra en una posici n estable.

(ID 2880)
El transbordador espacial fue un programa creado para la nasa que permit a que una nave alcanzara una rbita, pudiera realizar operaciones como poner en rbita, reparar o recuperar un sat lite y volver a la superficie de la tierra. En el proceso solo se perd a el estanque principal de combustible, siendo los dos propulsores montados a sus costados recuperados lego de una ca da con paraca das. El estanque llevaba una capa aislante protectora dado que el combustible tenia que ser mantenido a baja temperatura.

Uno de los accidentes fatales del programa de los Transbordadores Espaciales ocurri cuando un trozo del revestimiento del tanque principal de combustible se desprendi durante el despegue. El trozo, del tama o de un ladrillo, ten a la consistencia de espuma de pl stico, pero debido a la alta velocidad a la que viajaba, su inercia lo convirti en un objeto r gido. Como resultado, cuando impact el ala del transbordador, cre un agujero varias veces m s grande que el objeto mismo. Este da o no fue detectado, y cuando la nave volvi a entrar en la atm sfera una semana despu s, los gases incandescentes creados por la fricci n con la atm sfera provocaron que el ala se desintegrara. Esto hizo que la nave fuera incontrolable y se estrellara.

(ID 13999)
Si no act a una fuerza sobre un cuerpo, el momento de inercia permanecer constante. Esto significa que el producto de la masa inercial ($m_i$) y la velocidad ($v$) se mantendr constante. Es decir, si la masa aumenta, la velocidad se reducir , y viceversa. Para entender por qu ocurre esto, podemos imaginar un carro con una cierta masa y velocidad al que se le a ade una masa adicional que, en nuestro sistema, est en reposo y, por lo tanto, no tiene momento. El carro deber transferir parte de su momento a la nueva masa para que esta adquiera la misma velocidad que el carro, lo que resultar en una disminuci n del momento y, por lo tanto, de la velocidad del carro:
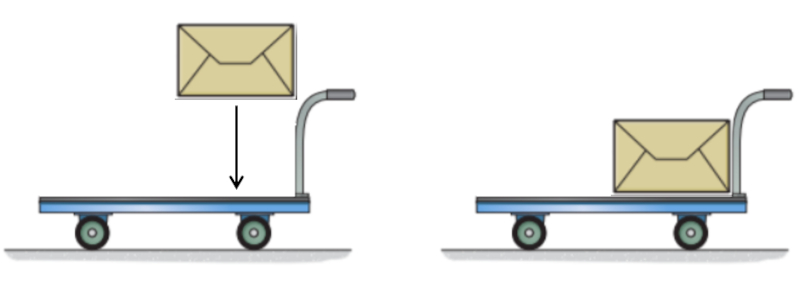
Por otro lado, si arrojamos una masa desde un carro en movimiento de manera que esta se detenga por completo, habremos recuperado el momento que la masa pose a, incrementando as el momento del carro y, con ello, su velocidad. Esto solo es posible si la masa se detiene al ser arrojada; si simplemente la dejamos "libre", continuar movi ndose a la misma velocidad.
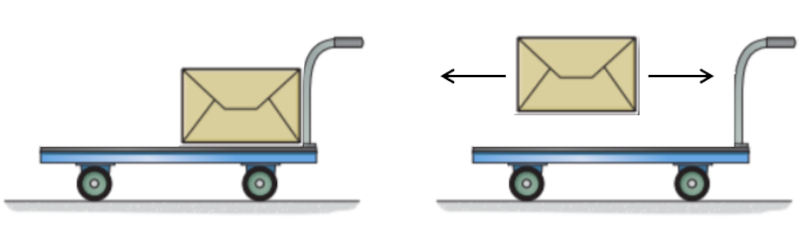
Este ltimo proceso tambi n nos ayuda a entender el tercer principio de la acci n y reacci n, ya que al actuar sobre la masa que liberamos, estamos obteniendo la reacci n correspondiente.
(ID 3238)
(ID 15474)
Si la fuerza con masa constante ($F$) es nula, entonces el momento ($p$) ser constante, es decir, igual a el momento inicial ($p_0$):
| $ p = p_0 $ |
(ID 15538)
El momento ($p$) se calcula a partir de la masa inercial ($m_i$) y la velocidad ($v$) mediante
| $ p = m_i v $ |
(ID 10283)
El momento ($p$) se calcula a partir de la masa inercial ($m_i$) y la velocidad ($v$) mediante
| $ p = m_i v $ |
(ID 10283)
La aceleraci n se define como la variaci n de la velocidad por unidad de tiempo.
Por lo tanto, es necesario establecer la diferencia de velocidad ($\Delta v$) en funci n de la velocidad ($v$) y la velocidad inicial ($v_0$) de la siguiente manera:
| $ dv \equiv v - v_0 $ |
(ID 4355)
Si la masa inercial ($m_i$) var a, el momento se modifica a menos que la velocidad var e de manera inversa. Por esta raz n, es importante considerar la variación de la masa inercial ($\Delta m_i$), calculado a partir de la diferencia con la masa inicial ($m_0$) mediante:
| $ \Delta m_i = m_i - m_0 $ |
(ID 15537)
ID:(754, 0)
