Viscose force
Storyboard 
Viscous force is often modeled as proportional to the velocity of an object. The constant of viscous force is proportional to the viscosity of the medium and factors related to the geometry of the object.If no other force is acting, the viscous force tends to decelerate an object that is initially moving with a given velocity.
ID:(1415, 0)
Viscous force on a body
Concept 
The force experienced by a body moving at ERROR:6029.1 in a medium, characterized by the constant of the Viscose Force ($b$), is the viscose force ($F_v$), as described by the equation:
| $ F_v = b v $ |
To understand the role of the constant of the Viscose Force ($b$), it's important to remember that viscosity is a measure of how momentum, or the velocity of molecules, diffuses. In other words, the constant of the Viscose Force ($b$) represents the extent to which the body loses energy by transferring it to the medium and accelerating the molecules, thereby providing them with energy. Therefore, the constant of the Viscose Force ($b$) is proportional to viscosity.
ID:(15546, 0)
Ostwald method for measuring viscosity
Description 
The Ostwald viscosity measurement method is based on the behavior of a liquid flowing through a small-radius tube (capillary).
The liquid is introduced, suction is applied to exceed the upper mark, and then it is allowed to drain, measuring the time it takes for the level to pass from the upper to the lower mark.
The experiment is conducted first with a liquid for which viscosity and density are known (e.g., distilled water), and then with the liquid for which viscosity is to be determined. If conditions are identical, the liquid flowing in both cases will be similar, and thus, the time will be proportional to the density divided by the viscosity. Thus, a comparison equation between both viscosities can be established:
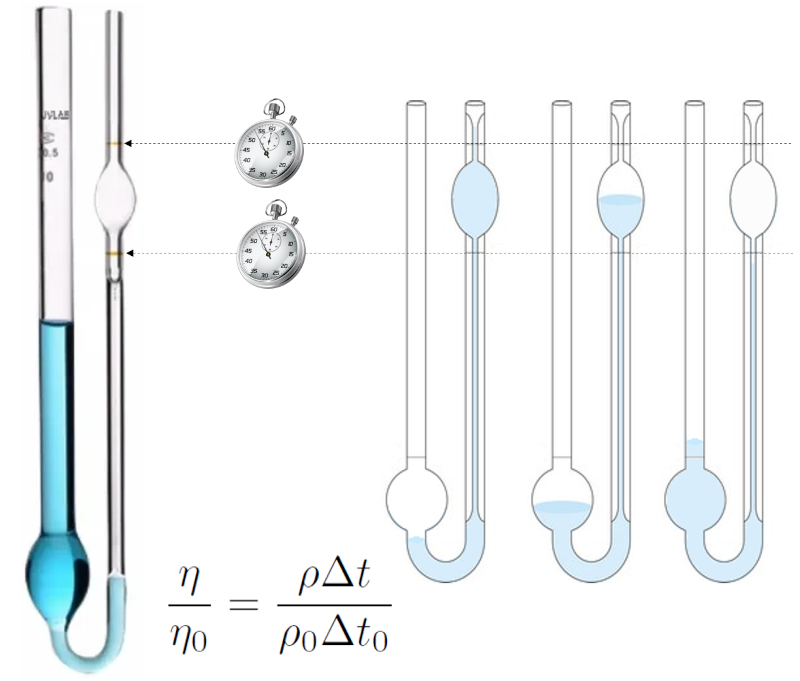
ID:(15545, 0)
Speed in viscous medium
Concept 
In the case of a body falling in a viscous medium, the equation of motion is an equation of the speed ($v$) as a function of the time ($t$) with the inertial Mass ($m_i$) and the constant of the Viscose Force ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
This is obtained with the viscosity time and inertial mass ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
Integrating with initial time zero and the initial Speed ($v_0$),
| $ v = v_0 e^{- t / \tau_i }$ |
which is represented below:
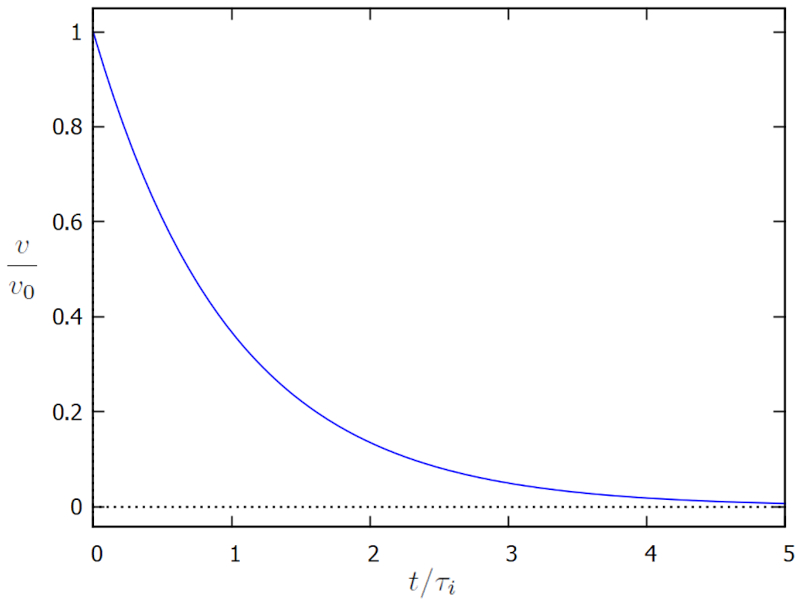
The graph illustrates how viscosity forces the body to descend to zero, which occurs approximately at a time of the order of the viscosity time and inertial mass ($\tau_i$).
ID:(15552, 0)
Path in viscous medium
Concept 
In the case of a body falling in a viscous medium, the equation of motion is an equation of the position ($s$) as a function of the initial Speed ($v_0$), the viscosity time and inertial mass ($\tau_i$) and the time ($t$):
| $ \displaystyle\frac{ds}{dt} = v_0 e^{- t / \tau_i }$ |
From this equation, we obtain by integrating with initial time zero and ERROR:5336.1:
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
which is represented below:
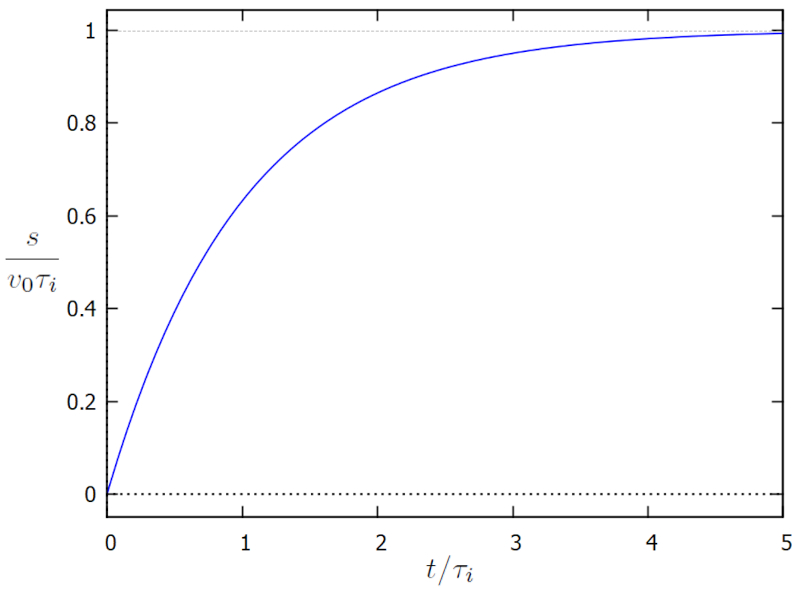
ID:(15551, 0)
Viscose force
Model 
Viscous force is often modeled as proportional to the velocity of an object. The constant of viscous force is proportional to the viscosity of the medium and factors related to the geometry of the object. If no other force is acting, the viscous force tends to decelerate an object that is initially moving with a given velocity.
Variables
Calculations
Calculations
Equations
(ID 3243)
Since the moment ($p$) is defined with the inertial Mass ($m_i$) and the speed ($v$),
| $ p = m_i v $ |
If the inertial Mass ($m_i$) is equal to the initial mass ($m_0$), then we can derive the momentum with respect to time and obtain the force with constant mass ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Therefore, we conclude that
| $ F = m_i a $ |
(ID 10975)
Given that the total force the force with constant mass ($F$) is equal to minus the viscose force ($F_v$):
and the force with constant mass ($F$) is composed of the inertial Mass ($m_i$) and the instant acceleration ($a$):
| $ F = m_i a $ |
and the viscose force ($F_v$) is composed of the constant of the Viscose Force ($b$) and the speed ($v$):
| $ F_v = b v $ |
we obtain
| $ m_i a = - b v $ |
(ID 14498)
With the speed ($v$), the time ($t$), the inertial Mass ($m_i$), and the constant of the Viscose Force ($b$), we have the equation:
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
which, with the viscosity time and inertial mass ($\tau_i$) defined by
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
can be rewritten as
$\displaystyle\frac{dv}{dt}=-\displaystyle\frac{v}{\tau_i}$
whose solution is
| $ v = v_0 e^{- t / \tau_i }$ |
(ID 14500)
(ID 15553)
Examples
(ID 15522)
The force experienced by a body moving at ERROR:6029.1 in a medium, characterized by the constant of the Viscose Force ($b$), is the viscose force ($F_v$), as described by the equation:
| $ F_v = b v $ |
To understand the role of the constant of the Viscose Force ($b$), it's important to remember that viscosity is a measure of how momentum, or the velocity of molecules, diffuses. In other words, the constant of the Viscose Force ($b$) represents the extent to which the body loses energy by transferring it to the medium and accelerating the molecules, thereby providing them with energy. Therefore, the constant of the Viscose Force ($b$) is proportional to viscosity.
(ID 15546)
The Ostwald viscosity measurement method is based on the behavior of a liquid flowing through a small-radius tube (capillary).
The liquid is introduced, suction is applied to exceed the upper mark, and then it is allowed to drain, measuring the time it takes for the level to pass from the upper to the lower mark.
The experiment is conducted first with a liquid for which viscosity and density are known (e.g., distilled water), and then with the liquid for which viscosity is to be determined. If conditions are identical, the liquid flowing in both cases will be similar, and thus, the time will be proportional to the density divided by the viscosity. Thus, a comparison equation between both viscosities can be established:

(ID 15545)
In the case of a body falling in a viscous medium, the equation of motion is an equation of the speed ($v$) as a function of the time ($t$) with the inertial Mass ($m_i$) and the constant of the Viscose Force ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
This is obtained with the viscosity time and inertial mass ($\tau_i$)
| $ \tau \equiv \displaystyle\frac{ m_i }{ b }$ |
Integrating with initial time zero and the initial Speed ($v_0$),
| $ v = v_0 e^{- t / \tau_i }$ |
which is represented below:

The graph illustrates how viscosity forces the body to descend to zero, which occurs approximately at a time of the order of the viscosity time and inertial mass ($\tau_i$).
(ID 15552)
In the case of a body falling in a viscous medium, the equation of motion is an equation of the position ($s$) as a function of the initial Speed ($v_0$), the viscosity time and inertial mass ($\tau_i$) and the time ($t$):
| $ \displaystyle\frac{ds}{dt} = v_0 e^{- t / \tau_i }$ |
From this equation, we obtain by integrating with initial time zero and ERROR:5336.1:
| $ s = s_0 + v_0 \tau_i (1 - e^{- t / \tau_i })$ |
which is represented below:

(ID 15551)
(ID 15534)
ID:(1415, 0)
