Force of a spring
Storyboard 
The force generated by a spring is directly proportional to its elongation.
The proportionality constant is referred to as the spring constant or Hooke's constant. Similarly, the relationship of this force is called Hooke's Law.
ID:(1414, 0)
Mechanisms
Iframe 
Mechanisms
ID:(15521, 0)
The resort
Image 
A spring is a coiled wire that can be elongated or compressed.
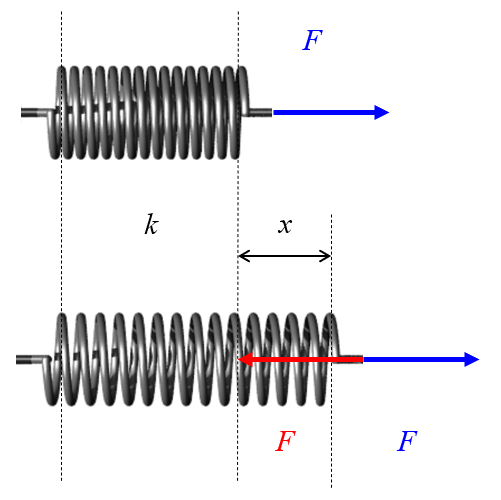
When these deformations are applied, the spring generates a force that opposes the motion.
ID:(12527, 0)
Hooke's law
Image 
Upon measuring the force required to achieve a given elongation in the spring, you'll notice that they are both proportional:

The spring is hung vertically, and known weights are added to it. The resulting elongation is measured, and a force vs. elongation graph is plotted. The slope, known as the spring's Hooke's constant, depends on the spring's properties.
The linearity of this relationship allows springs to be used as a method for measuring forces.
Force can be measured using a spring, with a scale established proportional to the elongation, directly indicating the associated force.
The instrument used to measure force using a spring is called a dynamometer (the 'dina' is the unit of force in the cgs system - centimeters, grams, seconds - such that 10^5 dynas equal one Newton).
ID:(11530, 0)
Study of spring behavior
Image 
To study how the spring elongates, it can be vertically suspended and gradually loaded with known weights.
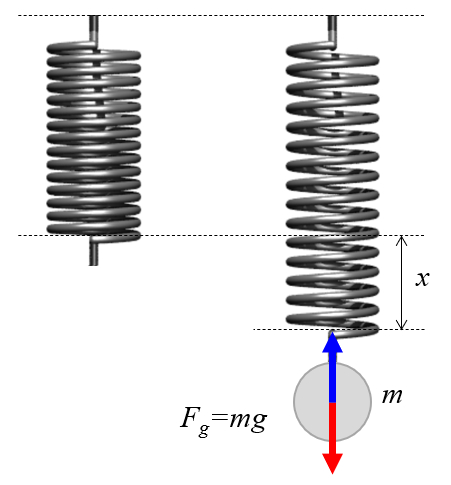
ID:(12528, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
$ F = F_k - F_g $
F = F_k - F_g
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_k = k x $
F_k = k * u
$ m_g = m_i $
m_g = m_i
$ m_i a = k x - m_g g $
m_i * a = k * x - m_g * g
$ \nu =\displaystyle\frac{1}{ T }$
nu =1/ T
$ \omega = 2 \pi \nu $
omega = 2* pi * nu
$ \omega = \displaystyle\frac{2 \pi }{ T }$
omega = 2* pi / T
$ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$
omega_0 ^2 = k / m_i
$ v = - x_0 \omega \sin \omega t + v_0 \cos \omega t $
v = - x_0 * omega_0 *sin( omega_0 * t )+ v_0 *cos( omega_0 * t )
$ x = x_0 \cos \omega t + \displaystyle\frac{ v_0 }{ \omega }\sin \omega t + \displaystyle\frac{ g }{ \omega ^2}$
x = x_0 *cos( omega_0 * t )+ v_0 *sin( omega_0 * t )/ omega_0 + g / omega_0 ^2
ID:(15533, 0)
Balance of spring and gravitational forces
Equation 
The equation of motion is established by the balance of forces, meaning that the force with constant mass ($F$) equals the elastic Force ($F_k$) minus the gravitational Force ($F_g$):
Si se cuelga una masa generando una fuerza
| $ F_g = m_g g $ |
a un resorte este último se dilata hasta generar una fuerza que es
que iguala a la fuerza gravitacional que es
| $ F = F_k - F_g $ |
ID:(15560, 0)
Force case constant mass
Equation 
In the case where the inertial Mass ($m_i$) equals the initial mass ($m_0$),
| $ m_g = m_i $ |
the derivative of momentum will be equal to the mass multiplied by the derivative of the speed ($v$). Since the derivative of velocity is the instant acceleration ($a$), we have that the force with constant mass ($F$) is
Since the moment ($p$) is defined with the inertial Mass ($m_i$) and the speed ($v$),
| $ p = m_i v $ |
If the inertial Mass ($m_i$) is equal to the initial mass ($m_0$), then we can derive the momentum with respect to time and obtain the force with constant mass ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Therefore, we conclude that
| $ F = m_i a $ |
ID:(10975, 0)
Hooke's Law
Equation 
The relationship between the elastic Force ($F_k$) and elongation the elongation ($u$) is written and referred to as Hooke's Law. The constant the hooke Constant ($k$) is called the spring constant:
ID:(3207, 0)
Gravitational Force
Equation 
The gravitational Force ($F_g$) is based on the gravitational mass ($m_g$) of the object and on a constant reflecting the intensity of gravity at the planet's surface. The latter is identified by the gravitational Acceleration ($g$), which is equal to $9.8 m/s^2$.
Consequently, it is concluded that:
ID:(3241, 0)
Spring equation of motion
Equation 
The equation of motion is derived directly from the equation of forces, where the force with constant mass ($F$) equals the elastic Force ($F_k$) minus the gravitational Force ($F_g$):
| $ F = F_k - F_g $ |
This equation is expressed in terms of the different forces involved, including the instant acceleration ($a$), the elongation of the Spring ($x$), the hooke Constant ($k$), the inertial Mass ($m_i$), the gravitational mass ($m_g$), and the gravitational Acceleration ($g$), as follows:
As the force with constant mass ($F$) equals the elastic Force ($F_k$) minus the gravitational Force ($F_g$):
| $ F = F_k - F_g $ |
Considering that the force with constant mass ($F$) with the inertial Mass ($m_i$) and the instant acceleration ($a$) is
| $ F = m_i a $ |
and the elastic Force ($F_k$) with the hooke Constant ($k$) and the elongation ($u$) is
| $ F_k = k x $ |
and that the gravitational Force ($F_g$) with the gravitational mass ($m_g$) and the gravitational Acceleration ($g$) is
| $ F_g = m_g g $ |
thus we get
| $ m_i a = k x - m_g g $ |
ID:(11293, 0)
Equality of inertial and gravitational mass
Equation 
The masses that Newton used in his principles are related to the inertia of bodies, which leads to the concept of the inertial Mass ($m_i$).
Newton's law, which is linked to the force between bodies due to their masses, is related to gravity, hence known as the gravitational mass ($m_g$).
Empirically, it has been concluded that both masses are equivalent, and therefore, we define
Einstein was the one who questioned this equality and, from that doubt, understood why both 'appear' equal in his theory of gravity. In his argument, Einstein explained that masses deform space, and this deformation of space causes a change in the behavior of bodies. Thus, masses turn out to be equivalent. The revolutionary concept of space curvature implies that even light, which lacks mass, is affected by celestial bodies, contradicting Newton's theory of gravitation. This was experimentally demonstrated by studying the behavior of light during a solar eclipse. In this situation, light beams are deflected due to the presence of the sun, allowing stars behind it to be observed.
ID:(12552, 0)
Oscillations with a spring
Equation 
The product of the hooke Constant ($k$) and the inertial Mass ($m_i$) is called the frecuencia angular del resorte ($\omega$) and is defined as:
ID:(1242, 0)
Angular frequency
Equation 
The angular frequency ($\omega$) is with the period ($T$) equal to
ID:(12335, 0)
Relación frecuencia angular - frecuencia
Equation 
Como la frecuencia angular es con angular frequency $rad/s$, period $s$ and pi $rad$ igual a
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
y la frecuencia con frequency $Hz$ and period $s$ igual a
| $ \nu =\displaystyle\frac{1}{ T }$ |
se tiene que con frequency $Hz$ and period $s$ igual a
ID:(12338, 0)
Frequency
Equation 
The frequency ($\nu$) corresponds to the number of times an oscillation occurs within one second. The period ($T$) represents the time it takes for one oscillation to occur. Therefore, the number of oscillations per second is:
Frequency is indicated in Hertz (Hz).
ID:(4427, 0)
Solution for position
Equation 
The variable the oscillation amplitude ($x$) evolves in the time ($t$) according to the equation of motion with the oscillator angular frequency ($\omega_0$) and the gravitational Acceleration ($g$), given by:
| $\displaystyle\frac{d v }{d t } = \displaystyle\frac{ k x }{ m_i }- g $ |
If we assume that the initial amplitude of the oscillation ($x_0$) and the oscillator initial speed ($v_0$) are the solution, we can write it as:
ID:(15564, 0)
Solution for speed
Equation 
To obtain the oscillator speed ($v$), simply derive the oscillation amplitude ($x$) with respect to the time ($t$), yielding:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Thus, with the initial amplitude of the oscillation ($x_0$), the initial Speed ($v_0$), and the oscillator angular frequency ($\omega_0$), we get:
ID:(15565, 0)
