Utilizador:
Relações adiabáticas
Storyboard 
As relações adiabáticas descrevem como as propriedades de um gás mudam durante um processo adiabático, onde não há troca de calor com o ambiente. Para um gás ideal, a pressão e o volume estão relacionados de tal forma que seu produto, elevado à potência do índice adiabático, permanece constante. Da mesma forma, a relação entre temperatura e volume segue que a temperatura, multiplicada pelo volume elevado a um menos o índice adiabático, é constante. A relação entre temperatura e pressão também segue um padrão similar, indicando que as mudanças de temperatura e pressão estão ligadas de maneira previsível durante os processos adiabáticos.
ID:(1481, 0)
Processo adiabático
Conceito
Quando um gás se expande rapidamente, as moléculas de vapor d'água não têm tempo suficiente para trocar energia com o ambiente, então nenhum calor é transferido, ou seja, la variação de calor ($\delta Q$) permanece constante:
$\delta Q = 0$
Os processos que são realizados sob esta condição são chamados de processos adiabáticos [1,2].
A expansão do gás requer que o sistema realize trabalho ou gere o diferencial de trabalho impreciso ($\delta W$). No entanto, a energia necessária para isso não pode vir de la energia interna ($U$), portanto, ela deve ser obtida a partir do calor. Como resultado, a temperatura do sistema diminui, o que se reflete em uma redução em la variação de calor ($\delta Q$).
Um exemplo típico desse processo é a formação de nuvens. Quando o ar sobe por convecção, ele se expande, realiza trabalho e esfria. A umidade presente no ar condensa, formando nuvens.
Por outro lado, quando trabalho é realizado sobre o sistema, trabalho positivo o diferencial de trabalho impreciso ($\delta W$) é realizado. No entanto, como la energia interna ($U$) não pode aumentar, a energia térmica em la variação de calor ($\delta Q$) aumenta, resultando em um aumento na temperatura do sistema.
Um exemplo comum desse processo é o uso de uma bomba. Se tentarmos inflar algo rapidamente, realizamos trabalho no sistema de maneira adiabática, levando a um aumento em la variação de calor ($\delta Q$) e, consequentemente, a um aquecimento.
[1] "Réflexions sur la puissance motrice du feu" (Reflexões sobre a força motriz do fogo), Sadi Carnot, 1824
[2] "Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen" (Sobre a força motriz do calor e as leis que dela podem ser derivadas para a teoria do calor), Rudolf Clausius, Annalen der Physik und Chemie, 1850
ID:(41, 0)
Relação de caso adiabático de temperatura e volume
Conceito
No caso adiabático, para temperatura absoluta ($T$) e o volume ($V$) com la constante de gás universal ($R$), la massa molar ($M_m$), o calor específico dos gases a volume constante ($c_V$), la variação de temperatura ($dT$) e la variação de volume ($dV$), temos a seguinte equação:
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
Ao introduzir o índice adiabático ($\kappa$), esta equação pode ser expressa como:
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Isso nos permite escrever a equação como:
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Se integramos essa expressão entre o volume no estado i ($V_i$) e o volume no estado f ($V_f$), bem como entre la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$), obtemos:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(15741, 0)
Relação de caso adiabático de pressão e volume
Conceito
Com os valores o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$), apresenta-se a seguinte relação:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Usando a equação dos gases com os parâmetros la pressão ($p$), o volume ($V$), o número de moles ($n$), la constante de gás universal ($R$) e la temperatura absoluta ($T$), obtemos a seguinte expressão:
| $ p V = n R T $ |
Esta equação descreve como, em um processo adiabático que varia de uma situação inicial para uma final em termos de la pressão ($p$) e o volume ($V$), se relaciona com la pressão no estado inicial ($p_i$) e la pressão em estado final ($p_f$) da seguinte maneira:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(15742, 0)
Relação de caso adiabático de temperatura e pressão
Conceito
Com os valores de o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$), estabelece-se a seguinte relação:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Ao utilizar a equação dos gases com os parâmetros la pressão ($p$), o volume ($V$), o número de moles ($n$), la constante de gás universal ($R$) e la temperatura absoluta ($T$), obtemos a seguinte expressão:
| $ p V = n R T $ |
Esta equação descreve como, em um processo adiabático que varia de uma situação inicial para uma final em termos de la pressão ($p$) e la temperatura absoluta ($T$), ela se relaciona com la pressão no estado inicial ($p_i$) e la pressão em estado final ($p_f$) da seguinte forma:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(15743, 0)
Comparação de diagrama VT isobárico e adiabático
Conceito
Quando comparamos a relação entre la temperatura absoluta ($T$) e o volume ($V$) no caso isotérmico (onde "iso" significa igual e "barico" refere-se à pressão), obtemos a seguinte equação para la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$), o volume no estado i ($V_i$) e o volume no estado f ($V_f$):
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
No caso adiabático, esta equação deve ser satisfeita com o índice adiabático ($\kappa$), o que nos leva à seguinte equação:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Se considerarmos $\kappa=1.4$, isso pode ser observado graficamente na seguinte representação:
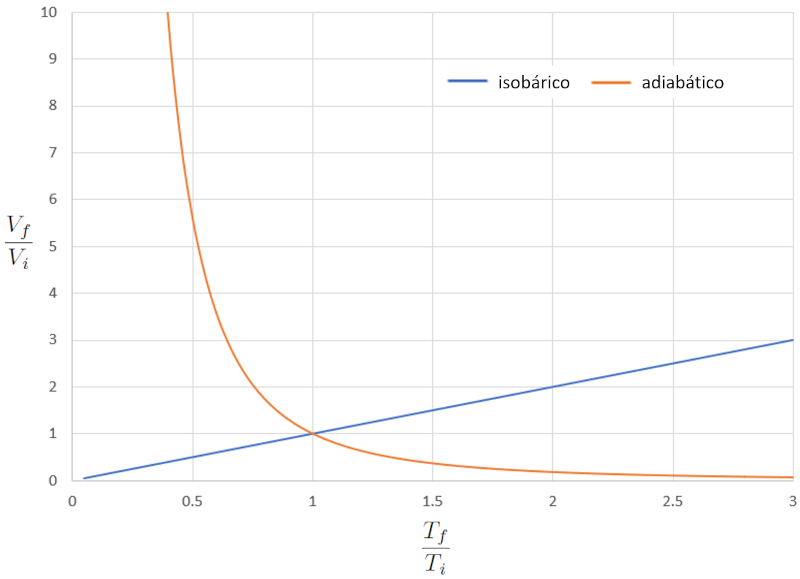
A grande diferença no comportamento de um gás em um processo isobárico em relação ao adiabático é que, no primeiro caso, se o sistema se expande, a temperatura aumenta, enquanto no segundo caso, ela diminui.
ID:(11172, 0)
Formação de nuvens por expansão adiabática
Conceito
Se água é colocada em uma garrafa e ar é bombeado para aumentar a pressão, obtém-se ar úmido de alta pressão. Quando a garrafa é aberta para o exterior, o ar se expande, causando uma redução na temperatura. Isso leva o ar a atingir o seu ponto de saturação, resultando na formação de vapor de água e na criação de uma nuvem.
ID:(11222, 0)
Comparação de diagramas pV isotérmicos e adiabáticos
Conceito
Quando comparamos a relação entre la pressão ($p$) e o volume ($V$) no caso isotérmico (iso = igual e térmico = temperatura), temos a seguinte equação para la pressão no estado inicial ($p_i$), la pressão em estado final ($p_f$), o volume no estado i ($V_i$) e o volume no estado f ($V_f$):
| $ p_i V_i = p_f V_f $ |
No caso adiabático, essa equação deve ser satisfeita com o índice adiabático ($\kappa$), levando à seguinte equação:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Se considerarmos $\kappa=1,4$, isso pode ser observado graficamente da seguinte forma:
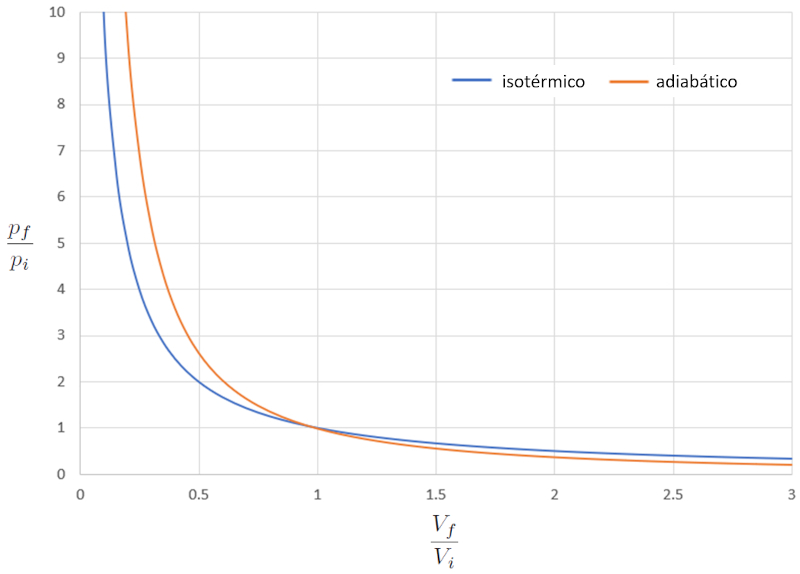
Em outras palavras, em um processo de compressão, se o processo for isotérmico, a resposta é mais suave em comparação com o caso adiabático, pois a pressão aumenta mais lentamente. Em um processo de expansão, o comportamento do gás em modo adiabático é mais suave.
ID:(11170, 0)
Quebrando um objeto com compressão adiabática
Conceito
Quando uma garrafa é golpeada em sua parte superior, a garrafa se desloca enquanto o líquido, devido à inércia, tende a ficar para trás. Isso cria um vácuo na parte inferior da garrafa, fazendo com que o líquido se acelere e, eventualmente, atinja o fundo da garrafa, resultando em sua ruptura. Esse fenômeno é conhecido como "martelo d'água" (water hammer). A reação adiabática do material, devido ao curto tempo de impacto, o torna mais rígido, o que contribui para esse efeito.
No entanto, no caso de uma bebida gaseificada, o líquido tende a ceder às bolhas de gás. Essas bolhas permitem que o líquido se contraia em vez de atingir o fundo da garrafa, evitando sua ruptura. Em vez disso, o líquido é expelido pelas bolhas geradas.
ID:(11223, 0)
Comparação de diagramas pT isocóricos e adiabáticos
Conceito
Quando comparamos a relação entre la temperatura absoluta ($T$) e la pressão ($p$) no caso isocórico (onde "iso" significa igual e "córico" se refere ao volume), obtemos a seguinte equação para la pressão no estado inicial ($p_i$), la pressão em estado final ($p_f$), la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$):
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
No caso adiabático, essa equação deve ser satisfeita com o índice adiabático ($\kappa$), o que nos leva à seguinte equação:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Se considerarmos $\kappa=1.4$, isso pode ser observado graficamente na seguinte representação:
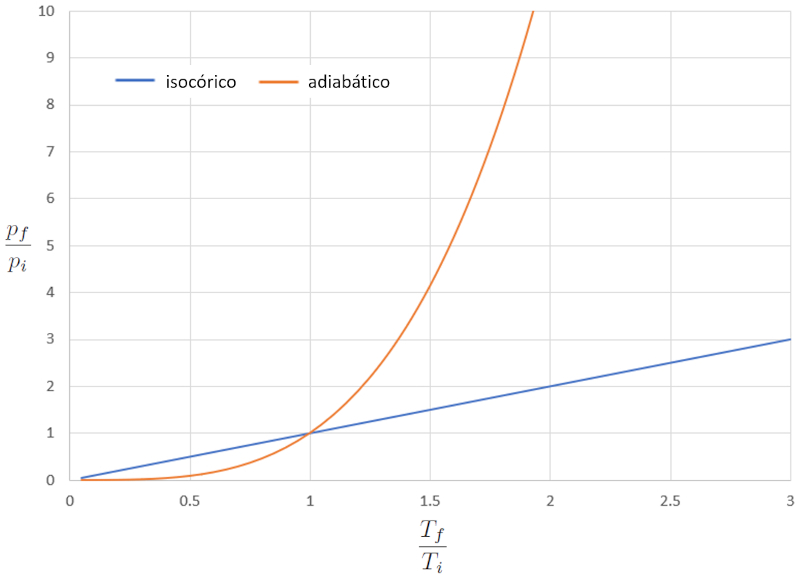
Nesse caso, a diferença significativa ocorre em temperaturas mais elevadas, onde a pressão aumenta dramaticamente. Em outras palavras, se aumentarmos drasticamente a pressão no caso adiabático, a temperatura varia apenas ligeiramente, enquanto no caso normal, ela aumenta significativamente.
ID:(11171, 0)
Incinerar um objeto com compressão adiabática
Conceito
Se um objeto for colocado em um recipiente de ar cuja pressão pode ser aumentada dramaticamente, ao realizar uma compressão adiabática, é possível elevar a temperatura a ponto de o material se incendiar espontaneamente.
ID:(11221, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \delta Q =0$
dQ =0
$ p_i V_i = n_i R T_i $
p * V = n * R * T
$ p_f V_f = n_f R T_f $
p * V = n * R * T
$ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$
p_i * V_i ^ kappa = p_f * V_f ^ kappa
$ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$
p_i ^(1- kappa )* T_i ^ kappa = p_f ^(1- kappa )* T_f ^ kappa
$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$
T_i * V_i ^( kappa -1)= T_f * V_f ^( kappa -1)
ID:(15324, 0)
Condição adiabática
Equação
No caso adiabático, o sistema não tem a capacidade de alterar o conteúdo calórico ($Q$), ou seja, o diferencial de calor impreciso ($\delta Q$) deve ser nulo:
| $ \delta Q =0$ |
ID:(4860, 0)
Relação de caso adiabático de temperatura e volume
Equação
De um estado inicial (i) com o volume no estado i ($V_i$) e la temperatura no estado inicial ($T_i$) vai para um estado final (f) com o volume no estado f ($V_f$) e la temperatura no estado final ($T_f$) var > com o índice adiabático ($\kappa$) de acordo com:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
No caso adiabático, para temperatura absoluta ($T$) e o volume ($V$) com la constante de gás universal ($R$), la massa molar ($M_m$), ($$), la variação de temperatura ($dT$) e la variação de volume ($dV$), temos a seguinte equação:
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
Ao introduzir o índice adiabático ($\kappa$), esta equação pode ser expressa como:
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Isso nos permite escrever a equação como:
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Se integramos essa expressão entre o volume no estado i ($V_i$) e o volume no estado f ($V_f$), bem como entre la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$), obtemos:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(4865, 0)
Relação de caso adiabático de pressão e volume
Equação
De um estado inicial (i) com la pressão em estado final ($p_f$) e o volume no estado i ($V_i$) vai para um estado final (f) com la pressão em estado final ($p_f$) e o volume no estado f ($V_f$) var > com o índice adiabático ($\kappa$) de acordo com:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Com os valores o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$), apresenta-se a seguinte relação:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Usando a equação dos gases com os parâmetros la pressão ($p$), o volume ($V$), o número de moles ($n$), la constante de gás universal ($R$) e la temperatura absoluta ($T$), obtemos a seguinte expressão:
| $ p V = n R T $ |
Esta equação descreve como, em um processo adiabático que varia de uma situação inicial para uma final em termos de la pressão ($p$) e o volume ($V$), se relaciona com la pressão no estado inicial ($p_i$) e la pressão em estado final ($p_f$) da seguinte maneira:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(4867, 0)
Relação de caso adiabático de temperatura e pressão
Equação
De um estado inicial (i) com la pressão no estado inicial ($p_i$) e la temperatura no estado inicial ($T_i$) vai para um estado final (f) com la pressão em estado final ($p_f$) e la temperatura no estado final ($T_f$) var > com o índice adiabático ($\kappa$) de acordo com:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Com os valores de o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$), estabelece-se a seguinte relação:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Ao utilizar a equação dos gases com os parâmetros la pressão ($p$), o volume ($V$), o número de moles ($n$), la constante de gás universal ($R$) e la temperatura absoluta ($T$), obtemos a seguinte expressão:
| $ p V = n R T $ |
Esta equação descreve como, em um processo adiabático que varia de uma situação inicial para uma final em termos de la pressão ($p$) e la temperatura absoluta ($T$), ela se relaciona com la pressão no estado inicial ($p_i$) e la pressão em estado final ($p_f$) da seguinte forma:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(4866, 0)
Lei específica do gás (1)
Equação
La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) estão relacionados pela seguinte equação:
| $ p_i V_i = n R T_i $ |
| $ p V = n R T $ |
La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) estão relacionados através das seguintes leis físicas:
• Lei de Boyle
| $ p V = C_b $ |
• Lei de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Lei de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Lei de Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Essas leis podem ser expressas de forma mais geral como:
$\displaystyle\frac{pV}{nT}=cte$
Essa relação geral estabelece que o produto da pressão e do volume dividido pelo número de moles e a temperatura permanece constante:
| $ p V = n R T $ |
onde la constante de gás universal ($R$) tem um valor de 8,314 J/K·mol.
ID:(3183, 1)
Lei específica do gás (2)
Equação
La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) estão relacionados pela seguinte equação:
| $ p_f V_f = n R T_f $ |
| $ p V = n R T $ |
La pressão ($p$), o volume ($V$), la temperatura absoluta ($T$) e o número de moles ($n$) estão relacionados através das seguintes leis físicas:
• Lei de Boyle
| $ p V = C_b $ |
• Lei de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Lei de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Lei de Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Essas leis podem ser expressas de forma mais geral como:
$\displaystyle\frac{pV}{nT}=cte$
Essa relação geral estabelece que o produto da pressão e do volume dividido pelo número de moles e a temperatura permanece constante:
| $ p V = n R T $ |
onde la constante de gás universal ($R$) tem um valor de 8,314 J/K·mol.
ID:(3183, 2)