Benützer:
Adiabatische Beziehungen
Storyboard 
Die adiabatischen Beziehungen beschreiben, wie sich die Eigenschaften eines Gases während eines adiabatischen Prozesses ändern, bei dem kein Wärmeaustausch mit der Umgebung stattfindet. Für ein ideales Gas sind Druck und Volumen so miteinander verbunden, dass ihr Produkt, erhöht auf die Potenz des adiabatischen Index, konstant bleibt. Ebenso folgt die Beziehung zwischen Temperatur und Volumen, dass die Temperatur multipliziert mit dem Volumen, erhöht um eins minus den adiabatischen Index, konstant ist. Auch die Beziehung zwischen Temperatur und Druck folgt einem ähnlichen Muster, was darauf hinweist, dass Temperatur- und Druckänderungen während adiabatischer Prozesse auf vorhersehbare Weise verbunden sind.
ID:(1481, 0)
Adiabatischen Prozess
Konzept
Wenn sich ein Gas schnell ausdehnt, haben die Wasserdampfmoleküle nicht genügend Zeit, Energie mit der Umgebung auszutauschen, sodass keine Wärme übertragen wird, d. h. Die Variation des Wärme ($\delta Q$) bleibt konstant:
$\delta Q = 0$
Die Prozesse, die unter dieser Bedingung ablaufen, werden adiabatische Prozesse genannt [1,2].
Die Expansion des Gases erfordert, dass das System Arbeit verrichtet oder der Differential ungenaue Arbeits ($\delta W$) erzeugt. Die für dies benötigte Energie kann jedoch nicht von die Innere Energie ($U$) stammen und muss daher aus Wärme gewonnen werden. Dies führt zu einer Abnahme der Temperatur des Systems und damit zu einer Abnahme von die Variation des Wärme ($\delta Q$).
Ein typisches Beispiel für diesen Prozess ist die Bildung von Wolken. Wenn Luft durch Konvektion aufsteigt, dehnt sie sich aus, verrichtet Arbeit und kühlt ab. Die Feuchtigkeit in der Luft kondensiert und bildet Wolken.
Umgekehrt, wenn Arbeit am System verrichtet wird, wird positive Arbeit der Differential ungenaue Arbeits ($\delta W$) geleistet. Da jedoch die Innere Energie ($U$) nicht zunehmen kann, steigt die thermische Energie in die Variation des Wärme ($\delta Q$) an, was zu einer Erhöhung der Temperatur des Systems führt.
Ein häufiges Beispiel für diesen Prozess ist die Verwendung einer Pumpe. Wenn wir versuchen, etwas schnell aufzublasen, verrichten wir adiabatisch Arbeit am System, was zu einer Erhöhung von die Variation des Wärme ($\delta Q$) und folglich zu einer Erwärmung führt.
[1] "Réflexions sur la puissance motrice du feu" (Reflexionen über die bewegende Kraft des Feuers), Sadi Carnot, 1824
[2] "Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen", Rudolf Clausius, Annalen der Physik und Chemie, 1850
ID:(41, 0)
Adiabatische Fallbeziehung von Temperatur und Volumen
Konzept
Im adiabatischen Fall, für Absolute Temperatur ($T$) und der Volumen ($V$) mit die Universelle Gas Konstante ($R$), die Molmasse ($M_m$), der Spezifische Wärme von Gasen bei konstantem Volumen ($c_V$), die Temperaturschwankungen ($dT$) und die Volumenvariation ($dV$), ergibt sich die folgende Gleichung:
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
Durch Einführung von der Adiabatischer Index ($\kappa$) kann diese Gleichung wie folgt ausgedrückt werden:
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Dies ermöglicht es uns, die Gleichung wie folgt zu schreiben:
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Wenn wir diesen Ausdruck zwischen der Volumen im Zustand i ($V_i$) und der Volumen im Zustand f ($V_f$) sowie zwischen die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) integrieren, erhalten wir:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(15741, 0)
Beziehung zwischen adiabatischem Druck und Volumenfall
Konzept
Mit den Werten der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) ergibt sich die folgende Beziehung:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Unter Verwendung der Gleichung für Gase mit den Parametern die Druck ($p$), der Volumen ($V$), der Anzahl der Mol ($n$), die Universelle Gas Konstante ($R$) und die Absolute Temperatur ($T$) erhalten wir den folgenden Ausdruck:
| $ p V = n R T $ |
Diese Gleichung beschreibt, wie sich in einem adiabatischen Prozess, der sich von einer Anfangssituation zu einer Endsituation in Bezug auf die Druck ($p$) und der Volumen ($V$) ändert, das Verhältnis zu die Druck im Ausgangszustand ($p_i$) und die Druck im Endzustand ($p_f$) wie folgt darstellt:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(15742, 0)
Adiabatische Fallbeziehung von Temperatur und Druck
Konzept
Mit den Werten der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) ergibt sich die folgende Beziehung:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Durch Anwendung der Gasgleichung mit den Parametern die Druck ($p$), der Volumen ($V$), der Anzahl der Mol ($n$), die Universelle Gas Konstante ($R$) und die Absolute Temperatur ($T$) erhalten wir den folgenden Ausdruck:
| $ p V = n R T $ |
Diese Gleichung beschreibt, wie sich in einem adiabatischen Prozess, der von einer Anfangssituation bis zu einer Endsituation in Bezug auf die Druck ($p$) und die Absolute Temperatur ($T$) variiert, die Beziehung zu die Druck im Ausgangszustand ($p_i$) und die Druck im Endzustand ($p_f$) wie folgt darstellt:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(15743, 0)
Vergleich des isobarisch und adiabatischen VT-Diagramms
Konzept
Wenn wir die Beziehung zwischen die Absolute Temperatur ($T$) und der Volumen ($V$) im isothermen Fall vergleichen (wo "iso" für gleich und "barisch" auf den Druck verweist), erhalten wir die folgende Gleichung für die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$), der Volumen im Zustand i ($V_i$) und der Volumen im Zustand f ($V_f$):
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Im adiabatischen Fall muss diese Gleichung mit der Adiabatischer Index ($\kappa$) erfüllt sein, was uns zu folgender Gleichung führt:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Wenn wir $\kappa=1,4$ berücksichtigen, kann dies grafisch in der folgenden Darstellung beobachtet werden:
Der große Unterschied im Verhalten eines Gases in einem isobaren Prozess im Vergleich zum adiabatischen Prozess besteht darin, dass im ersten Fall die Temperatur steigt, wenn sich ein System ausdehnt, während sie im zweiten Fall abnimmt.
ID:(11172, 0)
Wolkenbildung durch adiabatische Expansion
Konzept
Wenn Wasser in eine Flasche gegeben wird und Luft gepumpt wird, um den Druck zu erhöhen, entsteht feuchte, hochdruckhaltige Luft. Wenn die Flasche nach außen geöffnet wird, dehnt sich die Luft aus und es kommt zu einer Temperaturabnahme. Dies führt dazu, dass die Luft ihren Sättigungspunkt erreicht, was zur Bildung von Wasserdampf und der Entstehung einer Wolke führt.
Cloud in a Bottle - Sick Science! #076 (https://www.youtube.com/watch?v=LHjDT9pYxRA)
ID:(11222, 0)
Vergleich des isothermen und adiabatischen pV-Diagramms
Konzept
Wenn wir das Verhältnis zwischen die Druck ($p$) und der Volumen ($V$) im isothermen Fall (iso = gleich und thermisch = Temperatur) vergleichen, erhalten wir für die Druck im Ausgangszustand ($p_i$), die Druck im Endzustand ($p_f$), der Volumen im Zustand i ($V_i$) und der Volumen im Zustand f ($V_f$) die folgende Gleichung:
| $ p_i V_i = p_f V_f $ |
Im adiabatischen Fall muss diese Gleichung mit der Adiabatischer Index ($\kappa$) erfüllt sein, was zu folgender Gleichung führt:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Wenn wir $\kappa=1,4$ betrachten, kann dies grafisch wie folgt dargestellt werden:
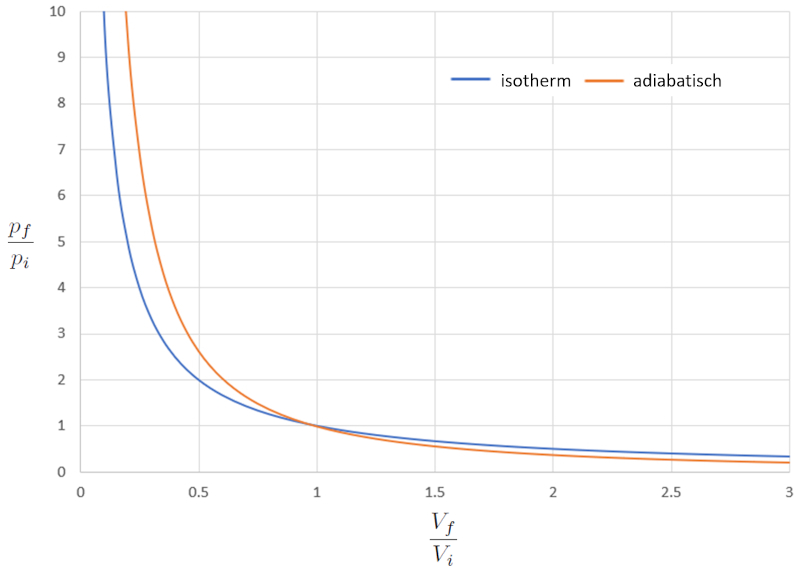
Mit anderen Worten, bei einem Kompressionsprozess ist die Antwort im isothermen Fall im Vergleich zum adiabatischen Fall sanfter, da der Druck langsamer ansteigt. Bei einem Expansionsprozess verhält sich das Gas im adiabatischen Modus sanfter.
ID:(11170, 0)
Brechen eines Objekts mit adiabatischer Kompression
Konzept
Wenn man eine Flasche oben schlägt, bewegt sich die Flasche, während die Flüssigkeit aufgrund der Trägheit dazu neigt, zurückzubleiben. Dies erzeugt ein Vakuum am Boden der Flasche, wodurch sich die Flüssigkeit beschleunigt und schließlich gegen den Boden der Flasche schlägt, was zu ihrer Zerstörung führt. Dieses Phänomen wird als "Wasserhammer" bezeichnet. Die kurze Dauer des Aufpralls führt zu einer adiabatischen Reaktion des Materials, wodurch es steifer wird und zum Wasserhammer-Effekt beiträgt.
Im Falle eines kohlensäurehaltigen Getränks hingegen neigt die Flüssigkeit dazu, den Gasblasen nachzugeben. Diese Blasen verhindern, dass die Flüssigkeit auf den Flaschenboden schlägt, und somit bleibt die Flasche intakt. Stattdessen wird die Flüssigkeit durch die entstandenen Blasen ausgestoßen.
Extrahiert aus WATER HAMMER (18,000FPS) | Why Does SODA Not Break the Bottle? (https://www.youtube.com/watch?v=tlRikG7FOdw)
ID:(11223, 0)
Vergleich des isochorisch und adiabatischen pT-Diagramms
Konzept
Wenn wir die Beziehung zwischen die Absolute Temperatur ($T$) und die Druck ($p$) im isochorischen Fall (wobei "iso" für gleich und "chorisch" für Volumen steht) vergleichen, erhalten wir die folgende Gleichung für die Druck im Ausgangszustand ($p_i$), die Druck im Endzustand ($p_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$):
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
Im adiabatischen Fall muss diese Gleichung mit der Adiabatischer Index ($\kappa$) erfüllt sein, was uns zu folgender Gleichung führt:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Wenn wir $\kappa=1.4$ betrachten, kann dies grafisch in der folgenden Darstellung beobachtet werden:
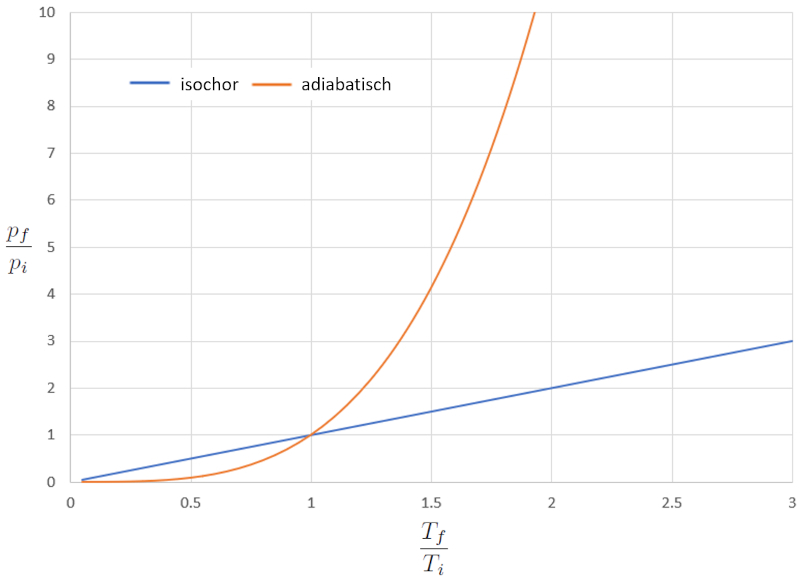
In diesem Fall tritt der signifikante Unterschied bei höheren Temperaturen auf, wo der Druck dramatisch ansteigt. Anders ausgedrückt, wenn wir den Druck im adiabatischen Fall drastisch erhöhen, variiert die Temperatur nur geringfügig, während sie im normalen Fall deutlich ansteigt.
ID:(11171, 0)
Verbrennen eines Objekt mit adiabatischer Kompression
Konzept
Wenn ein Objekt in einen Behälter mit Luft gelegt wird, dessen Druck dramatisch erhöht werden kann, kann durch eine adiabatische Kompression die Temperatur so weit ansteigen, dass das Material spontan entzündet wird.
Fire Syringe Demo (https://www.youtube.com/watch?v=OEwlwYqPIAw)
ID:(11221, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \delta Q =0$
dQ =0
$ p_i V_i = n_i R T_i $
p * V = n * R * T
$ p_f V_f = n_f R T_f $
p * V = n * R * T
$ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$
p_i * V_i ^ kappa = p_f * V_f ^ kappa
$ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$
p_i ^(1- kappa )* T_i ^ kappa = p_f ^(1- kappa )* T_f ^ kappa
$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$
T_i * V_i ^( kappa -1)= T_f * V_f ^( kappa -1)
ID:(15324, 0)
Adiabatischer Zustand
Gleichung
In einem adiabatischen Fall hat das System keine Möglichkeit, der Kaloriengehalt ($Q$) zu verändern, das bedeutet, dass der Differential ungenau Wärme ($\delta Q$) null sein muss:
| $ \delta Q =0$ |
ID:(4860, 0)
Adiabatische Fallbeziehung von Temperatur und Volumen
Gleichung
Von einem Anfangszustand (i) mit der Volumen im Zustand i ($V_i$) und die Temperatur im Ausgangszustand ($T_i$) geht es in einen Endzustand (f) mit der Volumen im Zustand f ($V_f$) und die Temperatur im Endzustand ($T_f$) gemäß:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Im adiabatischen Fall, für Absolute Temperatur ($T$) und der Volumen ($V$) mit die Universelle Gas Konstante ($R$), die Molmasse ($M_m$), der Spezifische Wärme bei konstantem Druck ($c_p$), die Temperaturschwankungen ($dT$) und die Volumenvariation ($dV$), ergibt sich die folgende Gleichung:
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
Durch Einführung von der Adiabatischer Index ($\kappa$) kann diese Gleichung wie folgt ausgedrückt werden:
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Dies ermöglicht es uns, die Gleichung wie folgt zu schreiben:
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Wenn wir diesen Ausdruck zwischen der Volumen im Zustand i ($V_i$) und der Volumen im Zustand f ($V_f$) sowie zwischen die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) integrieren, erhalten wir:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(4865, 0)
Beziehung zwischen adiabatischem Druck und Volumenfall
Gleichung
Von einem Anfangszustand (i) mit die Druck im Endzustand ($p_f$) und der Volumen im Zustand i ($V_i$) geht es in einen Endzustand (f) mit die Druck im Endzustand ($p_f$) und der Volumen im Zustand f ($V_f$) gemäß:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Mit den Werten der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) ergibt sich die folgende Beziehung:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Unter Verwendung der Gleichung für Gase mit den Parametern die Druck ($p$), der Volumen ($V$), der Anzahl der Mol ($n$), die Universelle Gas Konstante ($R$) und die Absolute Temperatur ($T$) erhalten wir den folgenden Ausdruck:
| $ p V = n R T $ |
Diese Gleichung beschreibt, wie sich in einem adiabatischen Prozess, der sich von einer Anfangssituation zu einer Endsituation in Bezug auf die Druck ($p$) und der Volumen ($V$) ändert, das Verhältnis zu die Druck im Ausgangszustand ($p_i$) und die Druck im Endzustand ($p_f$) wie folgt darstellt:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(4867, 0)
Adiabatische Fallbeziehung von Temperatur und Druck
Gleichung
Von einem Anfangszustand (i) mit die Druck im Ausgangszustand ($p_i$) und die Temperatur im Ausgangszustand ($T_i$) geht es in einen Endzustand (f) mit die Druck im Endzustand ($p_f$) und die Temperatur im Endzustand ($T_f$) gemäß:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Mit den Werten der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) ergibt sich die folgende Beziehung:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Durch Anwendung der Gasgleichung mit den Parametern die Druck ($p$), der Volumen ($V$), der Anzahl der Mol ($n$), die Universelle Gas Konstante ($R$) und die Absolute Temperatur ($T$) erhalten wir den folgenden Ausdruck:
| $ p V = n R T $ |
Diese Gleichung beschreibt, wie sich in einem adiabatischen Prozess, der von einer Anfangssituation bis zu einer Endsituation in Bezug auf die Druck ($p$) und die Absolute Temperatur ($T$) variiert, die Beziehung zu die Druck im Ausgangszustand ($p_i$) und die Druck im Endzustand ($p_f$) wie folgt darstellt:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(4866, 0)
Allgemeines Gasgesetz (1)
Gleichung
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) sind durch die folgende Gleichung verbunden:
| $ p_i V_i = n_i R T_i $ |
| $ p V = n R T $ |
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) stehen im Zusammenhang mit den folgenden physikalischen Gesetzen:
• Das Gesetz von Boyle
| $ p V = C_b $ |
• Das Gesetz von Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Das Gesetz von Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Das Gesetz von Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Diese Gesetze können in einer allgemeineren Form ausgedrückt werden:
$\displaystyle\frac{pV}{nT}=cte$
Diese allgemeine Beziehung besagt, dass das Produkt aus Druck und Volumen durch die Anzahl der Mol und die Temperatur geteilt konstant bleibt:
| $ p V = n R T $ |
wobei die Universelle Gas Konstante ($R$) einen Wert von 8,314 J/K·mol hat.
ID:(3183, 1)
Allgemeines Gasgesetz (2)
Gleichung
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) sind durch die folgende Gleichung verbunden:
| $ p_f V_f = n_f R T_f $ |
| $ p V = n R T $ |
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) stehen im Zusammenhang mit den folgenden physikalischen Gesetzen:
• Das Gesetz von Boyle
| $ p V = C_b $ |
• Das Gesetz von Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Das Gesetz von Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Das Gesetz von Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Diese Gesetze können in einer allgemeineren Form ausgedrückt werden:
$\displaystyle\frac{pV}{nT}=cte$
Diese allgemeine Beziehung besagt, dass das Produkt aus Druck und Volumen durch die Anzahl der Mol und die Temperatur geteilt konstant bleibt:
| $ p V = n R T $ |
wobei die Universelle Gas Konstante ($R$) einen Wert von 8,314 J/K·mol hat.
ID:(3183, 2)