Utilisateur:
Relations adiabatiques
Storyboard 
Les relations adiabatiques décrivent comment les propriétés d'un gaz changent lors d'un processus adiabatique, où il n'y a aucun échange de chaleur avec l'environnement. Pour un gaz idéal, la pression et le volume sont liés de telle manière que leur produit, élevé à la puissance de l'indice adiabatique, reste constant. De même, la relation entre la température et le volume suit que la température, multipliée par le volume élevé à un moins l'indice adiabatique, est constante. La relation entre température et pression suit également un schéma similaire, indiquant que les changements de température et de pression sont liés de manière prévisible pendant les processus adiabatiques.
ID:(1481, 0)
Processus adiabatique
Concept
Lorsqu'un gaz se dilate rapidement, les molécules de vapeur d'eau n'ont pas suffisamment de temps pour échanger de l'énergie avec l'environnement, donc aucune chaleur n'est transférée, c'est-à-dire que a variation de chaleur ($\delta Q$) reste constant :
$\delta Q = 0$
Les processus réalisés dans ces conditions sont appelés processus adiabatiques [1,2].
L'expansion du gaz nécessite que le système effectue un travail ou génère le différentiel de travail inexact ($\delta W$). Cependant, l'énergie nécessaire à cela ne peut pas provenir de a énergie interne ($U$), elle doit donc être obtenue à partir de la chaleur. En conséquence, la température du système diminue, ce qui se traduit par une diminution de a variation de chaleur ($\delta Q$).
Un exemple typique de ce processus est la formation de nuages. Lorsque l'air monte par convection, il se dilate, effectue un travail et se refroidit. L'humidité présente dans l'air se condense, formant ainsi des nuages.
Inversement, lorsque du travail est effectué sur le système, un travail positif le différentiel de travail inexact ($\delta W$) est effectué. Cependant, comme a énergie interne ($U$) ne peut pas augmenter, l'énergie thermique dans a variation de chaleur ($\delta Q$) augmente, entraînant une augmentation de la température du système.
Un exemple courant de ce processus est l'utilisation d'une pompe. Si nous essayons de gonfler quelque chose rapidement, nous effectuons un travail sur le système de manière adiabatique, ce qui entraîne une augmentation de a variation de chaleur ($\delta Q$) et donc un chauffage.
[1] "Réflexions sur la puissance motrice du feu", Sadi Carnot, 1824
[2] "Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen" (Sur la force motrice de la chaleur et les lois qui en découlent pour la théorie de la chaleur elle-même), Rudolf Clausius, Annalen der Physik und Chemie, 1850
ID:(41, 0)
Relation de cas adiabatique de la température et du volume
Concept
Dans le cas adiabatique, pour température absolue ($T$) et le volume ($V$) avec a constante du gaz universel ($R$), a masse molaire ($M_m$), le chaleur spécifique des gaz à volume constant ($c_V$), a variation de température ($dT$) et a variation de volume ($dV$), nous avons l'équation suivante :
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
En introduisant le indice adiabatique ($\kappa$), cette équation peut être exprimée comme suit :
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Cela nous permet d'écrire l'équation comme suit :
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Si nous intégrons cette expression entre le volume à l'état i ($V_i$) et le volume à l'état f ($V_f$), ainsi qu'entre a température à l'état initial ($T_i$) et a température à l'état final ($T_f$), nous obtenons :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(15741, 0)
Relation de cas adiabatique de la pression et du volume
Concept
Avec les valeurs le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$) et le indice adiabatique ($\kappa$), la relation suivante est présentée :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
En utilisant l'équation des gaz avec les paramètres a pression ($p$), le volume ($V$), le nombre de taupes ($n$), a constante du gaz universel ($R$) et a température absolue ($T$), nous obtenons l'expression suivante :
| $ p V = n R T $ |
Cette équation décrit comment, dans un processus adiabatique variant d'une situation initiale à une situation finale en termes de a pression ($p$) et le volume ($V$), elle est reliée à A pression à l'état initial ($p_i$) et a pression à l'état final ($p_f$) de la manière suivante :
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(15742, 0)
Relation de cas adiabatique de la température et de la pression
Concept
Com os valores de le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$) e le indice adiabatique ($\kappa$), estabelece-se a seguinte relação:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Ao utilizar a equação dos gases com os parâmetros a pression ($p$), le volume ($V$), le nombre de taupes ($n$), a constante du gaz universel ($R$) e a température absolue ($T$), obtemos a seguinte expressão:
| $ p V = n R T $ |
Esta equação descreve como, em um processo adiabático que varia de uma situação inicial para uma final em termos de a pression ($p$) e a température absolue ($T$), ela se relaciona com a pression à l'état initial ($p_i$) e a pression à l'état final ($p_f$) da seguinte forma:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(15743, 0)
Comparaison des diagrammes VT isobare et adiabatique
Concept
Lorsque nous comparons la relation entre a température absolue ($T$) et le volume ($V$) dans le cas isotherme (où "iso" signifie égal et "barique" fait référence à la pression), nous obtenons l'équation suivante pour a température à l'état initial ($T_i$), a température à l'état final ($T_f$), le volume à l'état i ($V_i$) et le volume à l'état f ($V_f$) :
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Dans le cas adiabatique, cette équation doit être satisfaite avec le indice adiabatique ($\kappa$), ce qui nous conduit à l'équation suivante :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Si nous considérons $\kappa=1.4$, cela peut être observé graphiquement dans la représentation suivante :
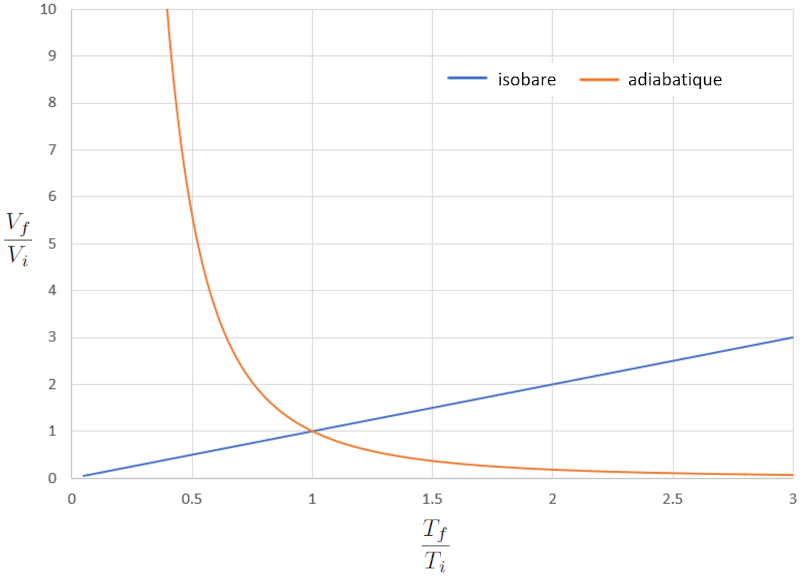
La grande différence de comportement d'un gaz dans un processus isobare par rapport à un processus adiabatique est que, dans le premier cas, si un système s'expand, la température augmente, tandis que dans le second cas, elle diminue.
ID:(11172, 0)
Formation des nuages par expansion adiabatique
Concept
Si de l'eau est placée dans une bouteille et que de l'air est pompé pour augmenter la pression, on obtient de l'air humide à haute pression. Lorsque la bouteille est ouverte à l'extérieur, l'air se dilate, ce qui entraîne une réduction de la température. Cela amène l'air à atteindre son point de saturation, ce qui entraîne la formation de vapeur d'eau et l'apparition d'un nuage.
ID:(11222, 0)
Comparaison des diagrammes pV isothermes et adiabatiques
Concept
Lorsque nous comparons la relation entre a pression ($p$) et le volume ($V$) dans le cas isotherme (iso = égal et thermique = température), nous avons la suivante équation pour a pression à l'état initial ($p_i$), a pression à l'état final ($p_f$), le volume à l'état i ($V_i$), et le volume à l'état f ($V_f$) :
| $ p_i V_i = p_f V_f $ |
Dans le cas adiabatique, cette équation doit être satisfaite avec le indice adiabatique ($\kappa$), ce qui nous conduit à l'équation suivante :
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Si nous considérons $\kappa=1,4$, cela peut être observé graphiquement de la manière suivante :
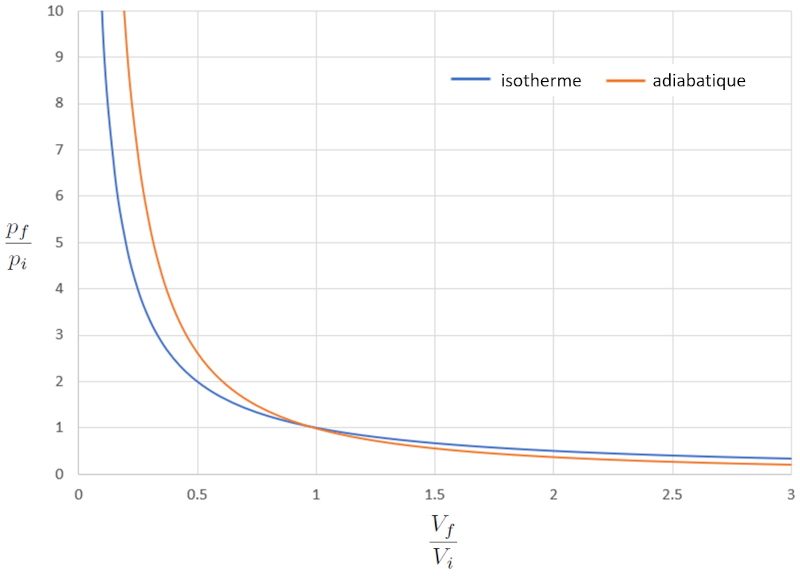
En d'autres termes, dans un processus de compression, si le processus est isotherme, la réponse est plus douce par rapport au cas adiabatique, car la pression augmente plus lentement. Dans un processus d'expansion, le comportement du gaz en mode adiabatique est plus doux.
ID:(11170, 0)
Casser un objet avec une compression adiabatique
Concept
Lorsqu'on frappe le haut d'une bouteille, celle-ci se déplace tandis que le liquide, en raison de son inertie, tend à rester en arrière. Cela crée un vide au fond de la bouteille, ce qui fait accélérer le liquide et finit par le faire frapper le fond de la bouteille, la brisant. Ce phénomène est connu sous le nom de "martelage de l'eau" (water hammer). La réaction adiabatique du matériau, due à la courte durée de l'impact, le rend plus rigide et contribue à l'effet de martelage de l'eau.
Cependant, dans le cas d'une boisson gazeuse, le liquide a tendance à céder aux bulles de gaz. Ces bulles permettent au liquide de se contracter plutôt que de frapper le fond de la bouteille, ce qui évite sa rupture. À la place, le liquide est expulsé à travers les bulles générées.
ID:(11223, 0)
Comparaison des diagrammes pT isochore et adiabatique
Concept
Lorsque nous comparons la relation entre a température absolue ($T$) et a pression ($p$) dans le cas isochore (où "iso" signifie égal et "chore" fait référence au volume), nous obtenons l'équation suivante pour a pression à l'état initial ($p_i$), a pression à l'état final ($p_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
Dans le cas adiabatique, cette équation doit être satisfaite avec le indice adiabatique ($\kappa$), ce qui nous conduit à l'équation suivante :
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Si nous considérons $\kappa=1.4$, cela peut être observé graphiquement dans la représentation suivante :
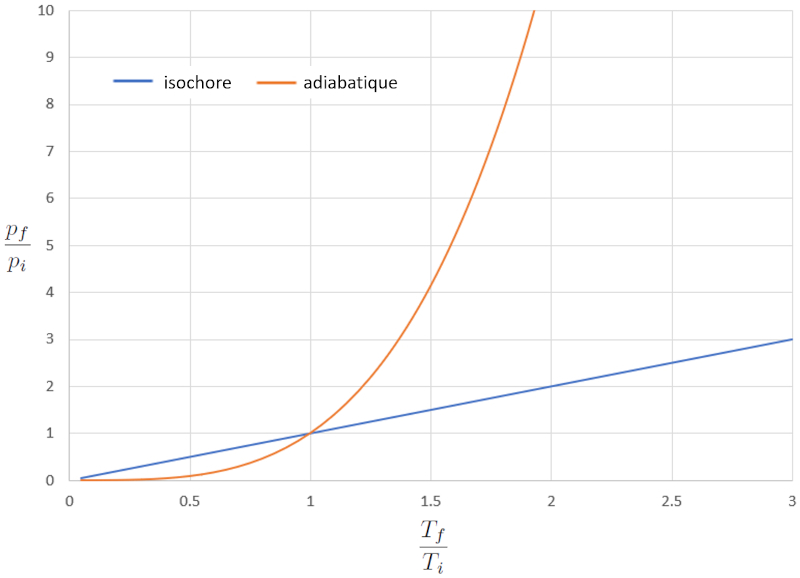
Dans ce cas, la différence significative se produit à des températures plus élevées, où la pression augmente de manière dramatique. En d'autres termes, si nous augmentons la pression de manière drastique dans le cas adiabatique, la température varie seulement légèrement, tandis que dans le cas normal, elle augmente de manière significative.
ID:(11171, 0)
Incinérer un objet avec une compression adiabatique
Concept
Si un objet est placé dans un récipient d'air dont la pression peut être augmentée de manière spectaculaire, en effectuant une compression adiabatique, il est possible d'élever la température au point où le matériau s'enflamme spontanément.
ID:(11221, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \delta Q =0$
dQ =0
$ p_i V_i = n_i R T_i $
p * V = n * R * T
$ p_f V_f = n_f R T_f $
p * V = n * R * T
$ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$
p_i * V_i ^ kappa = p_f * V_f ^ kappa
$ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$
p_i ^(1- kappa )* T_i ^ kappa = p_f ^(1- kappa )* T_f ^ kappa
$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$
T_i * V_i ^( kappa -1)= T_f * V_f ^( kappa -1)
ID:(15324, 0)
État adiabatique
Équation
Dans le cas adiabatique, le système n'a pas la possibilité de modifier le teneur en calories ($Q$), ce qui signifie que le différence de chaleur inexacte ($\delta Q$) doit être nul :
| $ \delta Q =0$ |
ID:(4860, 0)
Relation de cas adiabatique de la température et du volume
Équation
D'un état initial (i) avec le volume à l'état i ($V_i$) et a température à l'état initial ($T_i$) on passe à un état final (f) avec le volume à l'état f ($V_f$) et a température à l'état final ($T_f$) selon :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Dans le cas adiabatique, pour température absolue ($T$) et le volume ($V$) avec a constante du gaz universel ($R$), a masse molaire ($M_m$), ($$), a variation de température ($dT$) et a variation de volume ($dV$), nous avons l'équation suivante :
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
En introduisant le indice adiabatique ($\kappa$), cette équation peut être exprimée comme suit :
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Cela nous permet d'écrire l'équation comme suit :
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Si nous intégrons cette expression entre le volume à l'état i ($V_i$) et le volume à l'état f ($V_f$), ainsi qu'entre a température à l'état initial ($T_i$) et a température à l'état final ($T_f$), nous obtenons :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(4865, 0)
Relation de cas adiabatique de la pression et du volume
Équation
D'un état initial (i) avec a pression à l'état final ($p_f$) et le volume à l'état i ($V_i$) on passe à un état final (f) avec a pression à l'état final ($p_f$) et le volume à l'état f ($V_f$) selon :
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Avec les valeurs le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$) et le indice adiabatique ($\kappa$), la relation suivante est présentée :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
En utilisant l'équation des gaz avec les paramètres a pression ($p$), le volume ($V$), le nombre de taupes ($n$), a constante du gaz universel ($R$) et a température absolue ($T$), nous obtenons l'expression suivante :
| $ p V = n R T $ |
Cette équation décrit comment, dans un processus adiabatique variant d'une situation initiale à une situation finale en termes de a pression ($p$) et le volume ($V$), elle est reliée à A pression à l'état initial ($p_i$) et a pression à l'état final ($p_f$) de la manière suivante :
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(4867, 0)
Relation de cas adiabatique de la température et de la pression
Équation
D'un état initial (i) avec a pression à l'état initial ($p_i$) et a température à l'état initial ($T_i$) on passe à un état final (f) avec a pression à l'état final ($p_f$) et a température à l'état final ($T_f$) selon :
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Com os valores de le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$) e le indice adiabatique ($\kappa$), estabelece-se a seguinte relação:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Ao utilizar a equação dos gases com os parâmetros a pression ($p$), le volume ($V$), le nombre de taupes ($n$), a constante du gaz universel ($R$) e a température absolue ($T$), obtemos a seguinte expressão:
| $ p V = n R T $ |
Esta equação descreve como, em um processo adiabático que varia de uma situação inicial para uma final em termos de a pression ($p$) e a température absolue ($T$), ela se relaciona com a pression à l'état initial ($p_i$) e a pression à l'état final ($p_f$) da seguinte forma:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(4866, 0)
Loi spécifique sur les gaz (1)
Équation
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont liés par l'équation suivante :
| $ p_i V_i = n R T_i $ |
| $ p V = n R T $ |
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont liés par les lois physiques suivantes :
• Loi de Boyle
| $ p V = C_b $ |
• Loi de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Loi de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Loi d'Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Ces lois peuvent être exprimées de manière plus générale comme suit :
$\displaystyle\frac{pV}{nT}=cte$
Cette relation générale établit que le produit de la pression et du volume divisé par le nombre de moles et la température reste constant :
| $ p V = n R T $ |
où A constante du gaz universel ($R$) a une valeur de 8,314 J/K·mol.
ID:(3183, 1)
Loi spécifique sur les gaz (2)
Équation
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont liés par l'équation suivante :
| $ p_f V_f = n R T_f $ |
| $ p V = n R T $ |
A pression ($p$), le volume ($V$), a température absolue ($T$) et le nombre de taupes ($n$) sont liés par les lois physiques suivantes :
• Loi de Boyle
| $ p V = C_b $ |
• Loi de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Loi de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Loi d'Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Ces lois peuvent être exprimées de manière plus générale comme suit :
$\displaystyle\frac{pV}{nT}=cte$
Cette relation générale établit que le produit de la pression et du volume divisé par le nombre de moles et la température reste constant :
| $ p V = n R T $ |
où A constante du gaz universel ($R$) a une valeur de 8,314 J/K·mol.
ID:(3183, 2)