Adiabatic relations
Storyboard 
Adiabatic relations describe how a gas's properties change during an adiabatic process, where no heat is exchanged with the surroundings. For an ideal gas, the pressure and volume are related such that their product, raised to the power of the adiabatic index, remains constant. Similarly, the temperature and volume relationship follows that temperature, multiplied by volume raised to one minus the adiabatic index, is constant. The temperature and pressure relationship also follows a similar pattern, indicating that temperature and pressure changes are linked in a predictable way during adiabatic processes.
ID:(1481, 0)
Adiabatic process
Image 
When a gas expands rapidly, the water vapor molecules do not have enough time to exchange energy with the surroundings, so no heat is transferred, that is, the variation of heat ($\delta Q$) remains constant:
$\delta Q = 0$
The processes that are carried out under this condition are called adiabatic processes [1,2].
The expansion of the gas requires the system to do work or generate the differential inexact labour ($\delta W$). However, the energy needed for this cannot come from the internal energy ($U$), so it must be obtained from heat. As a result, the temperature of the system decreases, leading to a decrease in the variation of heat ($\delta Q$).
A typical example of this process is the formation of clouds. When air rises through convection, it expands, performs work, and cools down. The moisture in the air condenses, forming clouds.
Conversely, when work is done on the system, positive work the differential inexact labour ($\delta W$) is done. However, since the internal energy ($U$) cannot increase, the thermal energy in the variation of heat ($\delta Q$) increases, leading to an increase in the system's temperature.
A common example of this process is using a pump. If we try to inflate something rapidly, we do work on the system adiabatically, leading to an increase in ERROR:5202
![]() [1] "Réflexions sur la puissance motrice du feu" (Reflections on the Motive Power of Fire), Sadi Carnot, 1824
[1] "Réflexions sur la puissance motrice du feu" (Reflections on the Motive Power of Fire), Sadi Carnot, 1824
![]() [2] "Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen" (On the Moving Force of Heat and the Laws Which Can Be Deduced from It for the Theory of Heat Itself), Rudolf Clausius, Annalen der Physik und Chemie, 1850
[2] "Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen" (On the Moving Force of Heat and the Laws Which Can Be Deduced from It for the Theory of Heat Itself), Rudolf Clausius, Annalen der Physik und Chemie, 1850
ID:(41, 0)
Adiabatic case relationship of temperature and volume
Note 
In the adiabatic case, for ERROR:5177,0 and the volume ($V$) with the universal gas constant ($R_C$), the molar Mass ($M_m$), the specific heat of gases at constant volume ($c_V$), the temperature variation ($dT$), and the volume Variation ($\Delta V$), we have the following equation:
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R_C }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
By introducing the adiabatic index ($\kappa$), this equation can be expressed as:
| $ \kappa \equiv1+\displaystyle\frac{ R_C }{ M_m c_V }$ |
This allows us to write the equation as:
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
If we integrate this expression between the volume in state i ($V_i$) and the volume in state f ($V_f$), as well as between the temperature in initial state ($T_i$) and the temperature in final state ($T_f$), we obtain:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(15741, 0)
Adiabatic Pressure and Volume Case Relationship
Quote 
With the values the volume in state i ($V_i$), the volume in state f ($V_f$), the temperature in initial state ($T_i$), the temperature in final state ($T_f$), and the adiabatic index ($\kappa$), the following relationship is presented:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Using the gas equation with the parameters the pressure ($p$), the volume ($V$), the number of moles ($n$), the universal gas constant ($R_C$), and the absolute temperature ($T$), we obtain the following expression:
| $ p V = n R_C T $ |
This equation describes how, in an adiabatic process that varies from an initial situation to a final one in terms of the pressure ($p$) and the volume ($V$), it is related to the pressure in initial state ($p_i$) and the pressure in final state ($p_f$) as follows:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(15742, 0)
Adiabatic case relationship of temperature and pressure
Exercise 
With the values of the volume in state i ($V_i$), the volume in state f ($V_f$), the temperature in initial state ($T_i$), the temperature in final state ($T_f$), and the adiabatic index ($\kappa$), the following relationship is established:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
By utilizing the gas equation with the parameters the pressure ($p$), the volume ($V$), the number of moles ($n$), the universal gas constant ($R_C$), and the absolute temperature ($T$), we derive the following expression:
| $ p V = n R_C T $ |
This equation describes how, in an adiabatic process varying from an initial situation to a final one in terms of the pressure ($p$) and the absolute temperature ($T$), it relates to the pressure in initial state ($p_i$) and the pressure in final state ($p_f$) as follows:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(15743, 0)
Comparison of isobaric and adiabatic VT diagram
Equation 
When we compare the relationship between the absolute temperature ($T$) and the volume ($V$) in the isothermal case (where "iso" means equal and "baric" refers to pressure), we obtain the following equation for the temperature in initial state ($T_i$), the temperature in final state ($T_f$), the volume in state i ($V_i$), and the volume in state f ($V_f$):
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
In the adiabatic case, this equation must be satisfied with the adiabatic index ($\kappa$), leading us to the following equation:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
If we consider $\kappa=1.4$, this can be observed graphically in the following representation:
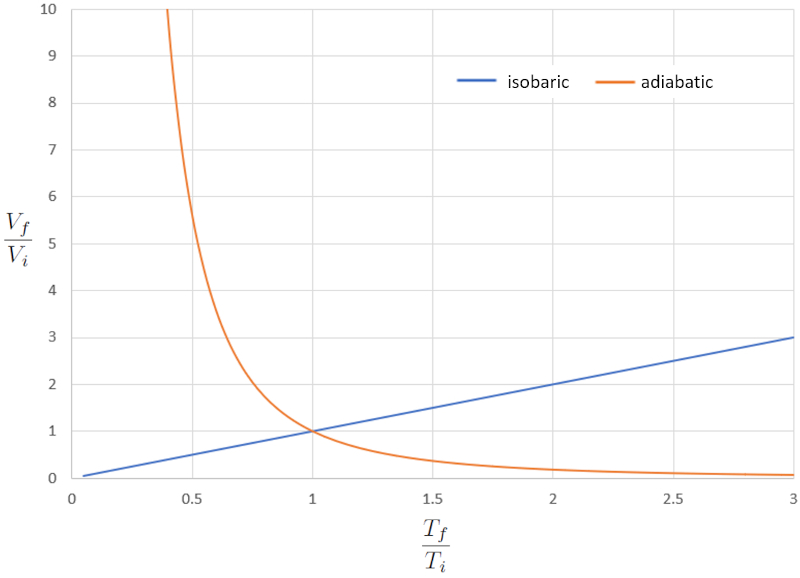
The significant difference in the behavior of a gas in an isobaric process compared to an adiabatic process is that in the first case, if a system expands, the temperature increases, whereas in the second case, it decreases.
ID:(11172, 0)
Cloud formation by adiabatic expansion
Script 
If water is placed in a bottle and air is pumped to increase the pressure, high-pressure moist air is obtained. When the bottle is opened to the outside, the air expands, causing a reduction in temperature. This leads the air to reach its saturation point, resulting in the formation of water vapor and the appearance of a cloud.
Cloud in a Bottle - Sick Science! #076 (https://www.youtube.com/watch?v=LHjDT9pYxRA)
ID:(11222, 0)
Comparison of isothermal and adiabatic pV diagram
Variable 
When we compare the relationship between the pressure ($p$) and the volume ($V$) in the isothermal case (iso = equal and thermal = temperature), we have for the pressure in initial state ($p_i$), the pressure in final state ($p_f$), the volume in state i ($V_i$), and the volume in state f ($V_f$) the following equation:
| $ p_i V_i = p_f V_f $ |
In the adiabatic case, this equation must be satisfied with the adiabatic index ($\kappa$), leading to the following equation:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
If we consider $\kappa=1.4$, this can be observed graphically as follows:
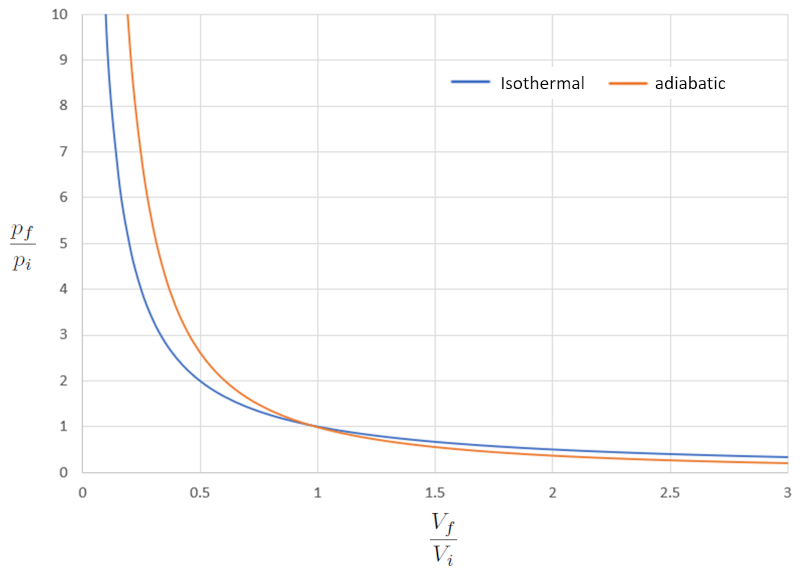
In other words, in a compression process, if the process is isothermal, the response is softer compared to the adiabatic case, as the pressure increases more slowly. In an expansion process, the gas behaves more softly in an adiabatic manner.
ID:(11170, 0)
Breaking an object with adiabatic compression
Audio 
When a bottle is struck on its top, the bottle moves while the liquid, due to inertia, tends to stay behind. This creates a vacuum at the bottom of the bottle, causing the liquid to accelerate and eventually strike the bottom, resulting in the bottle breaking. This phenomenon is known as water hammer. The short duration of the impact leads to an adiabatic reaction of the material, making it stiffer and contributing to the water hammer effect.
However, in the case of a carbonated beverage, the liquid tends to give way to the gas bubbles. These bubbles allow the liquid to contract instead of striking the bottom of the bottle, preventing its rupture. Instead, the liquid is expelled through the generated bubbles.
Extracted from WATER HAMMER (18,000FPS) | Why Does SODA Not Break the Bottle? (https://www.youtube.com/watch?v=tlRikG7FOdw)
ID:(11223, 0)
Comparison of isocoric and adiabatic pT diagram
Video 
When we compare the relationship between the absolute temperature ($T$) and the pressure ($p$) in the isochoric case (where "iso" signifies equal and "choric" refers to volume), we obtain the following equation for the pressure in initial state ($p_i$), the pressure in final state ($p_f$), the temperature in initial state ($T_i$), and the temperature in final state ($T_f$):
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
In the adiabatic case, this equation must be satisfied with the adiabatic index ($\kappa$), which leads us to the following equation:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
If we consider $\kappa=1.4$, this can be observed graphically in the following representation:
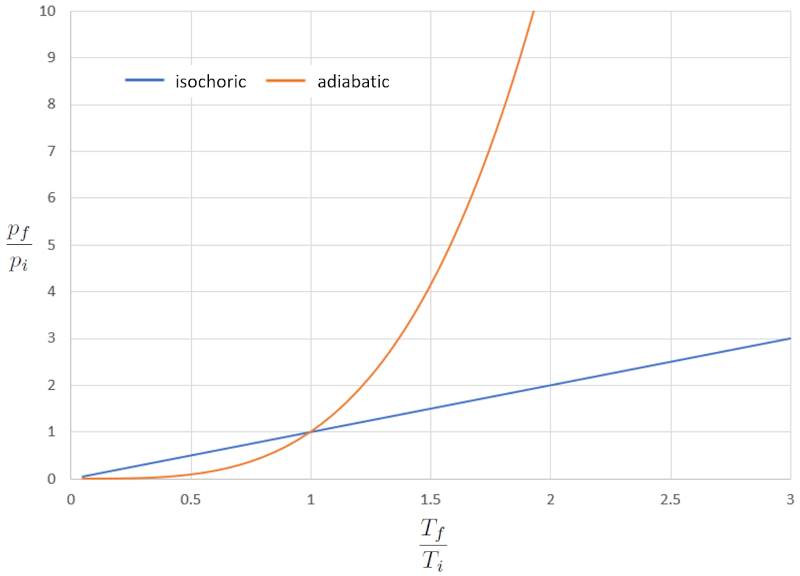
In this case, the significant difference arises at higher temperatures, where the pressure increases dramatically. In other words, if we increase the pressure dramatically in the adiabatic case, the temperature varies only slightly, whereas in the normal case, it increases significantly.
ID:(11171, 0)
Incinerate an object with adiabatic compression
Unit 
If an object is placed in a container of air that can be dramatically pressurized, by performing an adiabatic compression, the temperature can be raised to the point where the material spontaneously ignites.
Fire Syringe Demo (https://www.youtube.com/watch?v=OEwlwYqPIAw)
ID:(11221, 0)
