Usuario:
Relaciones adiabáticas
Storyboard 
Las relaciones adiabáticas describen cómo cambian las propiedades de un gas durante un proceso adiabático, en el cual no se intercambia calor con el entorno. Para un gas ideal, la presión y el volumen están relacionados de tal manera que su producto, elevado a la potencia del índice adiabático, permanece constante. De manera similar, la relación entre la temperatura y el volumen sigue que la temperatura, multiplicada por el volumen elevado a uno menos el índice adiabático, es constante. La relación entre temperatura y presión también sigue un patrón similar, indicando que los cambios de temperatura y presión están vinculados de manera predecible durante los procesos adiabáticos.
ID:(1481, 0)
Proceso adiábatico
Concepto
Cuando un gas se expande rápidamente, las moléculas de vapor de agua no tienen tiempo suficiente para intercambiar energía con el entorno, por lo que no se transfere calor, es decir, la variación de calor ($\delta Q$) se mantiene constante:
$\delta Q = 0$
Los procesos que se realizan bajo esta condición se denominan procesos adiabaticos [1,2].
La expansión del gas requiere que el sistema realice trabajo o genere el diferencial inexacto del trabajo ($\delta W$). Sin embargo, la energía necesaria para esto no puede provenir de la energía interna ($U$), por lo que se debe obtener del calor. Como resultado, la temperatura del sistema disminuye, lo que se refleja en una reducción de la variación de calor ($\delta Q$).
Un ejemplo típico de este proceso es la formación de nubes. Cuando el aire asciende por convección, se expande y realiza trabajo, lo que provoca un enfriamiento. La humedad presente en el aire se condensa, formando nubes.
Por otro lado, cuando se realiza trabajo sobre el sistema, se realiza un trabajo positivo el diferencial inexacto del trabajo ($\delta W$), pero como la energía interna ($U$) no puede aumentar, la energía térmica en la variación de calor ($\delta Q$) aumenta, lo que significa un aumento en la temperatura del sistema.
Un ejemplo común de este proceso es el funcionamiento de una bomba. Si intentamos inflar algo rápidamente, realizamos trabajo sobre el sistema de manera adiabática, lo que resulta en un aumento de la variación de calor ($\delta Q$) y, por lo tanto, en un aumento de la temperatura del sistema.
[1] "Réflexions sur la puissance motrice du feu" (Reflexiones sobre la fuerza motriz del fuego), Sadi Carnot, 1824
[2] "Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen" (Sobre la fuerza móvil del calor y las leyes que de ella se pueden derivar para la teoría del calor misma), Rudolf Clausius, Annalen der Physik und Chemie, 1850
ID:(41, 0)
Relación caso adiabático de temperatura y volumen
Concepto
En el caso adiabático, para temperatura absoluta ($T$) y el volumen ($V$) con la constante universal de los gases ($R$), la masa molar ($M_m$), el calor específico de gases a volumen constante ($c_V$), la variación de la temperatura ($dT$) y la variación del volumen ($dV$), se tiene la siguiente ecuación:
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
Al introducir el indice adiabático ($\kappa$), esta ecuación se puede expresar como:
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Lo que nos permite escribir la ecuación como:
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Si integramos esta expresión entre el volumen en estado i ($V_i$) y el volumen en estado f ($V_f$), así como entre la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$), obtenemos:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(15741, 0)
Relación caso adiabático de presión y volumen
Concepto
Con los valores el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$), se presenta la siguiente relación:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Utilizando la ecuación de los gases con los parámetros la presión ($p$), el volumen ($V$), el número de moles ($n$), la constante universal de los gases ($R$) y la temperatura absoluta ($T$), obtenemos la siguiente expresión:
| $ p V = n R T $ |
Esta ecuación describe cómo, en un proceso adiabático que varía desde una situación inicial hasta una final en términos de la presión ($p$) y el volumen ($V$), se relaciona con la presión en estado inicial ($p_i$) y la presión en estado final ($p_f$) de la siguiente manera:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(15742, 0)
Relación caso adiabático de temperatura y presión
Concepto
Con los valores de el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$), y el indice adiabático ($\kappa$), se establece la siguiente relación:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Al emplear la ecuación de los gases con los parámetros la presión ($p$), el volumen ($V$), el número de moles ($n$), la constante universal de los gases ($R$) y la temperatura absoluta ($T$), obtenemos la siguiente expresión:
| $ p V = n R T $ |
Esta ecuación describe cómo, en un proceso adiabático que varía desde una situación inicial hasta una final en términos de la presión ($p$) y la temperatura absoluta ($T$), se relaciona con la presión en estado inicial ($p_i$) y la presión en estado final ($p_f$) de la siguiente manera:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
.
ID:(15743, 0)
Comparación diagrama VT isobárico y adiabático
Concepto
Cuando comparamos la relación entre la temperatura absoluta ($T$) y el volumen ($V$) en el caso isotérmico (donde "iso" significa igual y "barico" se refiere a la presión), obtenemos la siguiente ecuación para la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$), el volumen en estado i ($V_i$) y el volumen en estado f ($V_f$):
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
En el caso adiabático, esta ecuación debe satisfacerse con el indice adiabático ($\kappa$), lo que nos lleva a la siguiente ecuación:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Si consideramos $\kappa=1,4$, esto se puede observar gráficamente en la siguiente representación:
La gran diferencia en el comportamiento de un gas en un proceso isobárico en comparación con un proceso adiabático es que, en el primer caso, si un sistema se expande, la temperatura aumenta, mientras que en el segundo caso, disminuye.
ID:(11172, 0)
Formación de nubes por expansión adiabática
Concepto
Si se coloca agua en una botella y se bombea aire para aumentar la presión, se obtiene aire con alta humedad a presión elevada. Si se abre la botella al exterior, el aire se expande, lo que provoca una reducción de la temperatura y lleva al aire a su punto de saturación, dando lugar a la formación de vapor de agua y la aparición de una nube.
Cloud in a Bottle - Sick Science! #076 (https://www.youtube.com/watch?v=LHjDT9pYxRA)
ID:(11222, 0)
Comparación diagrama pV isotérmico y adiabático
Concepto
Cuando comparamos la relación entre la presión ($p$) y el volumen ($V$) en el caso isotérmico (iso = igual y térmico = temperatura), tenemos para la presión en estado inicial ($p_i$), la presión en estado final ($p_f$), el volumen en estado i ($V_i$) y el volumen en estado f ($V_f$) la siguiente ecuación:
| $ p_i V_i = p_f V_f $ |
En el caso adiabático, esta ecuación debe satisfacerse con el indice adiabático ($\kappa$), lo que nos lleva a la siguiente ecuación:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Si consideramos $\kappa=1.4$, esto se puede observar de manera gráfica en la siguiente representación:
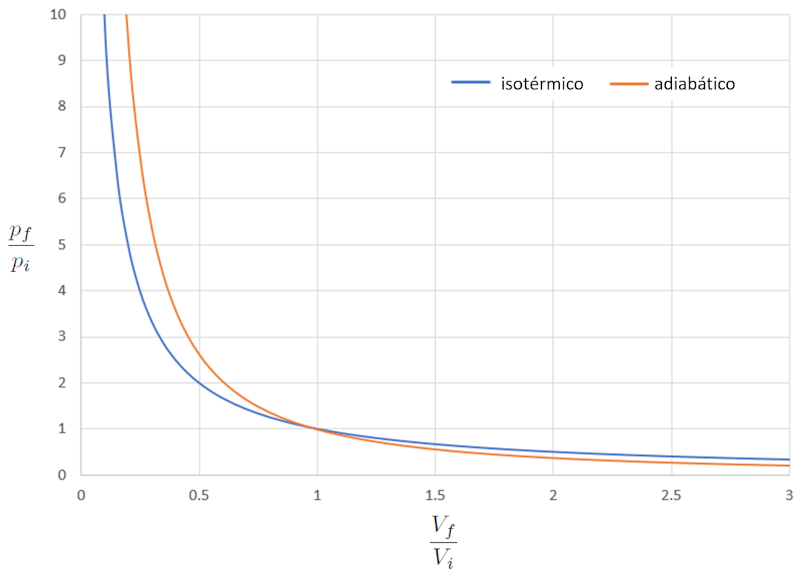
En otras palabras, en un proceso de compresión, si el proceso es isotérmico, la respuesta es más suave en comparación con el caso adiabático, ya que la presión aumenta más lentamente. En un proceso de expansión, el comportamiento del gas en modo adiabático es más suave.
ID:(11170, 0)
Romper un objeto con compresión adiabática
Concepto
Cuando se golpea la parte superior de una botella, la botella se desplaza mientras que el líquido, debido a la inercia, tiende a quedarse atrás. Esto crea un vacío en el fondo de la botella, lo que provoca que el líquido se acelere y eventualmente golpee el fondo de la botella, causando su ruptura. Este fenómeno se conoce como el "martillo de agua" (water hammer). La reacción adiabática del material, debido al corto tiempo del impacto, lo hace más rígido, lo que contribuye a este efecto.
Sin embargo, en el caso de una bebida gaseosa, el líquido tiende a ceder en las burbujas de gas. Estas burbujas permiten que el líquido se contraiga en lugar de golpear el fondo de la botella, lo que evita su ruptura. En cambio, el líquido es expulsado a través de las burbujas generadas.
Extraído de WATER HAMMER (18,000FPS) | Why Does SODA Not Break the Bottle? (https://www.youtube.com/watch?v=tlRikG7FOdw)
ID:(11223, 0)
Comparación diagrama pT isocórico y adiabático
Concepto
Cuando comparamos la relación entre la temperatura absoluta ($T$) y la presión ($p$) en el caso isocórico (donde "iso" significa igual y "córico" se refiere al volumen), obtenemos la siguiente ecuación para la presión en estado inicial ($p_i$), la presión en estado final ($p_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):
| $\displaystyle\frac{ p_i }{ T_i }=\displaystyle\frac{ p_f }{ T_f }$ |
En el caso adiabático, esta ecuación debe cumplirse con el indice adiabático ($\kappa$), lo que nos conduce a la siguiente expresión:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Si consideramos $\kappa=1.4$, esto se puede observar de forma gráfica en la siguiente representación:
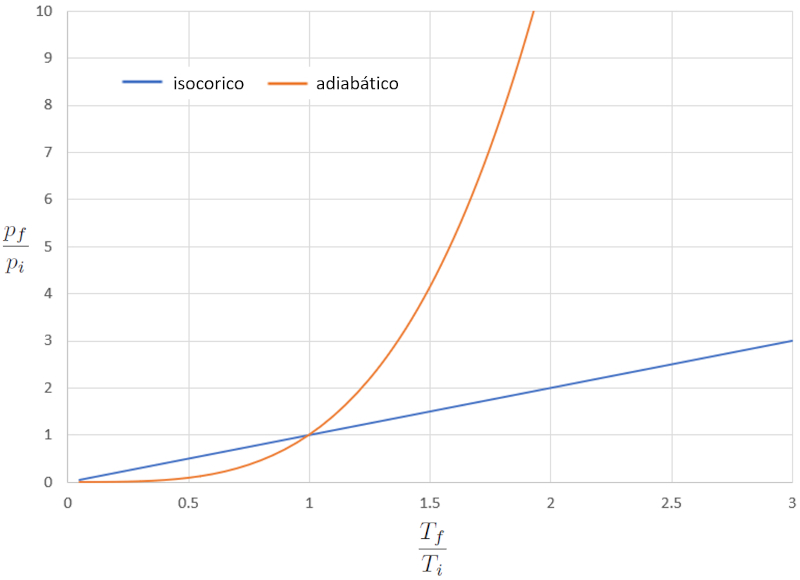
En este caso, la diferencia más significativa se presenta a temperaturas elevadas, donde la presión aumenta de forma drástica. En otras palabras, si aumentamos drásticamente la presión en el caso adiabático, la temperatura variará solo ligeramente, mientras que en el caso normal, la variación será más pronunciada.
ID:(11171, 0)
Incinerar un objeto con compresión adiabática
Concepto
Si se coloca un objeto en un contenedor de aire al que se le puede aumentar la presión de manera dramática, al realizar una compresión adiabática, se puede elevar la temperatura hasta el punto en que el material se incinera de forma espontánea.
Fire Syringe Demo (https://www.youtube.com/watch?v=OEwlwYqPIAw)
ID:(11221, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \delta Q =0$
dQ =0
$ p_i V_i = n_i R T_i $
p * V = n * R * T
$ p_f V_f = n_f R T_f $
p * V = n * R * T
$ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$
p_i * V_i ^ kappa = p_f * V_f ^ kappa
$ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$
p_i ^(1- kappa )* T_i ^ kappa = p_f ^(1- kappa )* T_f ^ kappa
$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$
T_i * V_i ^( kappa -1)= T_f * V_f ^( kappa -1)
ID:(15324, 0)
Condición adiabatica
Ecuación
En el caso adiabático, el sistema no tiene la capacidad de cambiar el contenido calórico ($Q$), es decir, el diferencial inexacto del calor ($\delta Q$) debe ser nulo:
| $ \delta Q =0$ |
ID:(4860, 0)
Relación caso adiabático de temperatura y volumen
Ecuación
De un estado inicial (i) con el volumen en estado i ($V_i$) y la temperatura en estado inicial ($T_i$) pasa a un estado final (f) con el volumen en estado f ($V_f$) y la temperatura en estado final ($T_f$) con el indice adiabático ($\kappa$) según:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
En el caso adiabático, para temperatura absoluta ($T$) y el volumen ($V$) con la constante universal de los gases ($R$), la masa molar ($M_m$), el calor especifico a presión constante ($c_p$), la variación de la temperatura ($dT$) y la variación del volumen ($dV$), se tiene la siguiente ecuación:
| $\displaystyle\frac{ dT }{ T }=-\displaystyle\frac{ R }{ M_m c_V }\displaystyle\frac{ dV }{ V }$ |
Al introducir el indice adiabático ($\kappa$), esta ecuación se puede expresar como:
| $ \kappa \equiv1+\displaystyle\frac{ R }{ M_m c_V }$ |
Lo que nos permite escribir la ecuación como:
$\displaystyle\frac{dT}{T}=-(\kappa - 1)\displaystyle\frac{dV}{V}$
Si integramos esta expresión entre el volumen en estado i ($V_i$) y el volumen en estado f ($V_f$), así como entre la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$), obtenemos:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
ID:(4865, 0)
Relación caso adiabático de presión y volumen
Ecuación
De un estado inicial (i) con la presión en estado final ($p_f$) y el volumen en estado i ($V_i$) pasa a un estado final (f) con la presión en estado final ($p_f$) y el volumen en estado f ($V_f$) con el indice adiabático ($\kappa$) según:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
Con los valores el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$) y el indice adiabático ($\kappa$), se presenta la siguiente relación:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Utilizando la ecuación de los gases con los parámetros la presión ($p$), el volumen ($V$), el número de moles ($n$), la constante universal de los gases ($R$) y la temperatura absoluta ($T$), obtenemos la siguiente expresión:
| $ p V = n R T $ |
Esta ecuación describe cómo, en un proceso adiabático que varía desde una situación inicial hasta una final en términos de la presión ($p$) y el volumen ($V$), se relaciona con la presión en estado inicial ($p_i$) y la presión en estado final ($p_f$) de la siguiente manera:
| $ p_i V_i ^{ \kappa }= p_f V_f ^{ \kappa }$ |
ID:(4867, 0)
Relación caso adiabático de temperatura y presión
Ecuación
De un estado inicial (i) con la presión en estado inicial ($p_i$) y la temperatura en estado inicial ($T_i$) pasa a un estado final (f) con la presión en estado final ($p_f$) y la temperatura en estado final ($T_f$) con el indice adiabático ($\kappa$) según:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
Con los valores de el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$), la temperatura en estado final ($T_f$), y el indice adiabático ($\kappa$), se establece la siguiente relación:
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Al emplear la ecuación de los gases con los parámetros la presión ($p$), el volumen ($V$), el número de moles ($n$), la constante universal de los gases ($R$) y la temperatura absoluta ($T$), obtenemos la siguiente expresión:
| $ p V = n R T $ |
Esta ecuación describe cómo, en un proceso adiabático que varía desde una situación inicial hasta una final en términos de la presión ($p$) y la temperatura absoluta ($T$), se relaciona con la presión en estado inicial ($p_i$) y la presión en estado final ($p_f$) de la siguiente manera:
| $ p_i ^{1- \kappa } T_i ^{ \kappa }= p_f ^{1- \kappa } T_f ^{ \kappa }$ |
ID:(4866, 0)
Ley general de los gases (1)
Ecuación
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$), y el número de moles ($n$) están relacionados por la siguiente ecuación:
| $ p_i V_i = n_i R T_i $ |
| $ p V = n R T $ |
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) están vinculados a través de las siguientes leyes físicas:
• La ley de Boyle
| $ p V = C_b $ |
• La ley de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• La ley de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• La ley de Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Estas leyes pueden ser expresadas de manera más general como:
$\displaystyle\frac{pV}{nT}=cte$
Esta relación general establece que el producto de la presión y el volumen dividido por el número de moles y la temperatura se mantiene constante:
| $ p V = n R T $ |
donde la constante universal de los gases ($R$) tiene el valor de 8.314 J/K·mol.
ID:(3183, 1)
Ley general de los gases (2)
Ecuación
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$), y el número de moles ($n$) están relacionados por la siguiente ecuación:
| $ p_f V_f = n_f R T_f $ |
| $ p V = n R T $ |
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) están vinculados a través de las siguientes leyes físicas:
• La ley de Boyle
| $ p V = C_b $ |
• La ley de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• La ley de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• La ley de Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Estas leyes pueden ser expresadas de manera más general como:
$\displaystyle\frac{pV}{nT}=cte$
Esta relación general establece que el producto de la presión y el volumen dividido por el número de moles y la temperatura se mantiene constante:
| $ p V = n R T $ |
donde la constante universal de los gases ($R$) tiene el valor de 8.314 J/K·mol.
ID:(3183, 2)