Usuario:


Elementos ópticos
Storyboard

>Modelo

ID:(1667, 0)


Geometría de los haces en un lente biconvexo
Imagen

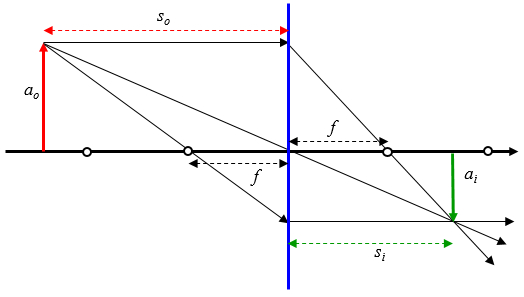
En el caso de un lente biconvexo un haz que alcanza el lente

- en forma paralela al eje óptico se refracta por el foco
- vía el foco se refracta en forma paralela al eje óptico
- vía el origen del eje óptico continua en forma rectilínea

lo que para el caso de un objeto a una distancia mayor que el foto corresponde a:

ID:(1856, 0)


Similitud tamaños y posiciones
Imagen

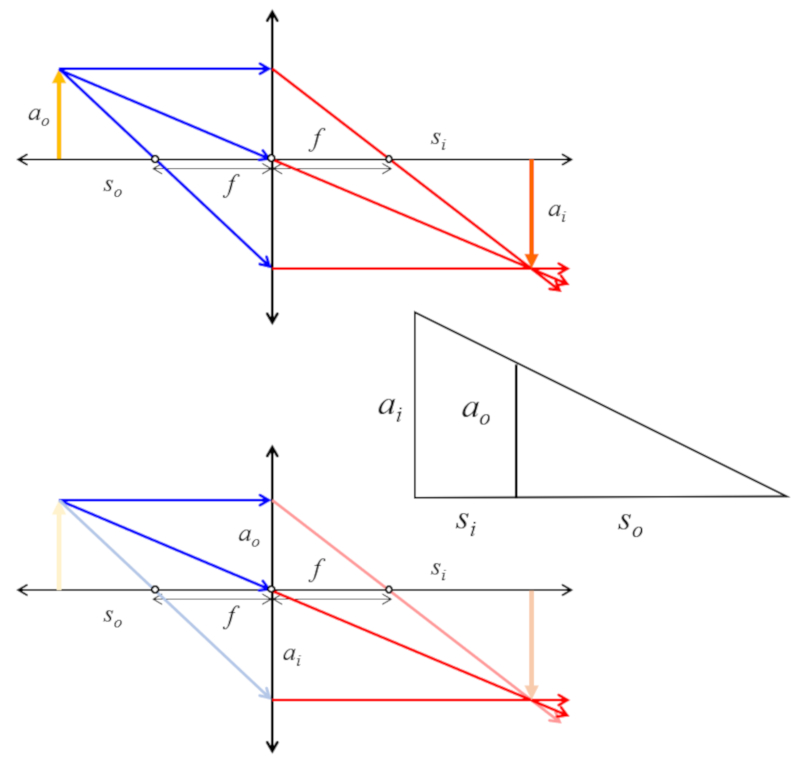
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones

ID:(12697, 0)


Similitud tamaños, posición de objeto y foco
Imagen

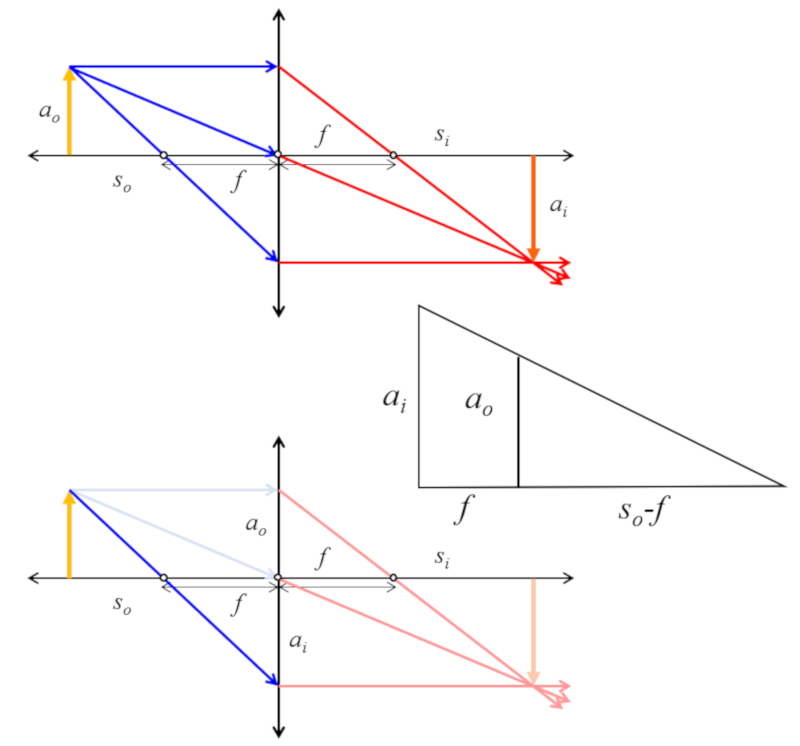
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:

ID:(12698, 0)


Posición de la imagen
Imagen

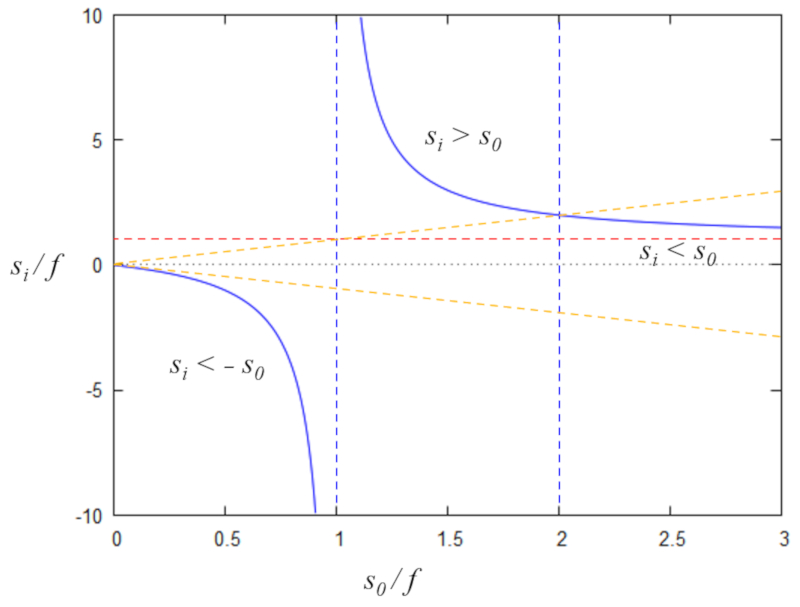
Como la relación entre el foco, posición del objeto y posición de la imagen esta dada por\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\ny se introduce las variables\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{s_i}{f}$

\\n\\nse puede escribir la relación\\n\\n

$y=\displaystyle\frac{x}{x-1}$



que se grafica como

ID:(12699, 0)


Tamaño de la imagen
Imagen

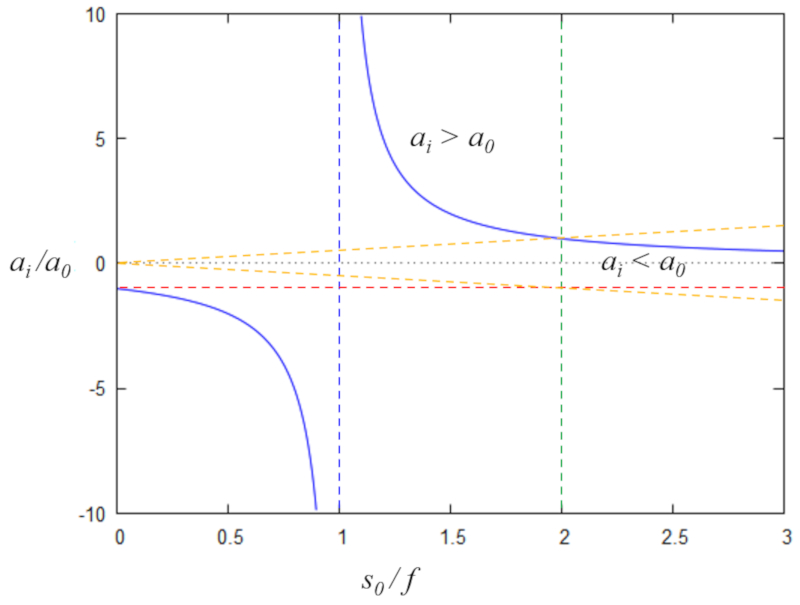
Como la relación de los tamaño de la imagen se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{s_i}{s_o}$

\\n\\nCon la relación entre las posiciones\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\nla relación de tamaños se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{1}{1-s_o/f}$

\\n\\npor lo que con\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{a_i}{a_o}$

\\n\\nse puede escribir la relación\\n\\n

$y=\displaystyle\frac{1}{x-1}$



que se grafica como

ID:(12700, 0)


Elementos ópticos
Modelo

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$s_{lc}$
s_lc
Distancia de la imagen del lente cóncavo
m
$s_o$
s_o
Distancia del objeto al lente cóncavo
m
$f_{lc}$
f_lc
Foco del lente cóncavo
m
$a_{lc}$
a_lc
Tamaño de la imagen en un lente cóncavo
m
$a_o$
a_o
Tamaño del objeto
m

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Una relaci n se puede armar con los tri ngulos del lado del objeto. En este caso la similitud nos permite escribir que el tama o del objeto a_o es a la distancia del objeto s_o al foco f es como el tama o de la imagen a_i es a la distancia del foco f:\\n\\n

$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$



Con la relaci n de similitud de los tri ngulos

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$



se puede mostrar que se cumple:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

(ID 3347)

Ejemplos

En el caso de un lente biconvexo un haz que alcanza el lente

- en forma paralela al eje ptico se refracta por el foco
- v a el foco se refracta en forma paralela al eje ptico
- v a el origen del eje ptico continua en forma rectil nea

lo que para el caso de un objeto a una distancia mayor que el foto corresponde a:

(ID 1856)

Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os con posiciones

(ID 12697)

Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os, posici n del objeto y foco:

(ID 12698)

Como la relaci n entre el foco, posici n del objeto y posici n de la imagen esta dada por\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\ny se introduce las variables\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{s_i}{f}$

\\n\\nse puede escribir la relaci n\\n\\n

$y=\displaystyle\frac{x}{x-1}$



que se grafica como

(ID 12699)

Como la relaci n de los tama o de la imagen se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{s_i}{s_o}$

\\n\\nCon la relaci n entre las posiciones\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\nla relaci n de tama os se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{1}{1-s_o/f}$

\\n\\npor lo que con\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{a_i}{a_o}$

\\n\\nse puede escribir la relaci n\\n\\n

$y=\displaystyle\frac{1}{x-1}$



que se grafica como

(ID 12700)

ID:(1667, 0)