Storyboard

En el caso de un espejo plano la luz se refleja en un angulo idéntico al con que incidió.

En general la luz no tiene la información de que se ha reflejado con lo que el ojo asume que la luz es originada 'detrás' del espejo.

>Modelo

ID:(1263, 0)

Imagen

>Top

Aplicando el principio de Huygens se muestra que un haz que incide sobre una superficie se refleja bajo un angulo igual al de incidencia:

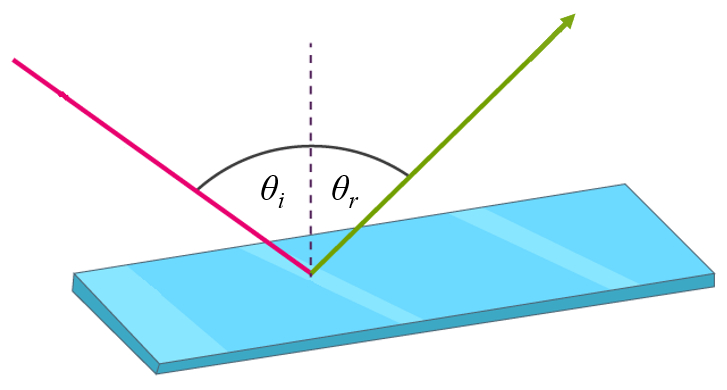
ID:(12758, 0)

Ecuación

>Top, >Modelo

Para la luz reflejada el angulo del haz respecto de la normal \theta_i es igual al angulo de reflexión \theta_r:

$ \theta_i = \theta_r $

Condiciones

Variables

$\theta_i$

Ángulo de Incidencia

$rad$

5096

$\theta_r$

Ángulo de Reflexión

$rad$

5097

Relación

ID:(3262, 0)

Imagen

>Top

Un espejo parece una ventana a otra habitación. El efecto es creado por la luz reflejada que el ojo asume no se reflejo si no que proviene de un objeto detrás del espejo.

ID:(9777, 0)

Ecuación

>Top, >Modelo

Para el calculo de los ángulos en el caso de que los haces se reflejan en un espejo es útil poder calcular el angulo complementario al de incidencia. Por ello se tiene que

$ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $

Condiciones

Variables

$\theta_{ic}$

Angulo complementario del angulo de incidencia

$rad$

8426

$\theta_i$

Ángulo de Incidencia

$rad$

5096

$\pi$

Pi

3.1415927

$rad$

5057

Relación

Desarrollo

Como la suma de los ángulos internos en un triangulo es

$ \pi = \alpha + \beta + \gamma $

se tiene que en un rectángulo, en el que uno de los ángulos es \pi/2 se tiene que

$ \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i $

ID:(10928, 0)

Ecuación

>Top, >Modelo

Para el calculo de los ángulos en el caso de que los haces se reflejan en un espejo es útil poder calcular el angulo complementario al de reflexión. Por ello se tiene que

$ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $

Condiciones

Variables

$\theta_{rc}$

Angulo complementario del angulo de reflección

$rad$

8423

$\theta_r$

Ángulo de Reflexión

$rad$

5097

$\pi$

Pi

3.1415927

$rad$

5057

Relación

Desarrollo

Como la suma de los ángulos internos en un triangulo es

$ \pi = \alpha + \beta + \gamma $

se tiene que en un rectángulo, en el que uno de los ángulos es \pi/2 se tiene que

$ \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r $

ID:(10925, 0)

Ecuación

>Top, >Modelo

$ \pi = \alpha + \beta + \gamma $

Condiciones

Variables

$\alpha$

Angulo complementario del angulo de incidencia

$rad$

9946

$\beta$

Angulo complementario del angulo de reflección

$rad$

9945

$\gamma$

Angulo entre ambos espejos

$rad$

8424

$\pi$

Pi

3.1415927

$rad$

5057

Relación

ID:(10926, 0)

Imagen

>Top

En caso de dos espejos con una esquina

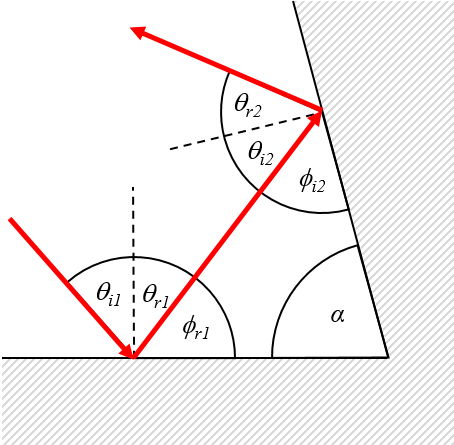
se pueden calcular los ángulos con la relación de reflexión

el calculo del complemento del angulo incidente

el calculo del complemento del angulo de reflección

y la relación entre los ángulos de un triangulo

ID:(12666, 0)

Ecuación

>Top, >Modelo

El angulo de incidencia \theta_i, y con ello el de reflexión \theta_r, se asocia al camino recorrido paralelo al espejo h/2 y la distancia a este d mediante:

$ \tan \theta_i =\displaystyle\frac{ h }{2 d }$

Condiciones

Variables

$\theta_i$

Ángulo de Incidencia

$rad$

5096

$d$

Distancia al espejo

$m$

7920

$h$

Distancia que haz avanza paralelo al espejo

$m$

7921

Relación

ID:(9779, 0)

Imagen

>Top

Del análisis mediante el principio de Huygens se concluye que los ángulos de incidencia y reflexión son iguales:

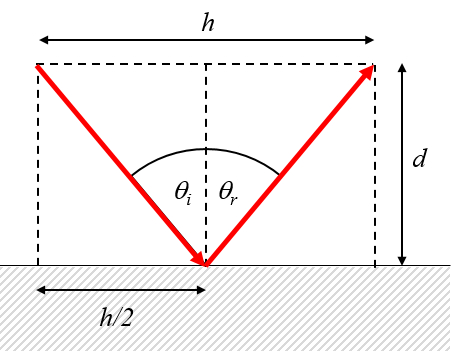
ID:(12665, 0)

0

Video

Video: Espejo Plano