User:


Optical elements
Storyboard

>Model

ID:(1667, 0)


Geometry of the Beams on a Lens
Definition

In the case of a biconvex lens a beam that reaches the lens

- parallel to the optical axis is refracted by the focus
- via the focus is refracted parallel to the optical axis
- via the origin of the continuous optical axis in a straight line

what in the case of an object at a distance greater than the photo corresponds to:

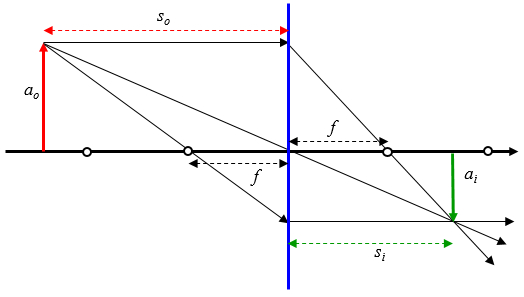
ID:(1856, 0)


Similitud tamaños y posiciones
Image

Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones

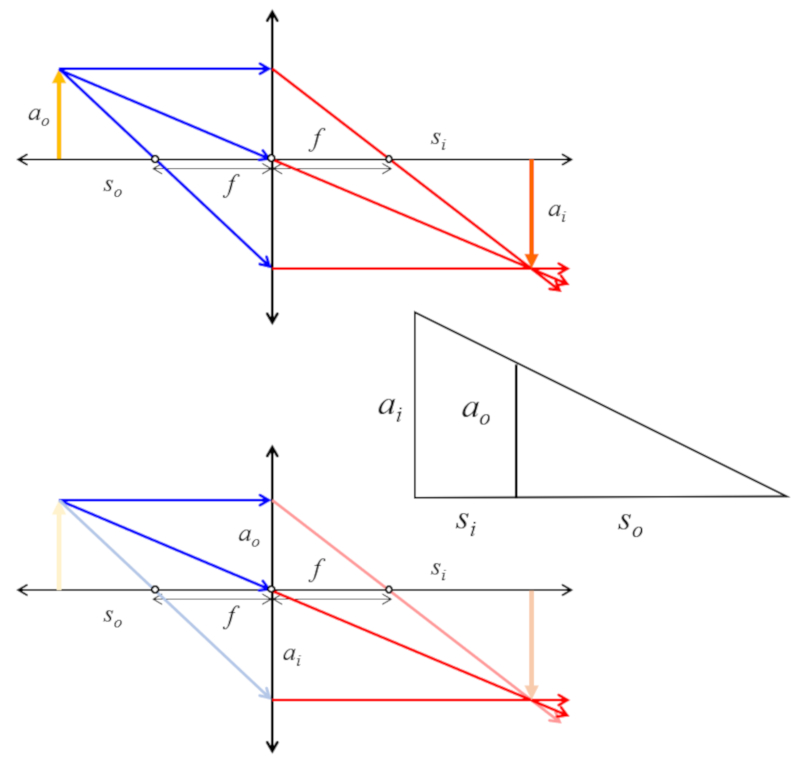
ID:(12697, 0)


Similitud tamaños, posición de objeto y foco
Note

Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:

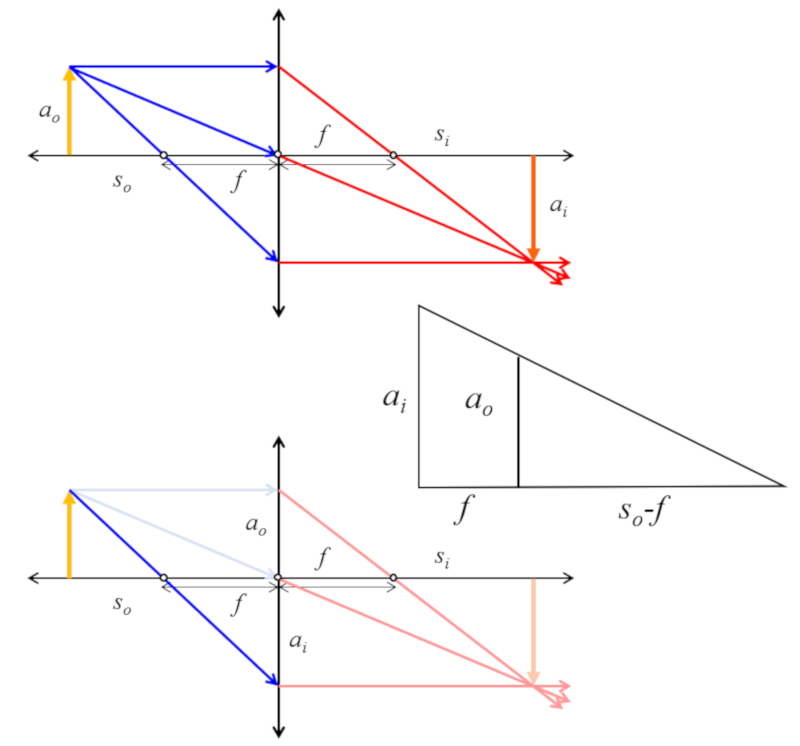
ID:(12698, 0)


Posición de la imagen
Quote

Como la relación entre el foco, posición del objeto y posición de la imagen esta dada por\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\ny se introduce las variables\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{s_i}{f}$

\\n\\nse puede escribir la relación\\n\\n

$y=\displaystyle\frac{x}{x-1}$



que se grafica como

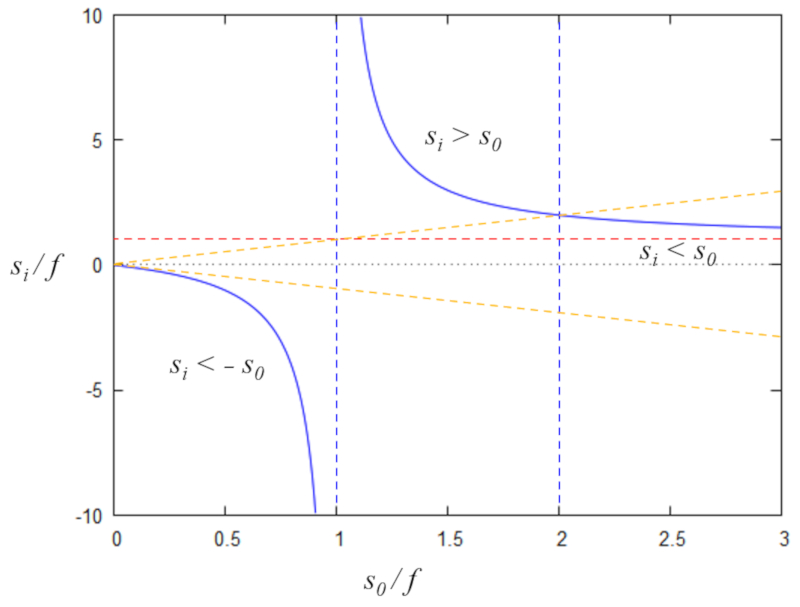
ID:(12699, 0)


Tamaño de la imagen
Exercise

Como la relación de los tamaño de la imagen se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{s_i}{s_o}$

\\n\\nCon la relación entre las posiciones\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\nla relación de tamaños se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{1}{1-s_o/f}$

\\n\\npor lo que con\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{a_i}{a_o}$

\\n\\nse puede escribir la relación\\n\\n

$y=\displaystyle\frac{1}{x-1}$



que se grafica como

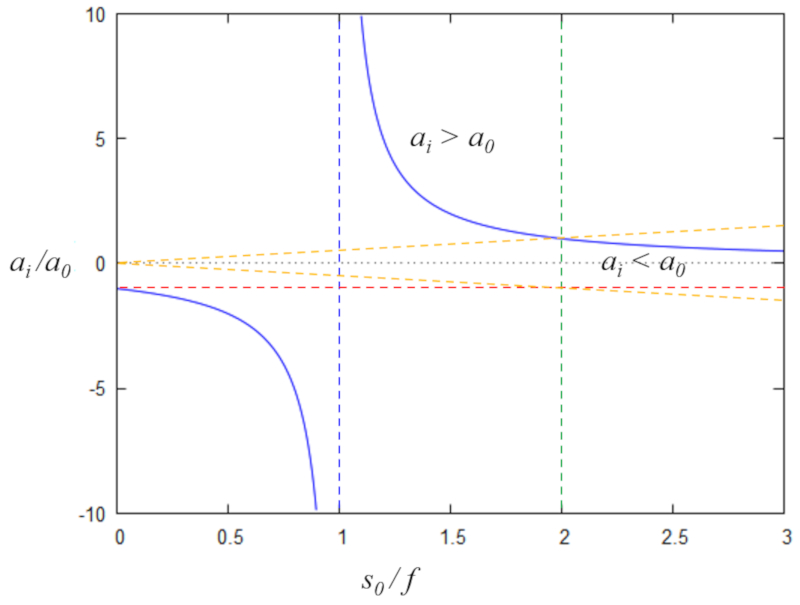
ID:(12700, 0)


Optical elements
Description

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$s_{lc}$
s_lc
Distancia de la imagen del lente cóncavo
m
$s_o$
s_o
Distancia del objeto al lente cóncavo
m
$f_{lc}$
f_lc
Foco del lente cóncavo
m
$a_o$
a_o
Object Size
m
$a_{lc}$
a_lc
Tamaño de la imagen en un lente cóncavo
m

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Una relaci n se puede armar con los tri ngulos del lado del objeto. En este caso la similitud nos permite escribir que el tama o del objeto a_o es a la distancia del objeto s_o al foco f es como el tama o de la imagen a_i es a la distancia del foco f:\\n\\n

$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$



Con la relaci n de similitud de los tri ngulos

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$



se puede mostrar que se cumple:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

(ID 3347)

Examples

In the case of a biconvex lens a beam that reaches the lens

- parallel to the optical axis is refracted by the focus
- via the focus is refracted parallel to the optical axis
- via the origin of the continuous optical axis in a straight line

what in the case of an object at a distance greater than the photo corresponds to:

(ID 1856)

Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os con posiciones

(ID 12697)

For any lens you can draw characteristic beams with which you can similarly show that the sizes of the object and the image are in the same proportion as their distances to the optical element (lens or mirror).

If the object has a size a_o, it is at a distance s_o of the lens, the image is a size a_i and is at a distance s_i, by similarity of the triangles it can be shown that

$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$

(ID 3346)

Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os, posici n del objeto y foco:

(ID 12698)

Por similitud de los tri ngulos de los tama os del objeto y la imagen y las posiciones del objeto y foco permite por similitud de tri ngulos mostrar que:

$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$

(ID 3347)

Como la relaci n entre el foco, posici n del objeto y posici n de la imagen esta dada por\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\ny se introduce las variables\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{s_i}{f}$

\\n\\nse puede escribir la relaci n\\n\\n

$y=\displaystyle\frac{x}{x-1}$



que se grafica como

(ID 12699)

Como la relaci n de los tama o de la imagen se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{s_i}{s_o}$

\\n\\nCon la relaci n entre las posiciones\\n\\n

$\displaystyle\frac{1}{f}=\displaystyle\frac{1}{s_o}+\displaystyle\frac{1}{s_i}$

\\n\\nla relaci n de tama os se puede escribir como\\n\\n

$\displaystyle\frac{a_i}{a_0}=\displaystyle\frac{1}{1-s_o/f}$

\\n\\npor lo que con\\n\\n

$x=\displaystyle\frac{s_o}{f}$

, y\\n\\n

$y=\displaystyle\frac{a_i}{a_o}$

\\n\\nse puede escribir la relaci n\\n\\n

$y=\displaystyle\frac{1}{x-1}$



que se grafica como

(ID 12700)

ID:(1667, 0)