Péndulo Físico
Storyboard 
En el caso de un péndulo compuesto de una masa real la energía potencial se da por el efecto de elevar el centro de masa contra el campo gravitacional a medida que el péndulo se desvía por un angulo dado.
ID:(1421, 0)
Péndulo Físico
Descripción 
En el caso de un péndulo compuesto con una masa real, la energía potencial se genera al elevar el centro de masa contra el campo gravitacional a medida que el péndulo se desvía por un ángulo determinado.
Variables
Cálculos
Cálculos
Ecuaciones
La variación del trabajo ($\Delta W$) necesaria para que un objeto cambie de la velocidad angular inicial ($\omega_0$) a la velocidad angular ($\omega$) se obtiene aplicando un el torque ($T$) que produce un desplazamiento angular la diferencia de ángulos ($\Delta\theta$), según:
| $ \Delta W = T \Delta\theta $ |
Aplicando la segunda ley de Newton para la rotación, en función de el momento de inercia para eje que no pasa por el CM ($I$) y la aceleración angular media ($\bar{\alpha}$):
| $ T = I \alpha $ |
esta expresión puede reescribirse como:
$\Delta W = I \alpha \Delta\theta$
o, utilizando la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
obtenemos:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Si utilizamos la definición de la velocidad angular media ($\bar{\omega}$) y el tiempo transcurrido ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
resulta:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
donde la diferencia de velocidades angulares ($\Delta\omega$) se expresa como:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Por otro lado, la velocidad angular puede aproximarse mediante la velocidad angular promedio:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Combinando ambas expresiones, se obtiene la ecuación:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Por lo tanto, el cambio en la energía se expresa como:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Lo que nos permite definir la energía cinética rotacional como:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 3687)
La energ a potencial gravitacional de un p ndulo con masa
| $ U = m g L (1-\cos \theta )$ |
donde
Para peque os ngulos, la funci n coseno se puede aproximar mediante la serie de Taylor hasta el segundo t rmino
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
lo que lleva a que la energ a potencial se reduce a
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
(ID 4514)
Dado que la la energía cinética de rotación ($K_r$) del péndulo físico, en función de el momento de inercia para eje que no pasa por el CM ($I$) y la velocidad angular ($\omega$), está representada por:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
y que la energía potencial del péndulo ($V$), en función de la masa gravitacional ($m_g$), el largo del péndulo ($L$), el angulo de oscilación ($\theta$) y la aceleración gravitacional ($g$), se expresa como:
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
La ecuación de la energía total se escribe como:
$E = \displaystyle\frac{1}{2}I\omega^2 + \displaystyle\frac{1}{2}mgl\theta^2$
Sabiendo que la período ($T$) se define como:
$T = 2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
Podemos determinar la frecuencia angular mediante:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
(ID 12338)
Utilizando el n mero complejo
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
introducido en
| $ \dot{z} = i \omega_0 z $ |
obtenemos
$\dot{z} = i\omega_0 z = i \omega_0 x_0 \cos \omega_0 t - \omega_0 x_0 \sin \omega_0 t$
por lo tanto, la velocidad se obtiene como la parte real
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
Ejemplos
(ID 15850)
A diferencia del péndulo matemático, el péndulo físico considera una la masa gravitacional ($m_g$) extendida en lugar de una masa puntual. Si bien el largo del péndulo ($L$) se define como la distancia entre el eje de giro y el centro de masa del cuerpo lo que hace que la energía potencial sea equivalente en ambos modelos, la la energía cinética de rotación ($K_r$) ya no puede aproximarse mediante expresiones que dependen únicamente de el largo del péndulo ($L$) y la masa gravitacional ($m_g$). En este caso, es imprescindible conocer el el momento de inercia para eje que no pasa por el CM ($I$) real del cuerpo para representar correctamente su comportamiento dinámico.
(ID 7097)
A diferencia del péndulo matemático, el péndulo físico considera una la masa gravitacional ($m_g$) extendida en lugar de una masa puntual. Al definir el largo del péndulo ($L$) como la distancia entre el eje de giro y el centro de masa del cuerpo, la la energía potencial del péndulo ($V$) resulta equivalente en ambos modelos. Sin embargo, la la energía cinética de rotación ($K_r$) ya no puede aproximarse mediante la expresión que depende únicamente de el largo del péndulo ($L$) y la masa gravitacional ($m_g$), sino que requiere incorporar el momento de inercia para eje que no pasa por el CM ($I$) del cuerpo para representar adecuadamente su distribución de masa.
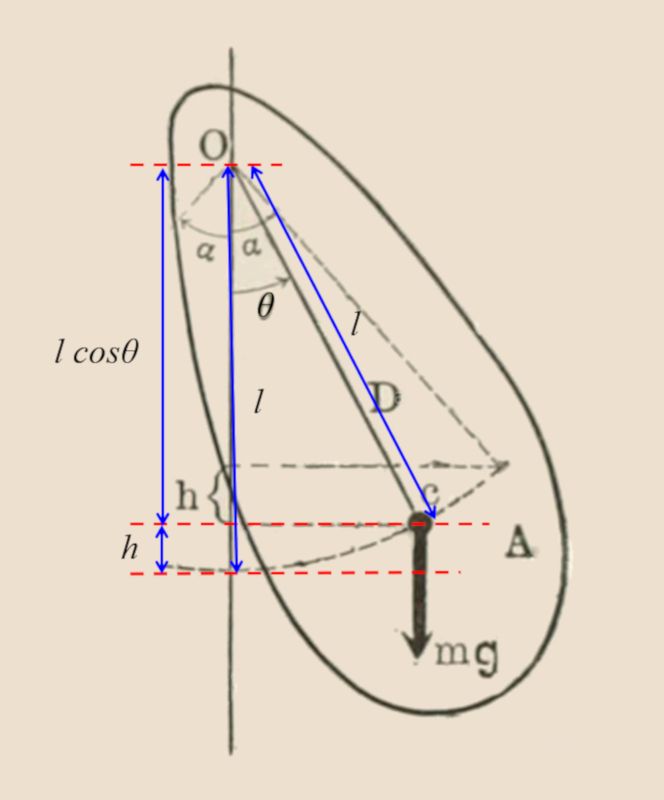
(ID 1188)
(ID 15853)
La energía total ($E$) corresponde a la suma de la energía cinética total ($K$) y la energía potencial ($V$):
| $ E = K + V $ |
(ID 3687)
La energía cinética de rotación ($K_r$) es una función de la velocidad angular ($\omega$) y de una medida de la inercia representada por el momento de inercia para eje que no pasa por el CM ($I$):
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
La energ a potencial gravitacional de un p ndulo es
| $ U = m g L (1-\cos \theta )$ |
que para ngulos peque os puede aproximarse como:
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
Es importante destacar que el ngulo debe estar expresado en radianes.
(ID 4514)
La frecuencia angular del péndulo físico ($\omega_0$) se determina en función de la masa gravitacional ($m_g$), el largo del péndulo ($L$), el momento de inercia para eje que no pasa por el CM ($I$) y la aceleración gravitacional ($g$):
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
La relación entre la frecuencia angular ($\omega$) y la frecuencia del sonido ($\nu$) se expresa como:
| $ \omega = 2 \pi \nu $ |
(ID 12338)
La frecuencia angular ($\omega$) es con la período ($T$) igual a
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
(ID 12335)
La frecuencia del sonido ($\nu$) representa la cantidad de oscilaciones que ocurren en un segundo. Mientras tanto, la período ($T$) es el tiempo que tarda una sola oscilaci n. Por lo tanto, el n mero de oscilaciones por segundo es:
| $ \nu =\displaystyle\frac{1}{ T }$ |
La frecuencia se expresa en Hertz (Hz).
(ID 4427)
Con la descripci n de la oscilaci n usando
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
la parte real corresponde a la evoluci n temporal de la amplitud
| $ x = x_0 \cos \omega_0 t $ |
(ID 14074)
Al obtener la parte real de la derivada del n mero complejo que representa la oscilaci n
| $ \dot{z} = i \omega_0 z $ |
cuya parte real se refiere a la velocidad
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
ID:(1421, 0)
