Pêndulo físico
Descrição 
No caso de um pêndulo composto com uma massa real, a energia potencial é gerada ao elevar o centro de massa contra o campo gravitacional à medida que o pêndulo se desvia por um determinado ângulo.
Variáveis
Cálculos
Cálculos
Equações
La variação de trabalho ($\Delta W$) necessária para que um objeto mude de la velocidade angular inicial ($\omega_0$) para la velocidade angular ($\omega$) é obtida aplicando um la torque ($T$) que gera um deslocamento angular la diferença de ângulos ($\Delta\theta$), de acordo com:
| $ \Delta W = T \Delta\theta $ |
Aplicando a segunda lei de Newton para rotação, em função de la momento de inércia do eixo que não passa pelo CM ($I$) e la aceleração angular média ($\bar{\alpha}$):
| $ T = I \alpha $ |
essa expressão pode ser reescrita como:
$\Delta W = I \alpha \Delta\theta$
ou, utilizando la diferença de velocidades angulares ($\Delta\omega$) e o tempo decorrido ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
temos:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Utilizando a definição de la velocidade angular média ($\bar{\omega}$) e o tempo decorrido ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
obtém-se:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
onde la diferença de velocidades angulares ($\Delta\omega$) é expresso como:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
Por outro lado, a velocidade angular pode ser aproximada pela velocidade angular média:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
Combinando ambas as expressões, obtemos:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Assim, a variação da energia é expressa como:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
Isso nos permite definir a energia cinética de rotação como:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 3687)
A energia potencial gravitacional de um p ndulo com massa
| $ U = m g L (1-\cos \theta )$ |
onde
Para ngulos pequenos, a fun o cosseno pode ser aproximada pela expans o em s rie de Taylor at a segunda ordem
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
Essa aproxima o resulta em uma simplifica o da energia potencial para
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
(ID 4514)
Dado que la energia cinética rotacional ($K_r$) do pêndulo físico, em função de la momento de inércia do eixo que não passa pelo CM ($I$) e la velocidade angular ($\omega$), é representado por:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
e que la energia potencial do pêndulo ($V$), em função de la massa gravitacional ($m_g$), la comprimento do pêndulo ($L$), la ângulo de balanço ($\theta$) e la aceleração gravitacional ($g$), é expressa como:
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
A equação da energia total é escrita como:
$E = \displaystyle\frac{1}{2}I\omega^2 + \displaystyle\frac{1}{2}mgl\theta^2$
Sabendo que la período ($T$) é definido como:
$T = 2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
Podemos determinar a frequência angular como:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
(ID 12338)
Usando o n mero complexo
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
introduzido em
| $ \dot{z} = i \omega_0 z $ |
obtemos
$\dot{z} = i\omega_0 z = i \omega_0 x_0 \cos \omega_0 t - \omega_0 x_0 \sin \omega_0 t$
assim, a velocidade obtida como a parte real
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
Exemplos
(ID 15850)
Ao contrário do pêndulo matemático, o pêndulo físico considera uma la massa gravitacional ($m_g$) estendida em vez de uma massa pontual. Embora la comprimento do pêndulo ($L$) seja definido como a distância entre o eixo de rotação e o centro de massa do corpo o que faz com que a energia potencial seja equivalente em ambos os modelos , la energia cinética rotacional ($K_r$) já não pode ser aproximado utilizando expressões que dependem apenas de la comprimento do pêndulo ($L$) e la massa gravitacional ($m_g$). Neste caso, é essencial conhecer o la momento de inércia do eixo que não passa pelo CM ($I$) real do corpo para representar corretamente o seu comportamento dinâmico.
(ID 7097)
Ao contrário do pêndulo matemático, o pêndulo físico considera uma la massa gravitacional ($m_g$) estendida em vez de uma massa pontual. Ao definir la comprimento do pêndulo ($L$) como a distância entre o eixo de rotação e o centro de massa do corpo, la energia potencial do pêndulo ($V$) é a mesma em ambos os modelos. No entanto, la energia cinética rotacional ($K_r$) já não pode ser aproximada pela expressão que depende apenas de la comprimento do pêndulo ($L$) e la massa gravitacional ($m_g$); é necessário incluir la momento de inércia do eixo que não passa pelo CM ($I$) do corpo para representar corretamente a distribuição de massa.
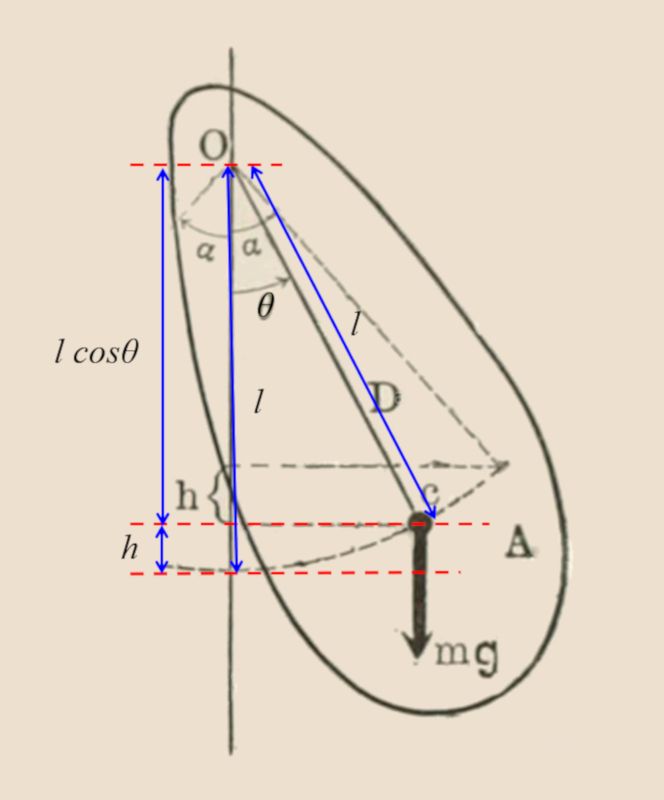
(ID 1188)
(ID 15853)
La energia total ($E$) corresponde à soma de la energia cinética total ($K$) e la energia potencial ($V$):
| $ E = K + V $ |
(ID 3687)
La energia cinética rotacional ($K_r$) é uma função de la velocidade angular ($\omega$) e de uma medida de inércia representada por la momento de inércia do eixo que não passa pelo CM ($I$):
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
A energia potencial gravitacional de um p ndulo
| $ U = m g L (1-\cos \theta )$ |
que pode ser aproximada para ngulos pequenos como:
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
importante observar que o ngulo deve estar em radianos.
(ID 4514)
La frequência angular do pêndulo físico ($\omega_0$) é determinado em função de la massa gravitacional ($m_g$), la comprimento do pêndulo ($L$), la momento de inércia do eixo que não passa pelo CM ($I$) e la aceleração gravitacional ($g$):
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
A relação entre la frequência angular ($\omega$) e la frequência do som ($\nu$) é expressa como:
| $ \omega = 2 \pi \nu $ |
(ID 12338)
La frequência angular ($\omega$) com la período ($T$) igual a
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
(ID 12335)
La frequência do som ($\nu$) corresponde ao n mero de vezes que ocorre uma oscila o em um segundo. J La período ($T$) o tempo que uma nica oscila o leva. Portanto, o n mero de oscila es por segundo :
| $ \nu =\displaystyle\frac{1}{ T }$ |
A frequ ncia indicada em Hertz (Hz).
(ID 4427)
Com a descri o da oscila o usando
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
a parte real corresponde evolu o temporal da amplitude
| $ x = x_0 \cos \omega_0 t $ |
(ID 14074)
Ao obtermos a parte real da derivada do n mero complexo que representa a oscila o
| $ \dot{z} = i \omega_0 z $ |
cuja parte real corresponde velocidade
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
ID:(1421, 0)
