Osciladores en el espacio de fase
Storyboard 
Existen distintos tipos de osciladores, siendo los más estudiados el oscilador de resorte y el péndulo. Ambos son fundamentales para comprender aspectos clave del movimiento humano, como la marcha.Por un lado, los músculos pueden comportarse de manera análoga a un resorte, almacenando y liberando energía elástica durante el movimiento. Por otro lado, al desplazarnos, ciertos sistemas del cuerpo, como los brazos, funcionan como osciladores que realizan un trabajo compensatorio, oscilando a la misma frecuencia que nuestros pasos para mantener el equilibrio y optimizar la dinámica del movimiento.En el caso del péndulo, se distinguen dos tipos: el péndulo matemático, que modela la oscilación de una masa puntual suspendida de un hilo sin masa, y el péndulo físico, que considera la distribución de masa y la geometría del objeto real.
ID:(51, 0)
Representación de la elipse
Descripción 
En el espacio de fase la oscilación se puede representar por una elipse
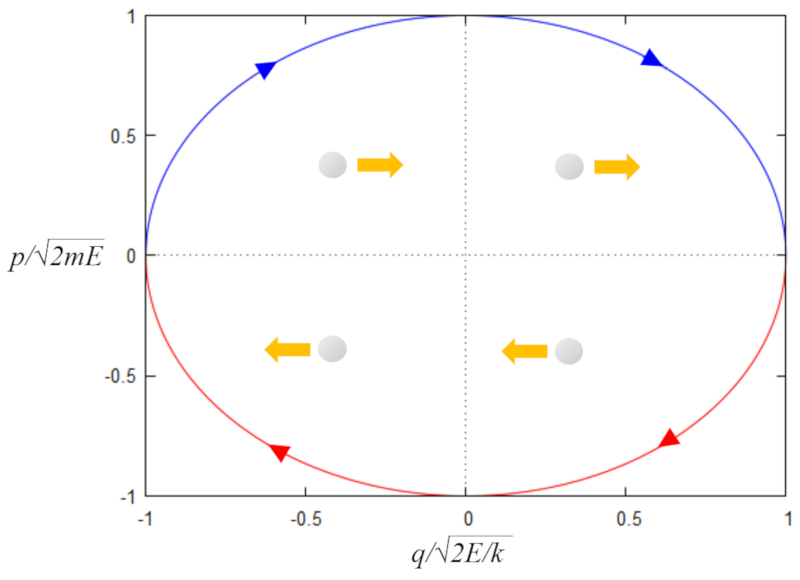
\\n \\nque en forma matemática se escribe como\\n\\n
$\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1$
\\n\\nde semiejes
$x=a\cos u$
\\n\\ny\\n\\n
$y=b\sin u$
ID:(7105, 0)
Osciladores en el espacio de fase
Modelo 
Existen distintos tipos de osciladores siendo los mas discutidos el cerrado por un resorte y el péndulo. Ambos son relevantes para estudiar como caminamos. Por un lado esta el comportamiento similar a un resorte que son capaces de mostrar los músculos. Por otro lado, al desplazarnos, existen sistemas como los brazos que realizan un trabajo compensatorio oscilando con la misma frecuencia de nuestros pasos. En el caso del péndulo existen dos tipos, el matemático que considera la oscilación de una masa puntual y el físico que considera la forma del objeto como tal.
Variables
Cálculos
Cálculos
Ecuaciones
(ID 12338)
Ejemplos
(ID 16244)
En el espacio de fases, la oscilación se representa mediante una elipse:

Su expresión matemática general es:
$\displaystyle\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
donde los parámetros $a$ y $b$ corresponden a los semiejes mayor y menor, respectivamente.
Esta trayectoria también puede describirse de forma paramétrica mediante un parámetro $u$, que varía de $0$ a $2\pi$, utilizando funciones trigonométricas:
$x = a \cos u$
y
$y = b \sin u$
(ID 7105)
En el caso de un resorte, la energía total la energía del resorte ($E$), que se conserva, está compuesta por el trabajo inicial ($W_0$), asociada a la masa inercial ($m_i$) y la velocidad ($v$):
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
La la energía potencial ($V$) del resorte está relacionada con la constante de Hooke ($k$) y la posición ($x$):
| $ V =\displaystyle\frac{1}{2} k x ^2$ |
De manera que la energía total la energía del resorte ($E$) se expresa como:
$E_k=\displaystyle\frac{1}{2}m_iv^2+\displaystyle\frac{1}{2}kx^2$
Si se reescribe esta expresión como:
| $\displaystyle\frac{ v ^2}{\displaystyle\frac{2 E }{ m_i }}+\displaystyle\frac{ x ^2}{\displaystyle\frac{2 E }{ k }}=1$ |
se puede observar que corresponde a una elipse en el espacio velocidad la velocidad ($v$) y elongación la posición ($x$), cuyos semiejes son:
$a=\sqrt{\displaystyle\frac{2E_k}{k}}=x_0$
, y
$b=\sqrt{\displaystyle\frac{2E_k}{m_i}}=v_0$
.Los semiejes corresponden, respectivamente, a la amplitud máxima
(ID 16238)
En el caso de la amplitud, que corresponde a nuestra coordenada la posición ($x$), el semieje depende de la energía del resorte ($E$) y la constante de Hooke ($k$):
$a=\sqrt{\displaystyle\frac{2E_k}{k}}$
Además, el tiempo ($t$) se escala con la período ($T$):
$u=\displaystyle\frac{2\pi t}{T}$
Por lo tanto, la amplitud se expresa como:
| $ x =\sqrt{\displaystyle\frac{2 E }{ k }}\cos \displaystyle\frac{2 \pi t }{ T }$ |
(ID 16239)
En el caso de la amplitud, que corresponde a nuestra coordenada la velocidad ($v$), el semieje depende de la energía del resorte ($E$) y la masa inercial ($m_i$):
$b=\sqrt{\displaystyle\frac{2E}{m}}$
Asimismo, el tiempo ($t$) se escala con la período ($T$):
$u=\displaystyle\frac{2\pi t}{T}$
Por lo tanto, la amplitud se expresa como:
| $ v =-\sqrt{\displaystyle\frac{2 E }{ m_i }}\sin \displaystyle\frac{2 \pi t }{ T }$ |
(ID 16240)
Dado que la frecuencia angular ($\omega$), junto con la período ($T$), es igual a:
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
y que la frecuencia del sonido ($\nu$) es igual a:
| $ \nu =\displaystyle\frac{1}{ T }$ |
se cumple que:
| $ \omega = 2 \pi \nu $ |
(ID 16242)
Dado que la oscilación obedece las leyes físicas, es posible utilizar el hecho de que el área bajo la curva la velocidad ($v$) en función de el tiempo ($t$) corresponde al camino recorrido, lo que permite determinar el período. Como la velocidad ($v$) depende de la energía del resorte ($E$), la masa inercial ($m_i$) y la período ($T$):
$\displaystyle\int_0^{T/2}v(t)dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\int_0^{T/2}\cos \displaystyle\frac{2\pi t}{T}dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\frac{T}{\pi}$
El camino entre un mínimo y un máximo de elongación es decir, entre los instantes
$x_{max}-x_{min}=2\sqrt{\displaystyle\frac{2E}{k}}$
Por lo tanto, se cumple que:
| $ T =2 \pi \sqrt{\displaystyle\frac{ m_i }{ k }}$ |
(ID 16241)
(ID 16243)
ID:(51, 0)
