Physical Pendulum
Storyboard 
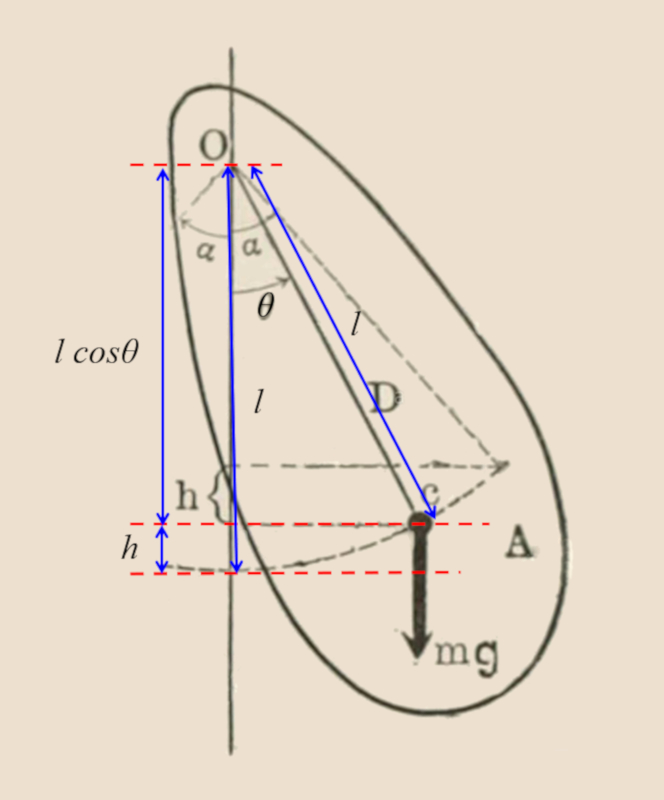
In the case of a pendulum composed of a real mass the potential energy is given by the effect of raising the center of mass against the gravitational field as the pendulum deviates by a given angle.
ID:(1421, 0)
Physical Pendulum
Description 
In the case of a compound pendulum with a real mass, the potential energy is generated by raising the center of mass against the gravitational field as the pendulum deviates by a given angle.
Variables
Calculations
Calculations
Equations
The work variance ($\Delta W$) required for an object to change from the initial Angular Speed ($\omega_0$) to the angular Speed ($\omega$) is obtained by applying a the torque ($T$) that produces an angular displacement the difference of Angles ($\Delta\theta$), according to:
| $ \Delta W = T \Delta\theta $ |
Applying Newton's second law for rotation, in terms of the moment of inertia for axis that does not pass through the CM ($I$) and the mean Angular Acceleration ($\bar{\alpha}$):
| $ T = I \alpha $ |
this expression can be rewritten as:
$\Delta W = I \alpha \Delta\theta$
or, using the difference in Angular Speeds ($\Delta\omega$) and the time elapsed ($\Delta t$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
we get:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta$
Using the definition of the mean angular velocity ($\bar{\omega}$) and the time elapsed ($\Delta t$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
results in:
$\Delta W = I\displaystyle\frac{\Delta\omega}{\Delta t} \Delta\theta = I\omega \Delta\omega$
where the difference in Angular Speeds ($\Delta\omega$) is expressed as:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
On the other hand, the angular velocity can be approximated by the average angular velocity:
$\bar{\omega}=\displaystyle\frac{\omega_1 + \oemga_2}{2}$
By combining both expressions, we obtain the equation:
$\Delta W = I \omega \Delta\omega = I(\omega_2 - \omega_1) \displaystyle\frac{(\omega_1 + \omega_2)}{2} = \displaystyle\frac{I}{2}(\omega_2^2 - \omega_1^2)$
Therefore, the change in energy is expressed as:
$\Delta W = \displaystyle\frac{I}{2}\omega_2^2 - \displaystyle\frac{I}{2}\omega_1^2$
This allows us to define the rotational kinetic energy as:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
(ID 3687)
The gravitational potential energy of a pendulum with mass
| $ U = m g L (1-\cos \theta )$ |
where
For small angles, the cosine function can be approximated using a Taylor series expansion up to the second term
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
This approximation leads to the simplification of the potential energy to
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
(ID 4514)
Given that the the kinetic energy of rotation ($K_r$) of the physical pendulum, in terms of the moment of inertia for axis that does not pass through the CM ($I$) and the angular Speed ($\omega$), is represented by:
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
and that the potential Energy Pendulum ($V$), as a function of the gravitational mass ($m_g$), the pendulum Length ($L$), the swing angle ($\theta$) and the gravitational Acceleration ($g$), is expressed as:
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
The total energy equation is written as:
$E = \displaystyle\frac{1}{2}I\omega^2 + \displaystyle\frac{1}{2}mgl\theta^2$
Knowing that the period ($T$) is defined as:
$T = 2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
We can determine the angular frequency as:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
(ID 12338)
Using the complex number
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
introduced in
| $ \dot{z} = i \omega_0 z $ |
we obtain
$\dot{z} = i\omega_0 z = i \omega_0 x_0 \cos \omega_0 t - \omega_0 x_0 \sin \omega_0 t$
thus, the velocity is obtained as the real part
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
Examples
(ID 15850)
Unlike the mathematical pendulum, the physical pendulum considers an extended the gravitational mass ($m_g$) instead of a point mass. While the pendulum Length ($L$) is defined as the distance between the axis of rotation and the center of mass of the body which makes the potential energy equivalent in both models the kinetic energy of rotation ($K_r$) can no longer be approximated using expressions that depend only on the pendulum Length ($L$) and the gravitational mass ($m_g$). In this case, it is essential to know the actual the moment of inertia for axis that does not pass through the CM ($I$) of the body to correctly represent its dynamic behavior.
(ID 7097)
Unlike the mathematical pendulum, the physical pendulum considers an extended the gravitational mass ($m_g$) instead of a point mass. When defining the pendulum Length ($L$) as the distance between the axis of rotation and the center of mass of the body, the potential Energy Pendulum ($V$) is the same for both models. However, the kinetic energy of rotation ($K_r$) can no longer be approximated using the expression that depends only on the pendulum Length ($L$) and the gravitational mass ($m_g$); it must include the moment of inertia for axis that does not pass through the CM ($I$) of the body to properly account for the mass distribution.
(ID 1188)
(ID 15853)
The total Energy ($E$) corresponds to the sum of the total Kinetic Energy ($K$) and the potential Energy ($V$):
| $ E = K + V $ |
(ID 3687)
The kinetic energy of rotation ($K_r$) is a function of the angular Speed ($\omega$) and of a measure of inertia represented by the moment of inertia for axis that does not pass through the CM ($I$):
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
(ID 3255)
The gravitational potential energy of a pendulum is
| $ U = m g L (1-\cos \theta )$ |
which for small angles can be approximated as:
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
It's important to note that the angle must be expressed in radians.
(ID 4514)
The angular Frequency of Physical Pendulum ($\omega_0$) is determined as a function of the gravitational mass ($m_g$), the pendulum Length ($L$), the moment of inertia for axis that does not pass through the CM ($I$), and the gravitational Acceleration ($g$):
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
(ID 4517)
The relationship between the angular frequency ($\omega$) and the sound frequency ($\nu$) is expressed as:
| $ \omega = 2 \pi \nu $ |
(ID 12338)
The angular frequency ($\omega$) is with the period ($T$) equal to
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
(ID 12335)
The sound frequency ($\nu$) corresponds to the number of times an oscillation occurs within one second. The period ($T$) represents the time it takes for one oscillation to occur. Therefore, the number of oscillations per second is:
| $ \nu =\displaystyle\frac{1}{ T }$ |
Frequency is indicated in Hertz (Hz).
(ID 4427)
With the description of the oscillation using
| $ z = x_0 \cos \omega_0 t + i x_0 \sin \omega_0 t $ |
the real part corresponds to the temporal evolution of the amplitude
| $ x = x_0 \cos \omega_0 t $ |
(ID 14074)
When we extract the real part of the derivative of the complex number representing the oscillation
| $ \dot{z} = i \omega_0 z $ |
whose real part corresponds to the velocity
| $ v = - x_0 \omega_0 \sin \omega_0 t $ |
(ID 14076)
ID:(1421, 0)
