Utilisateur:
Énergie potentielle d'un pendule mathématique pour les petits angles
Équation 
L'énergie potentielle gravitationnelle d'un pendule est
| $ U = m g L (1-\cos \theta )$ |
qui peut être approximée pour de petits angles comme :
 $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
L'énergie potentielle gravitationnelle d'un pendule avec une masse
| $ U = m g L (1-\cos \theta )$ |
où
Pour de petits angles, la fonction cosinus peut être approximée par le développement en série de Taylor jusqu'à l'ordre deux
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
Cette approximation conduit à une simplification de l'énergie potentielle en
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
Il est important de noter que l'angle doit être en radians.
ID:(4514, 0)
Énergie cinétique de rotation
Équation
Dans le cas de l'étude de la translation, la définition de l'énergie
| $ \Delta W = T \Delta\theta $ |
est appliquée à la deuxième loi de Newton
| $ T = I \alpha $ |
ce qui conduit à l'expression
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
L'énergie nécessaire pour qu'un objet passe de la vitesse angulaire $\omega_1$ à la vitesse angulaire $\omega_2$ peut être calculée à l'aide de la définition
| $ \Delta W = T \Delta\theta $ |
Avec la deuxième loi de Newton, nous pouvons réécrire cette expression comme
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
En utilisant la définition de la vitesse angulaire
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
nous obtenons
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I,\omega,\Delta\omega$
La différence entre les vitesses angulaires est
$\Delta\omega=\omega_2-\omega_1$
D'autre part, la vitesse angulaire elle-même peut être approximée par la vitesse angulaire moyenne
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
En utilisant ces deux expressions, nous obtenons l'équation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Ainsi, l'énergie varie selon
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Nous pouvons utiliser cela pour définir l'énergie cinétique
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Fréquence angulaire pour un pendule physique
Équation
En ce qui concerne le pendule physique:
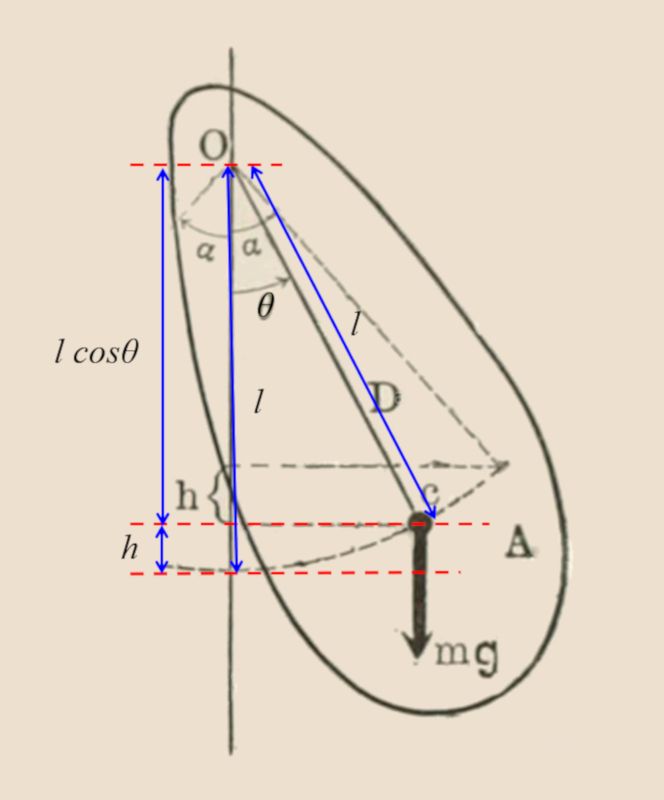
L'énergie est donnée par :
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Par conséquent, la fréquence angulaire est:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
Étant donné que l'énergie cinétique du pendule physique avec un moment d'inertie $I$ et une vitesse angulaire $\omega$ est représentée par
et l'énergie potentielle gravitationnelle est donnée par
où $m$ est la masse, $l$ est la longueur de la corde, $\theta$ est l'angle et $g$ est l'accélération angulaire, l'équation d'énergie peut être exprimée comme
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Comme la période est définie comme
$T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
nous pouvons déterminer la fréquence angulaire comme suit :
ID:(4517, 0)
0
Video
Vidéo: Pendule physique