User:
Physical Pendulum
Storyboard 
In the case of a pendulum composed of a real mass the potential energy is given by the effect of raising the center of mass against the gravitational field as the pendulum deviates by a given angle.
ID:(1421, 0)
Potential energy of a mathematical pendulum for small angles
Equation
The gravitational potential energy of a pendulum is
| $ U = m g L (1-\cos \theta )$ |
which for small angles can be approximated as:
 $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
The gravitational potential energy of a pendulum with mass
| $ U = m g L (1-\cos \theta )$ |
where
For small angles, the cosine function can be approximated using a Taylor series expansion up to the second term
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
This approximation leads to the simplification of the potential energy to
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
It's important to note that the angle must be expressed in radians.
ID:(4514, 0)
Kinetic Energy of Rotation
Equation
In the case being studied of translational motion, the definition of energy
| $ \Delta W = T \Delta\theta $ |
is applied to Newton's second law
| $ T = I \alpha $ |
resulting in the expression
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
The energy required for an object to change its angular velocity from $\omega_1$ to $\omega_2$ can be calculated using the definition
| $ \Delta W = T \Delta\theta $ |
Applying Newton's second law, this expression can be rewritten as
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Using the definition of angular velocity
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
we get
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
The difference in angular velocities is
$\Delta\omega=\omega_2-\omega_1$
On the other hand, angular velocity itself can be approximated with the average angular velocity
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Using both expressions, we obtain the equation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Thus, the change in energy is given by
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
This allows us to define kinetic energy as
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Angular frequency for a physical pendulum
Equation
Regarding the physical pendulum:
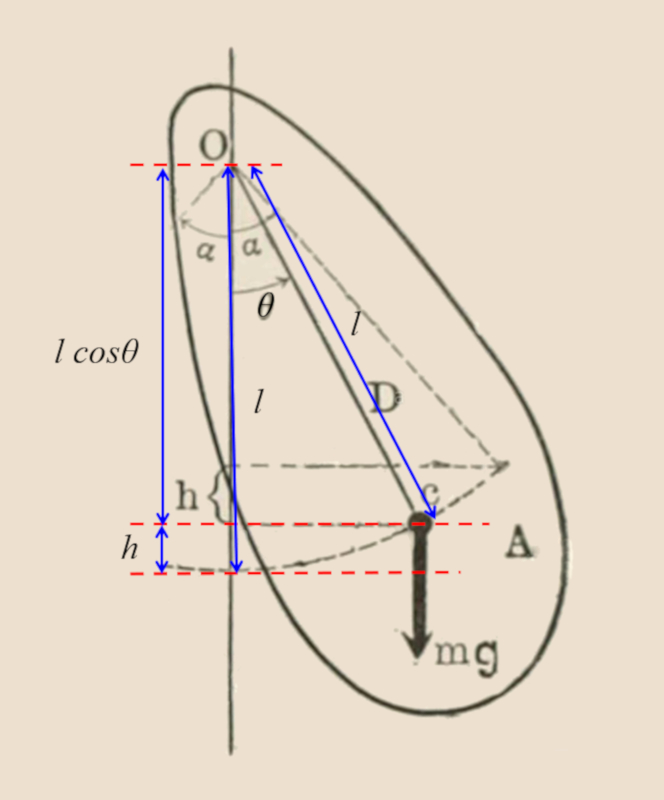
The energy is given by:
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
As a result, the angular frequency is:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
Given that the kinetic energy of the physical pendulum with moment of inertia $I$ and angular velocity $\omega$ is represented by
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
and the gravitational potential energy is given by
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
where $m$ is mass, $l$ is string length, $\theta$ is the angle, and $g$ is angular acceleration, the energy equation can be expressed as
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
As the period is defined as
$T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
we can determine the angular frequency as
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
ID:(4517, 0)
0
Video
Video: Physical Pendulum