Usuario:
Péndulo Físico
Storyboard 
En el caso de un péndulo compuesto de una masa real la energía potencial se da por el efecto de elevar el centro de masa contra el campo gravitacional a medida que el péndulo se desvía por un angulo dado.
ID:(1421, 0)
Energía potencial de un péndulo matemático para pequeños ángulos
Ecuación
La energía potencial gravitacional de un péndulo es
| $ U = m g L (1-\cos \theta )$ |
que para ángulos pequeños puede aproximarse como:
 $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
La energía potencial gravitacional de un péndulo con masa
| $ U = m g L (1-\cos \theta )$ |
donde
Para pequeños ángulos, la función coseno se puede aproximar mediante la serie de Taylor hasta el segundo término
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
lo que lleva a que la energía potencial se reduce a
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
Es importante destacar que el ángulo debe estar expresado en radianes.
ID:(4514, 0)
Energía cinética de rotación
Ecuación
En el caso de estudio de la translación, la definición de la energía
| $ \Delta W = T \Delta\theta $ |
se aplica al segundo principio de Newton
| $ T = I \alpha $ |
lo que nos lleva a la expresión
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
La energía necesaria para que un objeto cambie su velocidad angular de $\omega_1$ a $\omega_2$ se puede calcular utilizando la definición
| $ \Delta W = T \Delta\theta $ |
Aplicando la segunda ley de Newton, esta expresión se puede reescribir como
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Utilizando la definición de velocidad angular
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
obtenemos
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
La diferencia en las velocidades angulares es
$\Delta\omega=\omega_2-\omega_1$
Por otro lado, la velocidad angular en sí se puede aproximar con la velocidad angular promedio
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Utilizando ambas expresiones, obtenemos la ecuación
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Así, el cambio en la energía está dado por
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Esto nos permite definir la energía cinética como
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Frecuencia angular para un péndulo físico
Ecuación
En relación al péndulo físico:
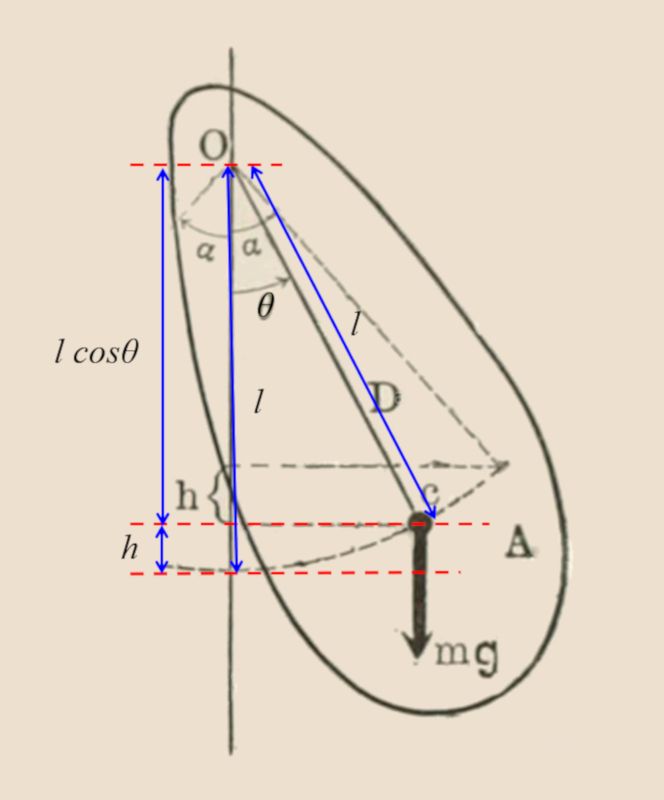
La energía se expresa como:
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Consecuentemente, la frecuencia angular es:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
Dado que la energía cinética del péndulo físico con momento de inercia $I$ y velocidad angular $\omega$ está representada por
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
y la energía potencial gravitacional está dada por
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
donde $m$ es la masa, $l$ es la longitud de la cuerda, $\theta$ es el ángulo y $g$ es la aceleración angular, la ecuación de energía se expresa como
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Dado que el período se define como
$T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
podemos determinar la frecuencia angular como
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
ID:(4517, 0)
0
Video
Video: Péndulo físico