Utilisateur:
Énergie cinétique en fonction du moment
Équation 
L'énergie cinétique d'une masse $m$
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
peut être exprimée en fonction du moment comme
 $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
Comme l'énergie cinétique est égale à
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
et le moment est
| $ p = m_i v $ |
nous pouvons l'exprimer comme
$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$
c'est-à-dire
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
ID:(4425, 0)
Oscillateur harmonique (ressort) représentant $p-q$
Équation
Pour le cas d'une masse oscillant avec un ressort, l'énergie en fonction du moment $p$ et de la position $q$ est
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
L'énergie cinétique en fonction du moment est
| $ K =\displaystyle\frac{ p ^2}{2 m_i }$ |
et l'énergie potentielle en fonction de la hauteur est
donc si l'on exprime l'allongement comme la position
$x = q$
nous obtenons
| $ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$ |
L'équation peut être écrite sous forme adimensionnelle comme
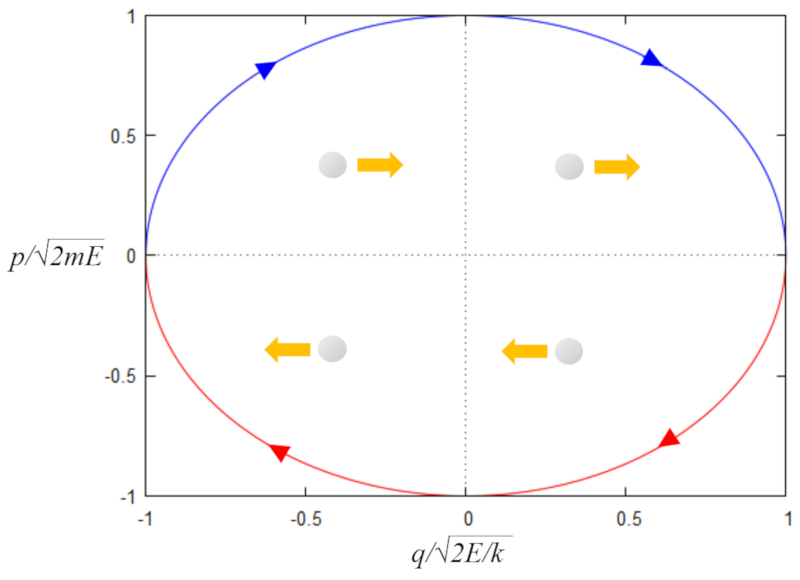
$1=y^2 + x^2$
avec
$x=\displaystyle\frac{q}{\sqrt{2E/k}}$
, et
$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$
lorsqu'elle est résolue pour
$y=\pm\sqrt{1-x^2}$
Sa représentation dans le plan xy est montrée ci-dessous
ID:(1187, 0)
Oscillations avec un ressort
Équation
L'un des systèmes qu'il illustre est celui d'un ressort. Celui-ci est associé à la déformation élastique du matériau à partir duquel le ressort est fabriqué. Lorsque nous parlons d'une déformation "élastique", nous entendons une déformation qui, lorsqu'on retire la contrainte appliquée, permet au système de retrouver complètement sa forme originale. Il est entendu qu'il ne subit pas de déformation plastique.
Étant donné que l'énergie du ressort est donnée par
$E=\displaystyle\frac{1}{2}m_i v^2+\displaystyle\frac{1}{2}k x^2$
le période sera égale à
$T=2\pi\sqrt{\displaystyle\frac{m_i}{k}}$
et donc, la fréquence angulaire est
| $ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$ |
Étant donné que l'énergie cinétique dépend de la masse $m$ et de la vitesse $v$, elle est donnée par
et l'énergie potentielle du ressort, qui dépend de la constante de raideur $k$ et de l'allongement $x$, est donnée par
Ainsi, l'énergie totale s'exprime comme
$E=\displaystyle\frac{1}{2}m_i v^2+\displaystyle\frac{1}{2}k x^2$
Comme la période est
$T=2\pi\sqrt{\displaystyle\frac{m_i}{k}}$
nous pouvons calculer la fréquence angulaire comme
$\omega_0=\displaystyle\frac{2\pi}{T}=\sqrt{\displaystyle\frac{k}{m_i}}$
ce qui implique
ID:(1242, 0)
0
Video
Vidéo: Oscillateurs sur un ressort